Fundamentals of Moment of Inertia

The moment of inertia can be derived as getting the moment of inertia of the parts and applying the transfer formula: I = I₀ + Ad². We have a comprehensive article explaining the approach to solving the moment of inertia.

Fundamentally, the moment of inertia is the second moment of area, which can be expressed as the following:

[math] I_{x}=\int \int y^{2}dA [math] [math] I_{y}=\int \int x^{2}dA [math]

To observe the derivation of the formulas below, we try to find the moment of inertia of an object such as a rectangle about its major axis using just the formula above. To get the moment of inertia, the limits have to be determined such that they are taken from the axis of rotation to its extreme fiber. This would be the limits of the outer integral. The inner integral has a limit from 0 to b. That said, we can also express dA as xdy, which will become bdy. As the axis of rotation is at the neutral axis, the moment of inertia can be integrated with an upper limit of h/2 and a lower limit of 0 and multiplied twice due to the symmetry of the rectangle. This leaves us with the integral below.

[math] I_{x}=2\int_{0}^{\frac{h}{2}} y^{2}bdy [math] Integrating, [math] I_{x}=2b \left [ \frac{y^{3}}{3} \right ]_{0}^{\frac{h}{2}} [math] [math] I_{x}=2b \left [ \frac{h^{3}}{24}-0 \right ] [math] [math] I_{x}=\frac{bh^{3}}{12} [math]

Moment of Inertia Formula for Beam Sections

SkyCiv has compiled a summary of moment of inertia equations for beam sections (second moment of area). Moment of inertia equations is extremely useful for fast and accurate calculations. The formulas have been summarised into their simplest forms for your convenience. SkyCiv also offers a Free Moment of Inertia Calculator for quick calculations or to check you have applied the formula correctly. The moment of inertia formula for rectangle, circle, hollow and triangle beam sections have been given. Some important things to remember regarding a beam’s area moment of inertia are:

• Area moment of inertia is different from the mass moment of inertia
• It is also known as the second moment of area
• It is a significant factor of deflection (the greater the I_x, the lower deflection will be)
• The units are in length to the power of 4
• The below equations give the moment of inertia with respect to the centroid of the section

REFERENCE	Ixx	Iyy
Moment of Inertia Equation for Rectangle or Rectangular Sections
	[math] \dfrac{bh^3}{12} [math]	[math] \dfrac{b^{3}h}{12} [math]
Moment of Inertia Equation for a Hollow Rectangular Section
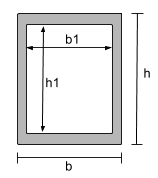	[math] \dfrac{bh^3}{12} – \dfrac{b_1h_1^3}{12} [math]	[math] \dfrac{b^3h}{12} – \dfrac{b_1^3h_1}{12} [math]
Moment of Inertia Equation for a Circle or Circular Section
	[math] \dfrac{\pi}{64}D^4 [math]	[math] \dfrac{\pi}{64}D^4 [math]
Moment of Inertia Equation for a Hollow Circular Section
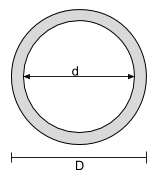	[math] \dfrac{\pi}{64}D^4 – \dfrac{\pi}{64}d^4 [math]	[math] \dfrac{\pi}{64}D^4 – \dfrac{\pi}{64}d^4 [math]
Moment of Inertia Equation for a Isosceles Triangle
	[math] \dfrac{bh^3}{36} [math]	[math] \dfrac{3b^3h}{144} [math]
Moment of Inertia Equation of an I-Section
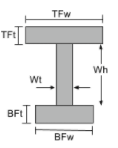	[math] \frac{TFw\times TFt^{3}}{12} +\frac{Wt\times Wh^{3}}{12} + \frac{BFw\times BFt^{3}}{12} +[math] [math] TFw\times TFt\times \left ( BFt + Wh +\frac{TFt}{2} -\bar{y}_{bot} \right )^{2} +[math] [math] Wt\times Wh\times \left ( BFt +\frac{Wh}{2} -\bar{y}_{bot} \right )^{2} +[math] [math] BFw\times BFt\times \left ( \frac{Wh}{2} -\bar{y}_{bot} \right )^{2} [math]	[math] \frac{TFt\times TFw^{3}}{12} + \frac{Wh\times Wt^{3}}{12} + \frac{BFt\times BFw^{3}}{12} [math]
Moment of Inertia Equation of a T-Section
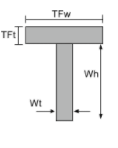	[math] \frac{TFw\times TFt ^{3}}{12} + \frac{Wt\times Wh ^{3}}{12} +[math] [math] TFw\times TFt\left ( Wh + \frac{TFt}{2} -\bar{y}_{bot} \right )^{2} +[math] [math] Wt\times Wh \times \left ( \frac{Wh}{2} – \bar{y}_{bot} \right )^{2} [math]	[math] \frac{TFt\times TFw ^{3}}{12} + \frac{Wh\times Wt ^{3}}{12} [math]
Moment of Inertia Equation of a Channel Section
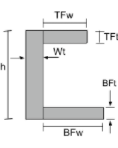	[math] \frac{TFw\times TFt^{3}}{12} + \frac{BFw\times BFt^{3}}{12} + \frac{Wt \times h^{3}}{12} +[math] [math] TFw \times TFt \times \left ( h – \frac{TFt}{2} – \bar{y}_{bot} \right )^{2} +[math] [math] BFw \times BFt \times \left ( \frac{BFt}{2} – \bar{y}_{bot} \right )^{2} +[math] [math] Wt \times h \times \left ( \frac{h}{2} – \bar{y}_{bot} \right )^{2} [math]	[math] \frac{TFt\times TFw^{3}}{12} + \frac{BFt\times BFw^{3}}{12} + \frac{h \times Wt^{3}}{12} +[math] [math] TFt \times TFw \times \left ( Wt + \frac{TFw}{2} – \bar{x}_{left} \right )^{2} +[math] [math] BFt \times BFw \times \left ( Wt + \frac{BFw}{2} – \bar{x}_{left} \right )^{2} +[math] [math] h \times Wt \times \left ( \frac{Wt}{2} – \bar{x}_{left} \right )^{2} [math]
Moment of Inertia Equation of Angles
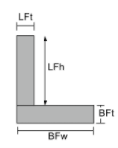	[math] \frac{BFw\times BFt^{3}}{12} + \frac{ LFt \times LFh^{3}}{12} +[math] [math] BFw\times BFt\times \left ( \frac{BFt}{2}-\bar{y}_{bot} \right )^{2} +[math] [math] LFt \times LFh\times \left ( BFt + \frac{LFh}{2}-\bar{y}_{bot} \right )^{2} [math]	[math] \frac{BFt\times BFw^{3}}{12} + \frac{ LFh \times LFt^{3}}{12} +[math] [math] BFt\times BFw\times \left ( \frac{BFw}{2}-\bar{x}_{left} \right )^{2} +[math] [math] LFh \times LFt\times \left ( \frac{LFt}{2}-\bar{x}_{left} \right )^{2} [math]

Use SkyCiv Section Builder for Hand Calculations

In this article, we have walked you through the moment of inertia formula. Did you know SkyCiv Section Builder also shows the full-hand calculations for the following shapes?

• Rectangular, Hollow Rectangular
• Circular, Hollow Circular
• I-Beam, T-Beam
• Angle (L-Beam), Channel
• Triangular sections

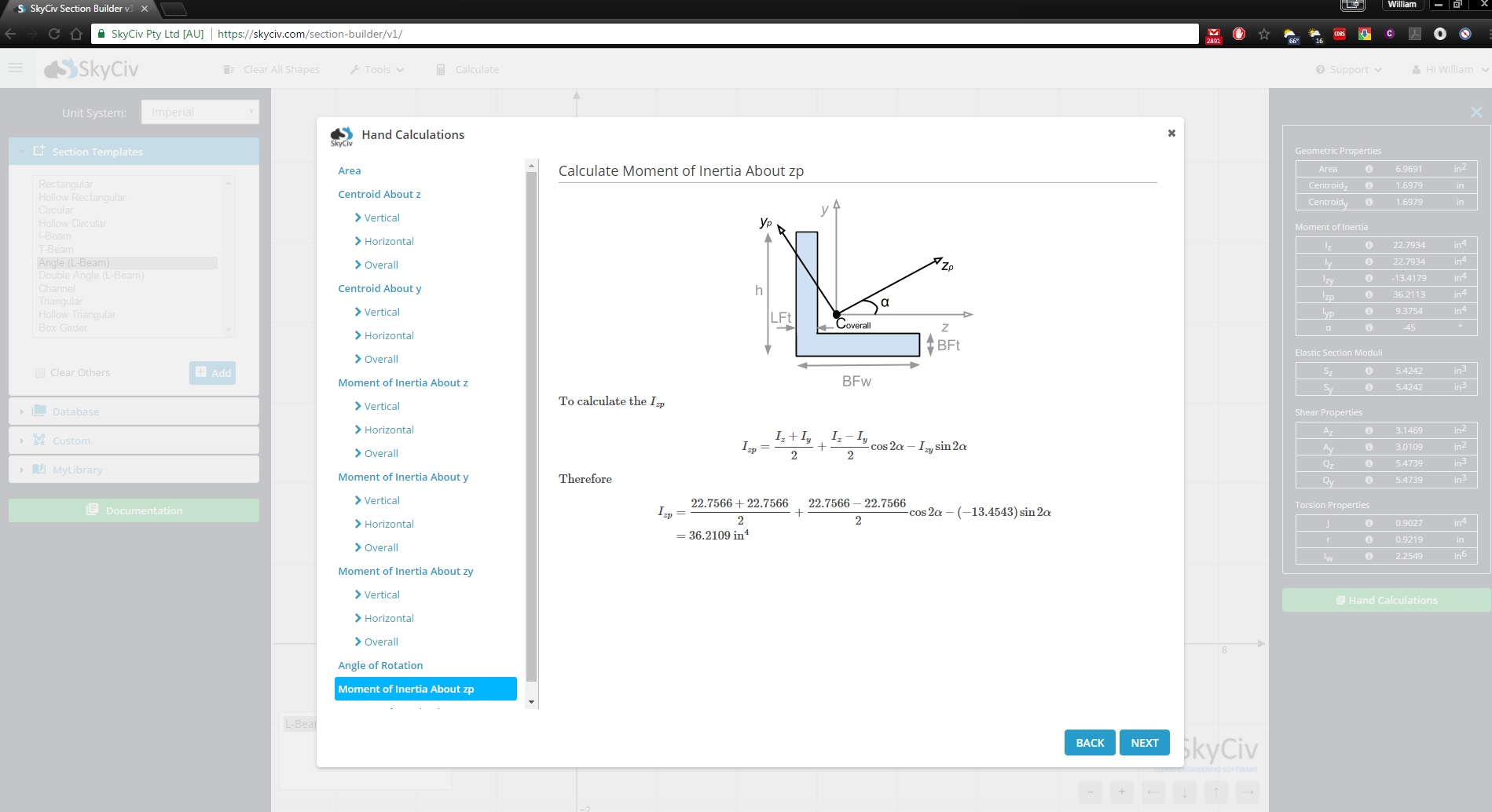
We hope you find the above table valuable for how to calculate a moment of inertia of a circle, triangle, and rectangle moment of inertia among other shapes. We also have a useful Moment of Inertia Calculator, a simplified of SkyCiv Section Builder, that handles these calculations for you or sign up today to get started with SkyCiv software!