- Beam Deflection Definition
- Beam Deflection Unit
- Beam Deflection Equations/Formulas
- Simply Supported Beam Deflection Calculation Example
1. Beam Deflection Definition
What is deflection? Deflection, in structural engineering terms, refers to the movement of a beam or node from its original position due to the forces and loads being applied to the member. It is also known as displacement and can occur from externally applied loads or from the weight of the structure itself, and the force of gravity to which this applies.
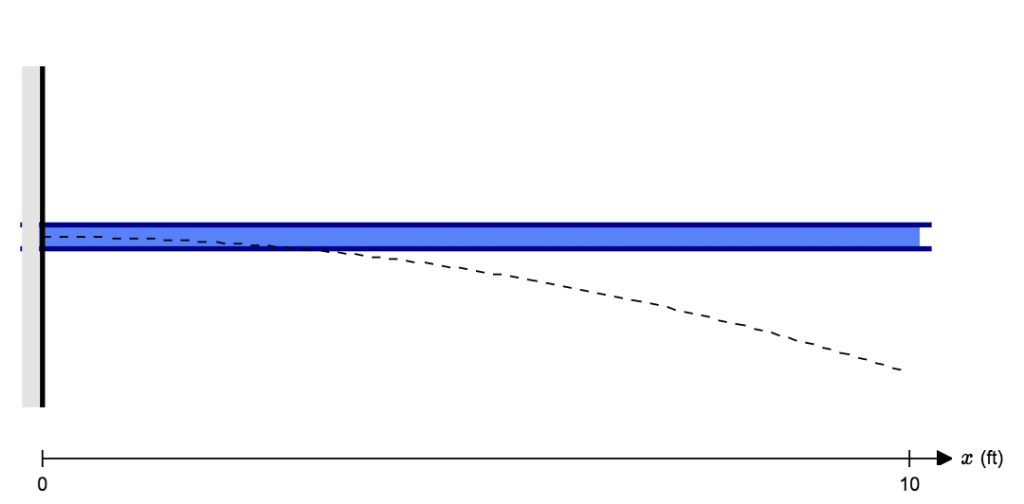
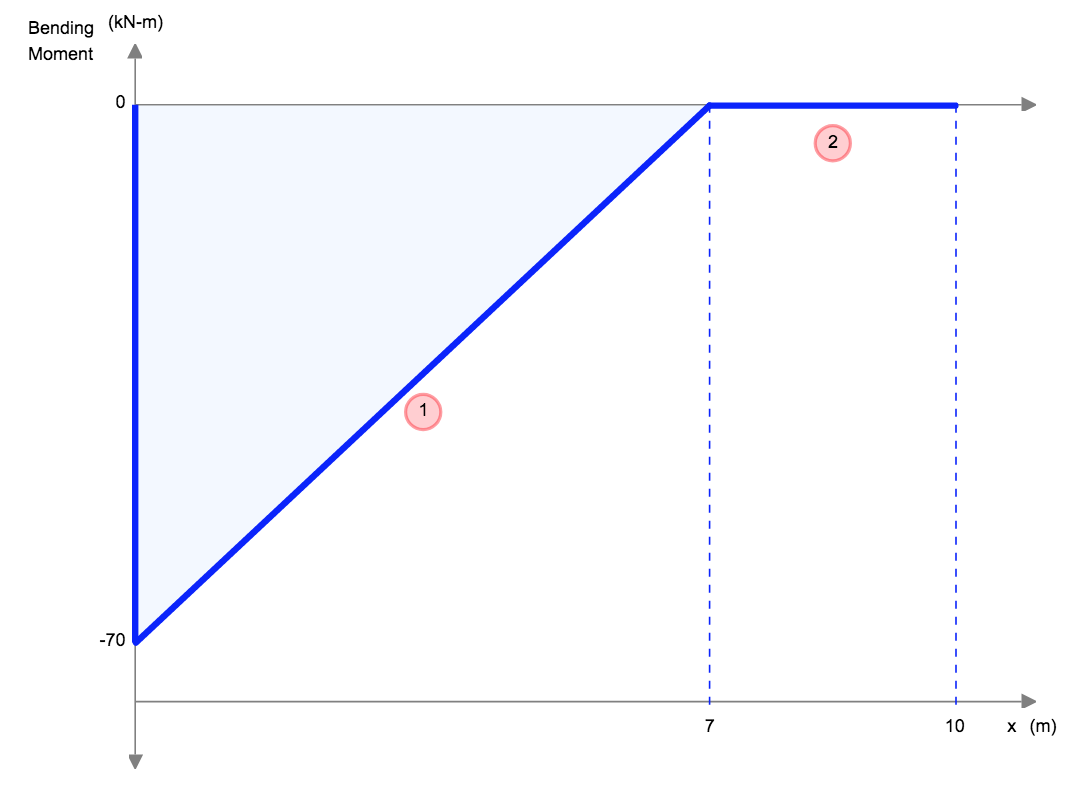
Deflection can occur in beams, trusses, frames, and basically any other structure. To define deflection, let’s take a simple cantilevered beam deflection that has a person with weight (W) standing at the end:

The force of this person standing at the end will cause the beam to bend and deflect from its natural position. In below diagram, the blue beam is the original position, and the dotted line simulates the cantilever beam deflection:
 Source: Beam Deflection Calculator
Source: Beam Deflection Calculator
As you can see, the beam has bent or moved away from the original position. This distance at each point along the member is the meaning or definition of deflection.
There are generally 4 main variables that determine how much beam deflections. These include:
- How much loading is on the structure
- The length of the unsupported member
- The material, specifically the Young’s Modulus
- The Cross Section Size, specifically the Moment of Inertia (I)
2. Beam Deflection Unit
The unit of deflection, or displacement, is a length unit and is normally taken as mm (for metric) and in (for imperial). This number defines the distance in which the beam has deflected from the original position. Since deflection is a short distance measurement (beams should generally only deflect by small amounts), it is commonly expressed in units of length, such as inches or millimeters.
In addition to this, there are other parameters used to measure deflection such as angles, but these units such as radians or degrees are not commonly used. Additionally, it is important to note that the allowable deflection for a structure is often specified as a percentage of the span length (L/X), this is a measure that allows comparison between different beams regardless of their length and its unitless.
3. Beam Deflection Equations/Formulas
The equations are easy to apply and allow engineers to make simple and quick calculations for deflection. If you’re unsure about what deflection actually is, click here for a deflection definition Below is a concise table that shows how to calculate the maximum deflection in a beam. Don’t want to hand calculate these? SkyCiv offers a free beam deflection calculator to help with your needs! For more powerful structural analysis software, sign up for a free SkyCiv Account and get instant access to all the free versions of our cloud structural analysis software!
Use the below formula to calculate the max displacement in beams. Click the ‘check answer’ button to open up our free beam calculator. These beam displacement equations are perfect for quick hand calculations and quick designs.
The deflection of a beam is calculated based on a variety of factors, including materials, the moment of inertia of a section, the force applied, and the distance from support. These can be simplified into simple deflection formula for quick back of the envelope calculations. Here is a simple table of the different loading scenarios and their corresponding max beam deflection formulas:
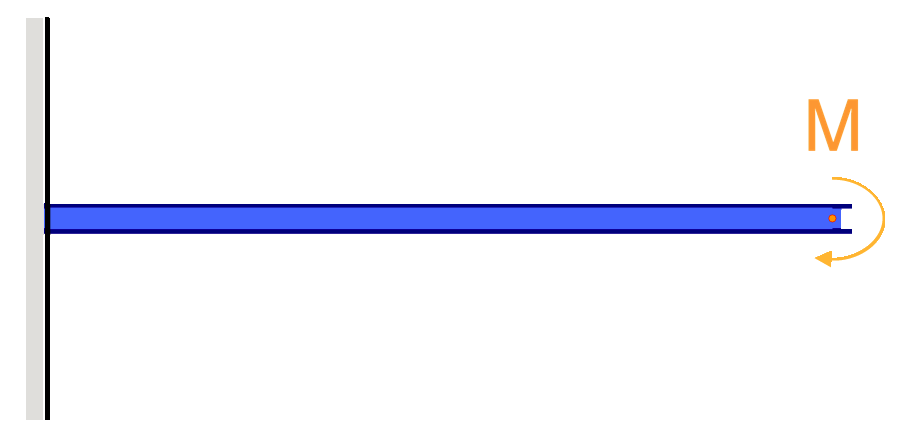
Cantilever Beam Deflection Equations/Formulas
Cantilever beams are special types of beams that are constrained by only one support, as seen in the above example. These members would naturally deflect more as they are only supported at one end.
It is important to consider that the deflection of a cantilever beam is also affected by the position of the load and the location of the fixed support. The farther the load is from the fixed support, the greater the deflection will be. And also, the longer the cantilever the greater the deflection will be, due to the fact that the load is applied to a longer distance.
It’s also important to note that there is a maximum allowable deflection for structures, this value is usually established by building codes and standards, it varies with the type of structure and the purpose of the structure, and the deflection calculated should be within this limit to ensure safety and functionality of the structure.
| Reference | Max Deflection | BMD Shape |
 |
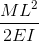 |
 |
 |
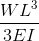 |
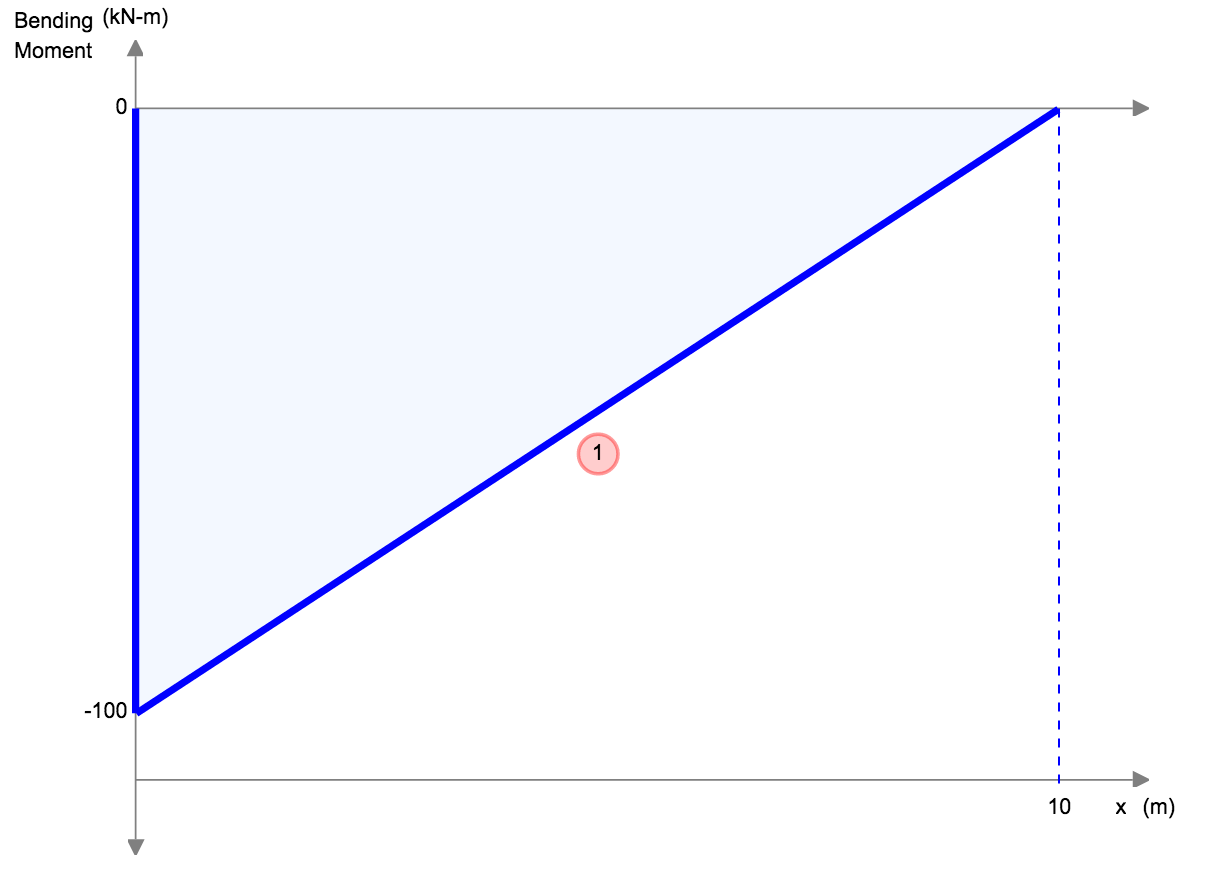 |
 |
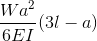 |
 |
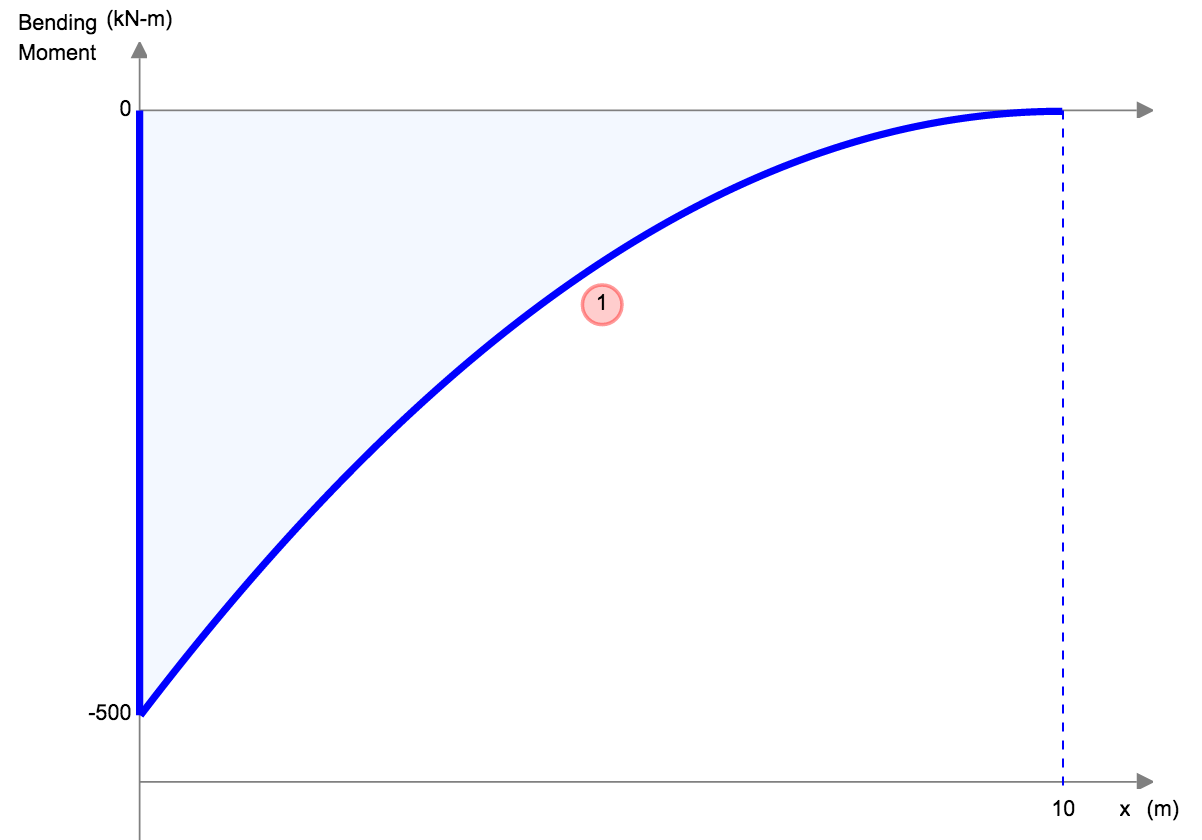
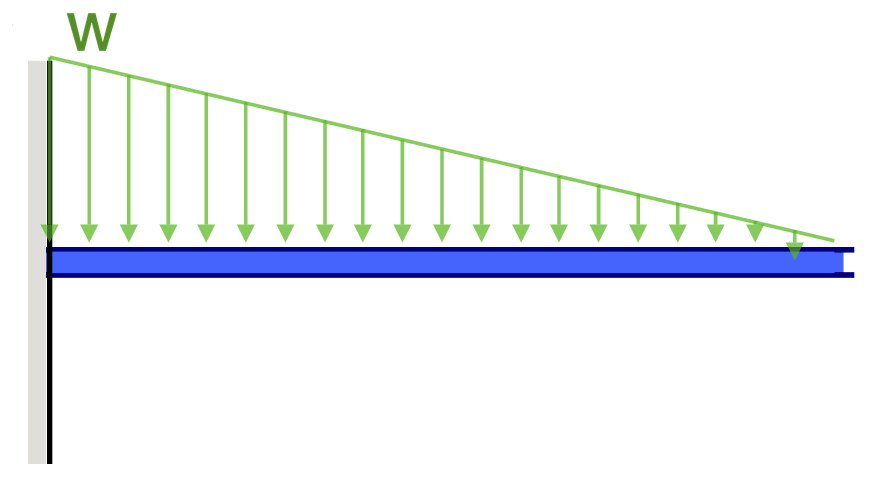
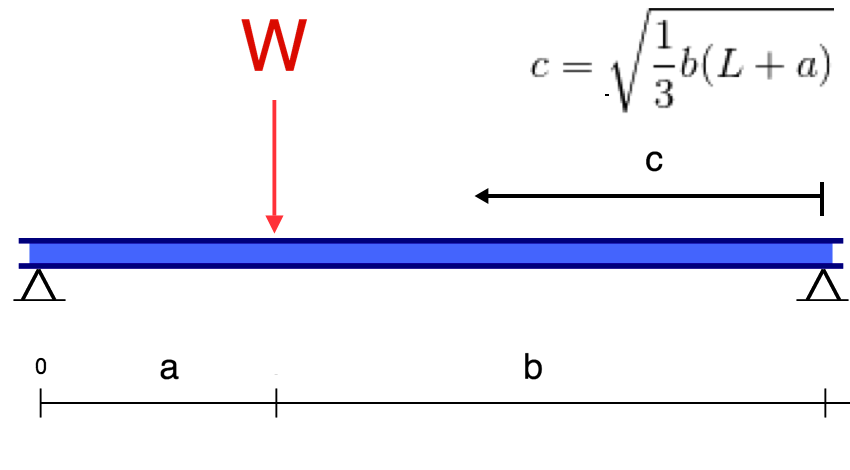
Simply Supported Beam Deflection Equations/Formulas
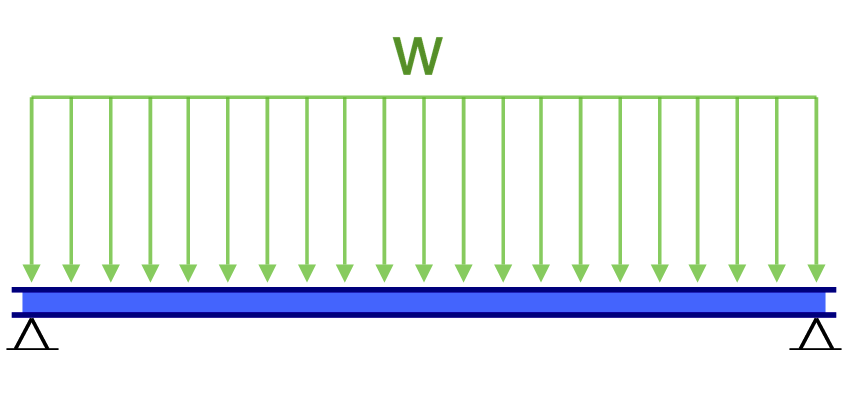
Another example of deflection is the deflection of a simply supported beam. These beams are supported at both ends, so the deflection of a beam is generally left and follows a much different shape from that of the cantilever. Under a uniform distributed load (for instance the self-weight), the beam will deflect smoothly and toward the midpoint.
| Reference | Max Deflection | BMD Shape |
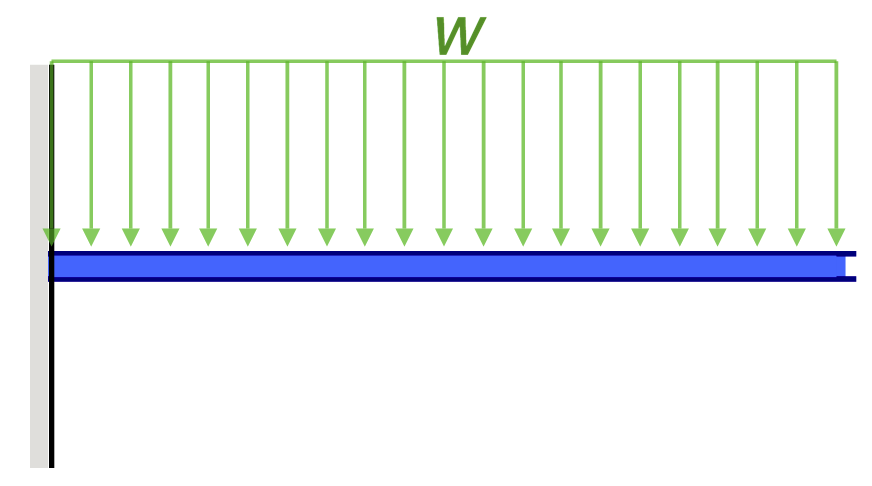 |
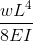 |
 |
 |
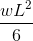 |
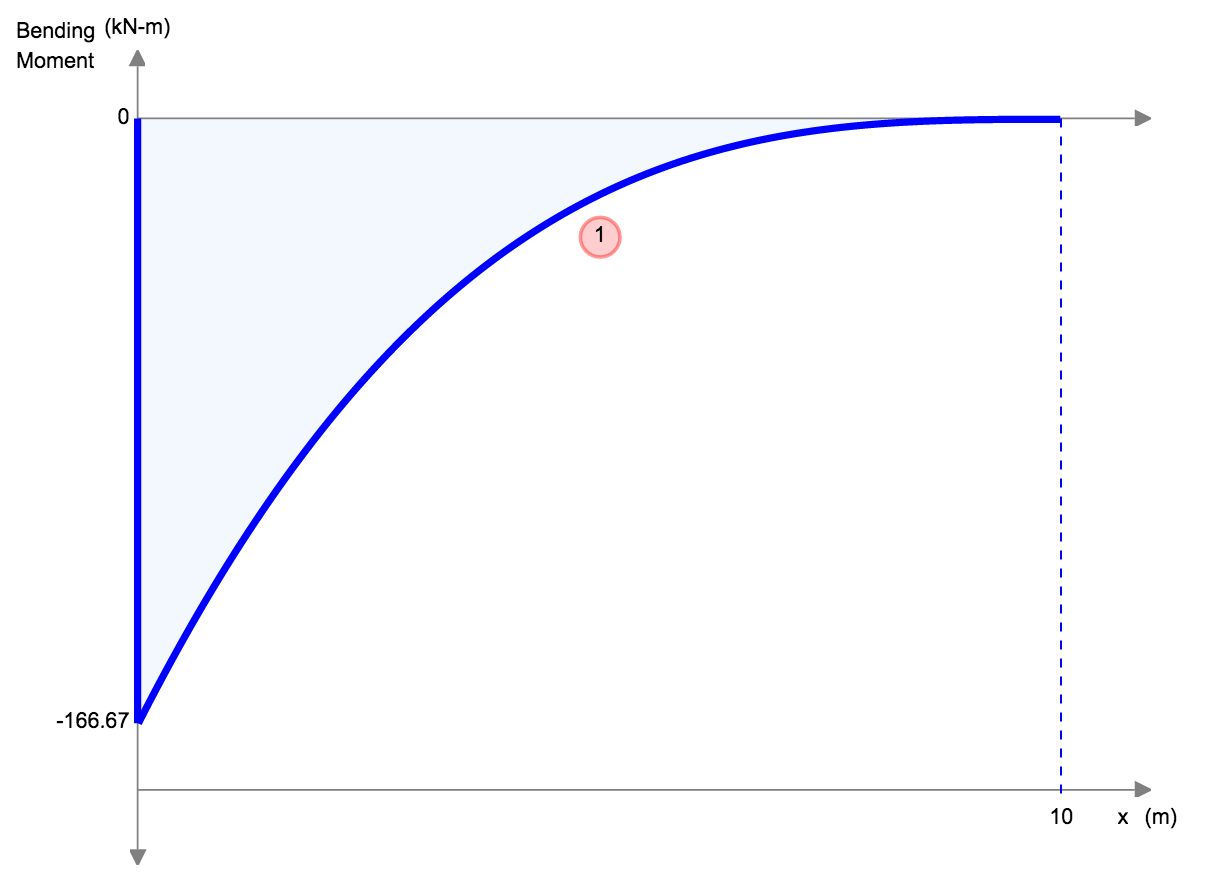 |
 |
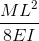 |
 |
 |
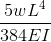 |
 |
 |
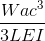 |
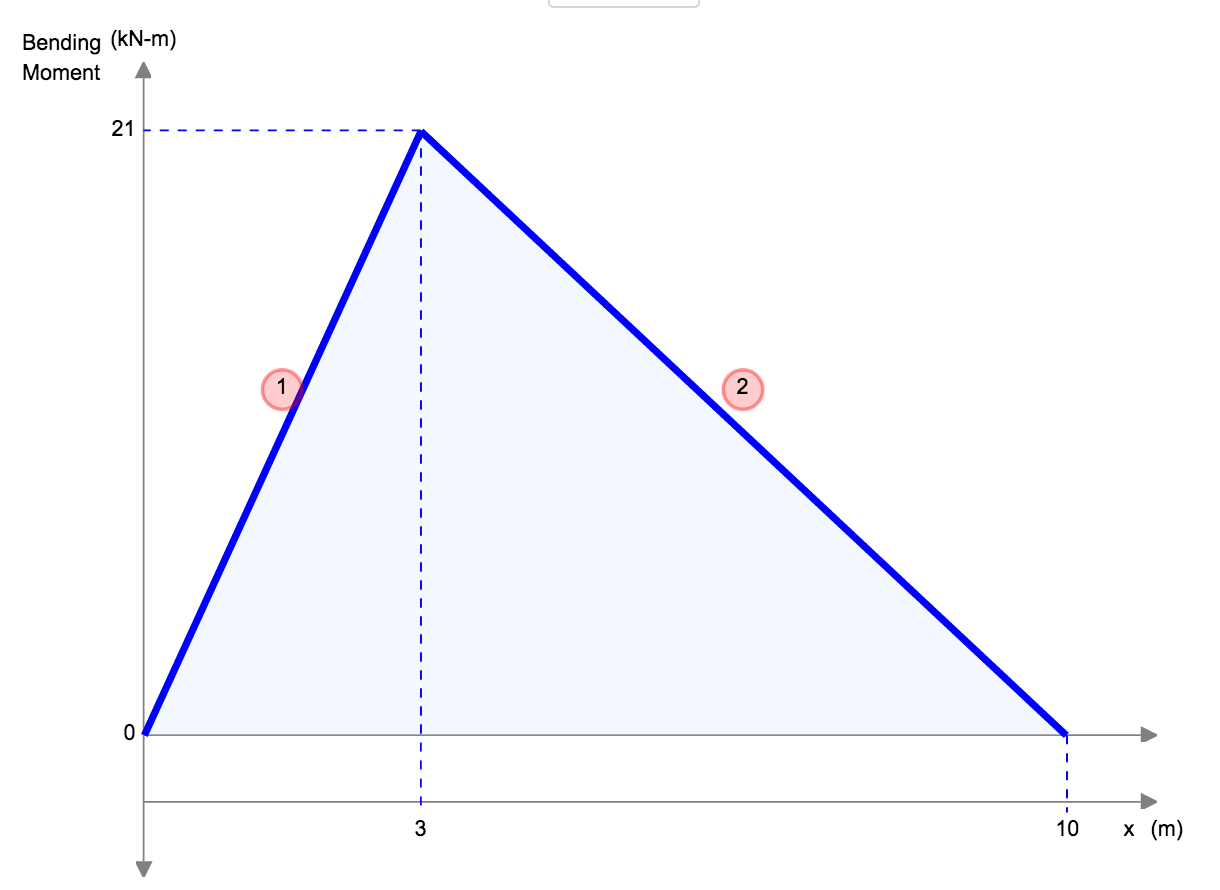 |
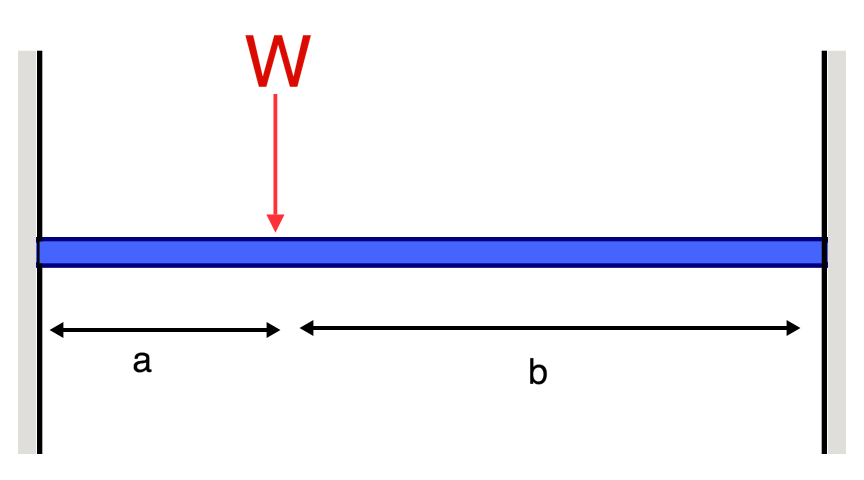
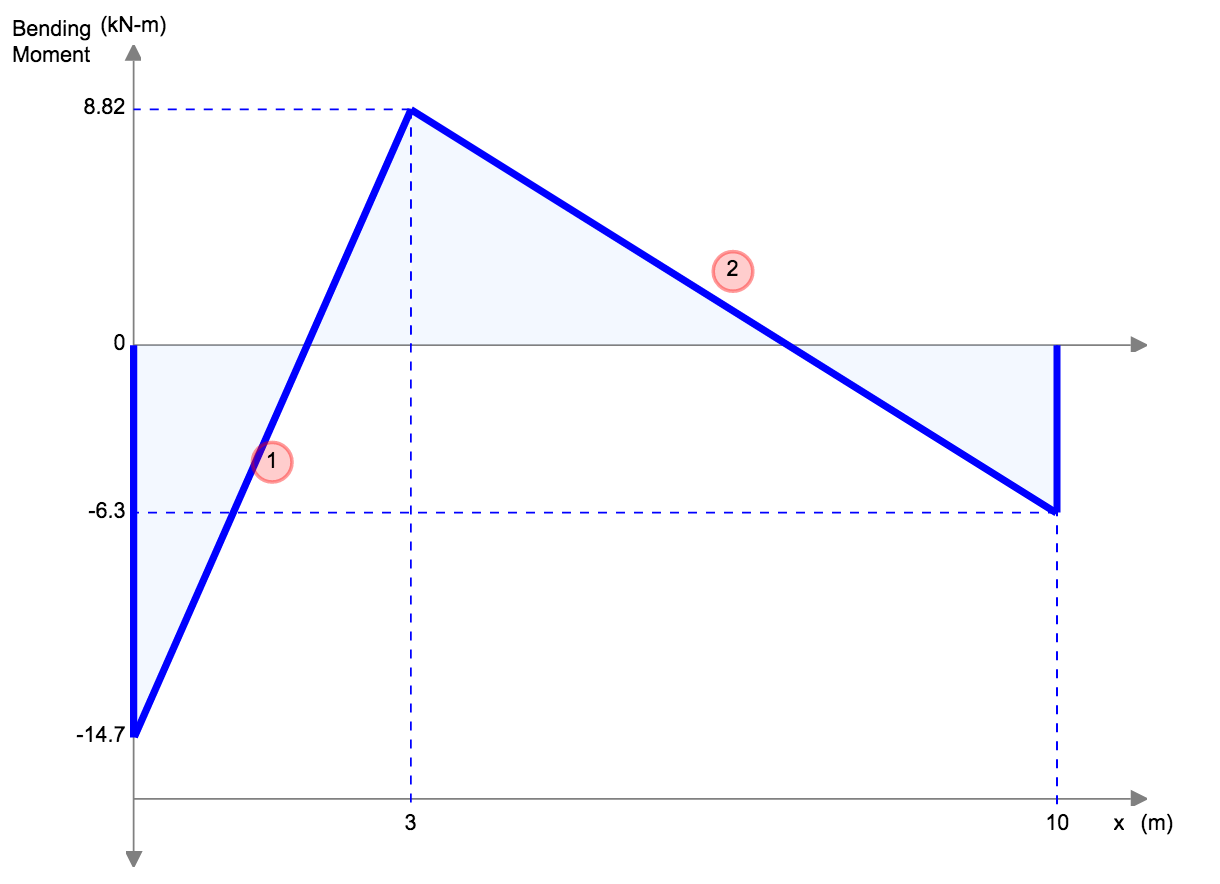
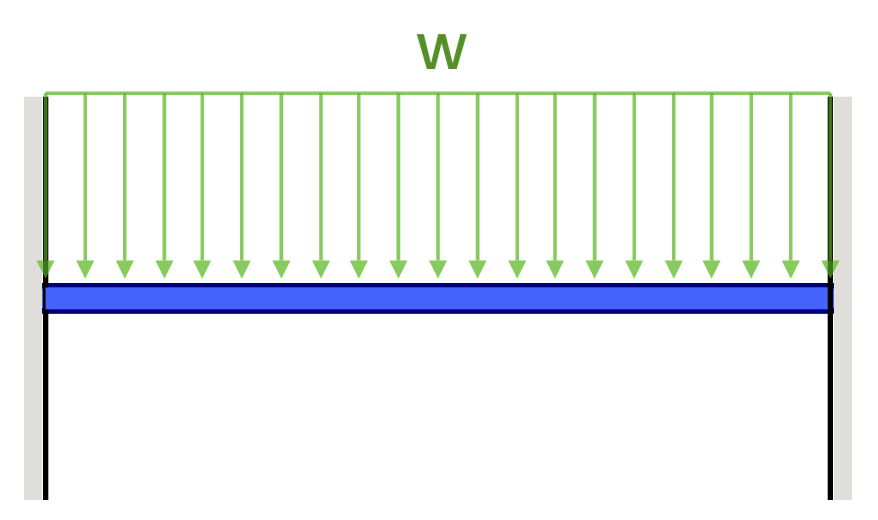
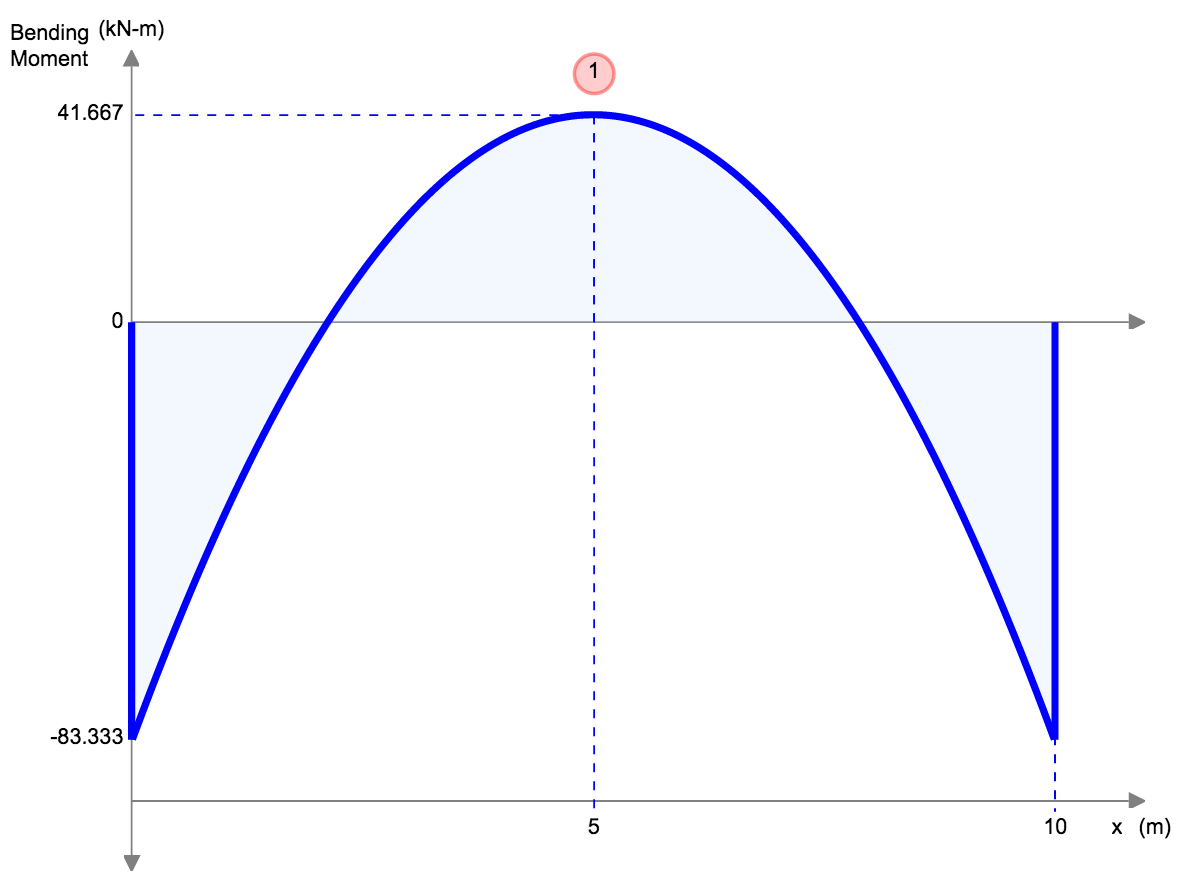
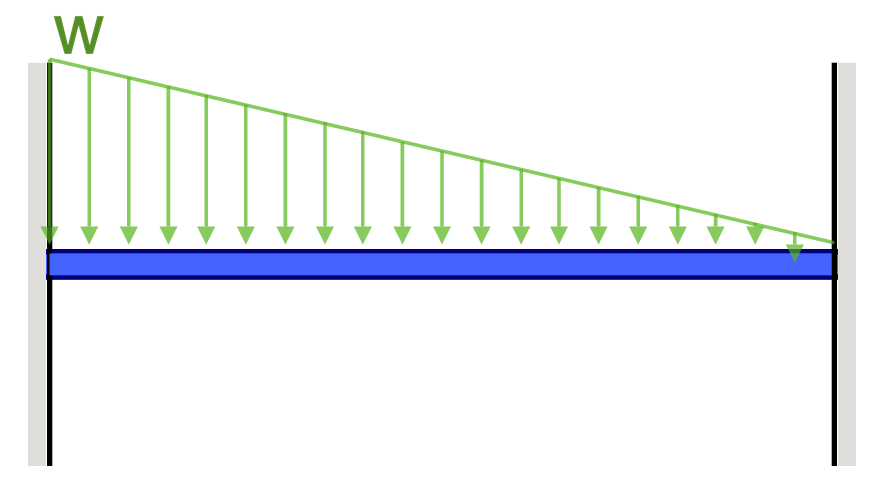
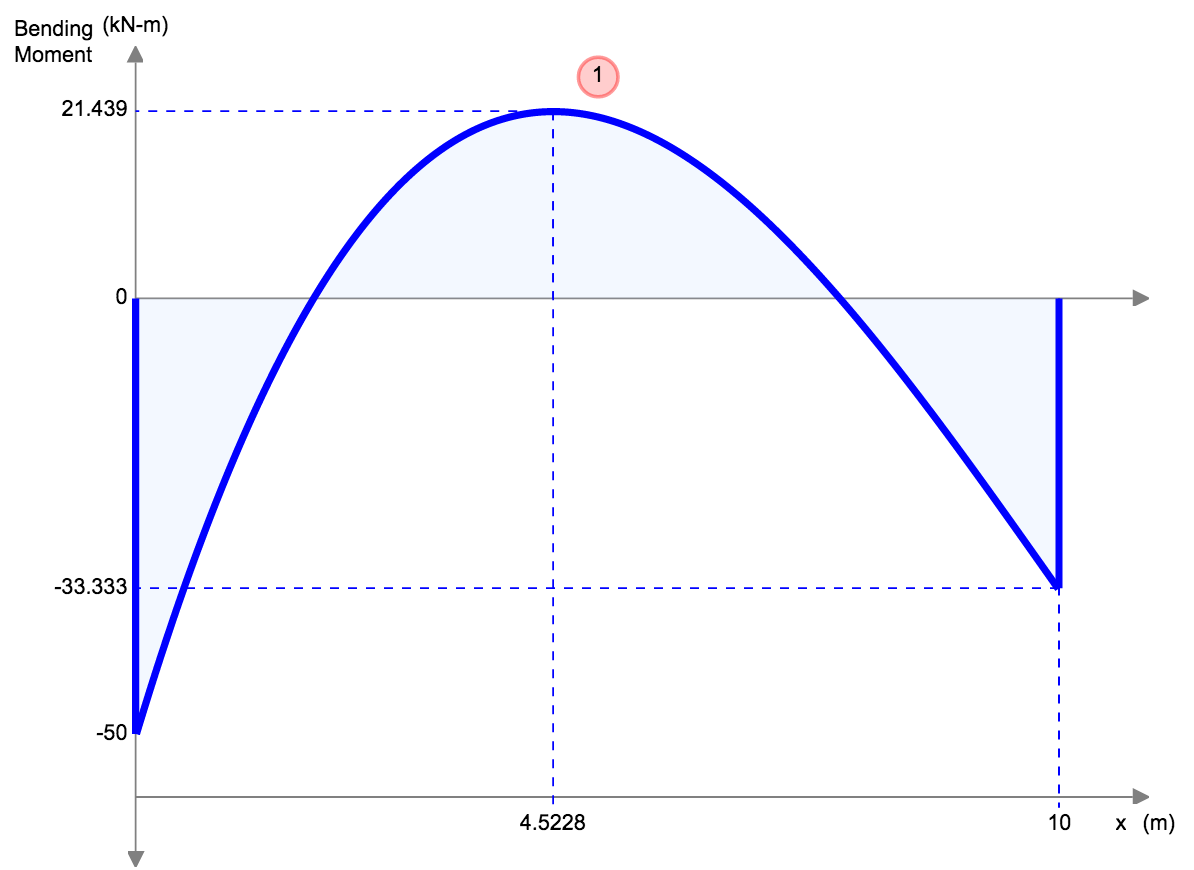
Fixed Beam Deflection Equations/Formulas
| Reference | Max Deflection | BMD Shape |
 |
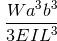 |
 |
 |
 |
 |
 |
 |
 |
4. Simply Supported Beam Calculation Example
Let’s consider a simple supported beam with a span of L = 10 m, a uniform load of w = 10,000 N/m, and the following material properties: Young’s modulus, E = 200 GPa, the moment of inertia, I = 0.0015 m^4.
The deflection of the beam can be calculated using the equation, taken from our above table of equations:
\(δ = (5wl^4)/(384EI) \)
\(δ = (5 * 10,000 * 10^4)/(384 * 200 *10^9 * 0.0015) \)
\(δ = 0.00434 m = 4.34mm \)
So the deflection of the beam is 0.00434 m or 4.34 mm. It’s always important as an engineer to verify your result, so let’s plug the same numbers into SkyCiv’s Free Beam Calculator:
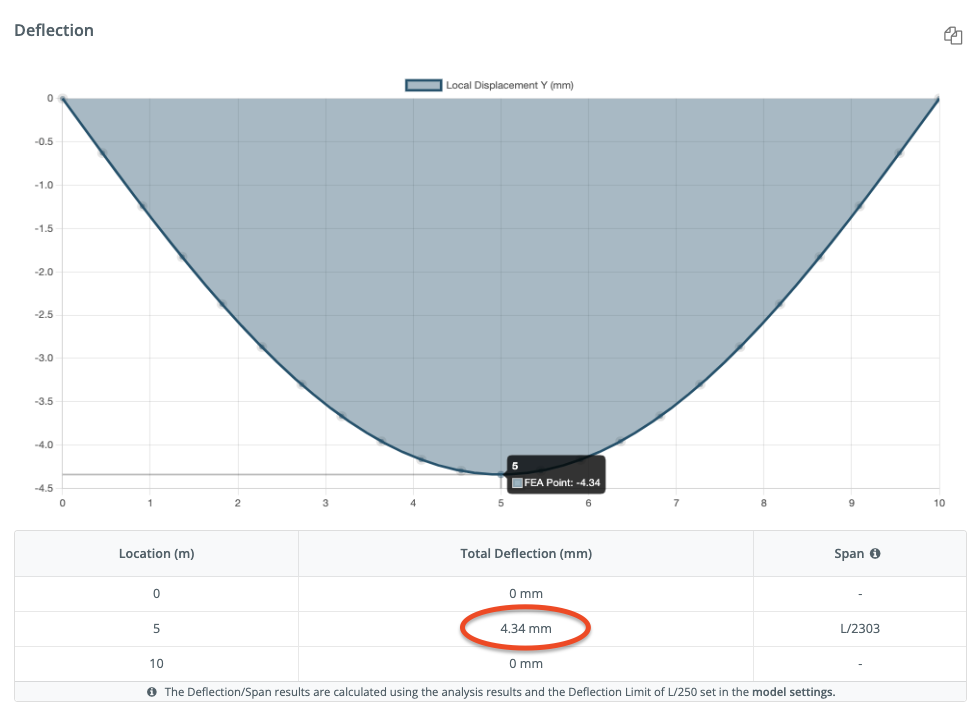
It’s worth mentioning that this is a very simple example and in practice, there are various other factors that need to be considered like the effects of temperature change, live load, self-weight and many other things, in a real life scenario, a structural engineer would take these factors into account while calculating the deflection of a beam.
SkyCiv Beam Software
SkyCiv Beam Analysis Software allows users to analyze beam structures easily and accurately. You can get an analysis of your beam member, including reactions, shear force, bending moment, deflection, and stresses in a matter of seconds.
If you want to give it a try first, our FREE Beam Deflection Calculator is a great way to start, or simply sign up for free today!


