Free Online Beam Calculator
Calculate reactions, shear force, bending moment, deflection and stress for cantilever or simply supported beams
About the SkyCiv Beam Calculator
Table of contents:
How to use SkyCiv Beam Calculator
Welcome to Beam Calculator, our free version of the SkyCiv Beam Analysis Software! Our calculator generates the reactions, shear force diagrams (SFD), bending moment diagrams (BMD), deflection, and stress of a cantilever beam or simply supported beam. SkyCiv Beam tool guides users along a professional beam calculation workflow, culminating in the ability to view and determine if they comply with your region's Design Codes.
Watch the video tutorial below to get started with our calculator.
Written instructions
To use the calculator, simply follow these steps:
- Input your beam length using the 'Beam' menu.
- Use the 'Supports' menu to apply your support type at any location along your beam. Available support types include:
- Pin Support
- Roller Support
- Fixed Support
- Spring Support
- Use the 'Section' menu to apply a custom Moment of Inertia (Iz) or Young's Modulus (E) value. Alternatively, we also include a button to use SkyCiv's Section Builder Tool:
- This opens a new menu with our fully integrated Section Builder, allowing you to access preset Database Shapes we've included from all around the world. Section Builder also allows you to easily create and save custom shapes using the Shape Templates option. Learn more about SkyCiv Section Builder.
- After selecting your section, you have the opportunity to add any hinges along the beam span under the 'Hinge' menu.
- Your beam is now set up! Now we can apply the loads that you'd like to assess the beam's resistance to. Use the 'Point Loads', 'Moments', or 'Distributed Loads' menus to apply one or multiple of those load kinds onto your created beam. We also highly recommend specifying the different load cases each load corresponds. You can do so using the 'Load Case' drop down menu before adding each respective load.
- The reason for adding Load Cases becomes apparent now in the final step. Open the 'Load Combinations' menu to apply different factors for each Load Case.
- Alternatively, use our 'Import from Design Code' function to automatically assign the loads you created to the specific load combinations prescribed by your region's Design Code!
- One final load to consider is Self Weight. Use the 'Self Weight' toggle button on the top right of the calculator to turn on or off a consideration of self weight. We automatically calculate self weight based on your chosen beam length, material, and section shape.
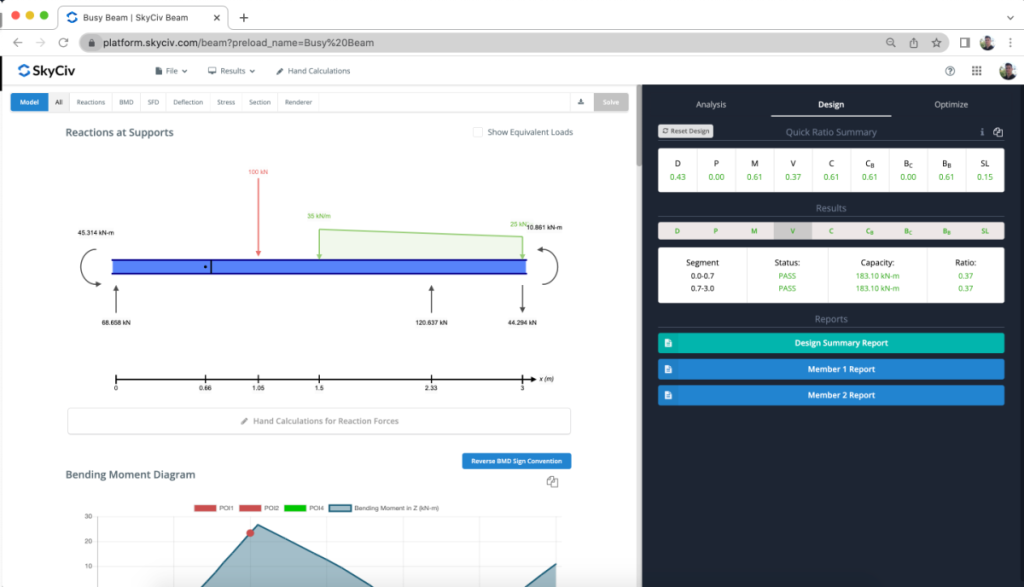
- Now that our beam and loads have been assigned, let's solve! Click the green 'Solve' button on the top right of the calculator. You'll be greeted with a super easy to use results page that includes the following functionality:
- View:
- Reactions
- Bending Moment Diagram
- Shear Force Diagram
- Deflection and Span calculation
- Stress Calculation
- Section Properties
- 3D Render
- Download a customised selection of the above results in a formatted PDF report.
- Use the 'Analysis' tab to view various criteria, such as:
- Deflection
- Custom Stress Limit
- Material Yield
- Material Strength
- Use the 'Design' tab to instantly check the beam against your region's specific code requirements! This is insanely useful!
- Use the 'Optimize' tab to change your chosen section size based on criteria you can choose. This is so handy if you picked a section size too big or too small and would like us to help you decide.
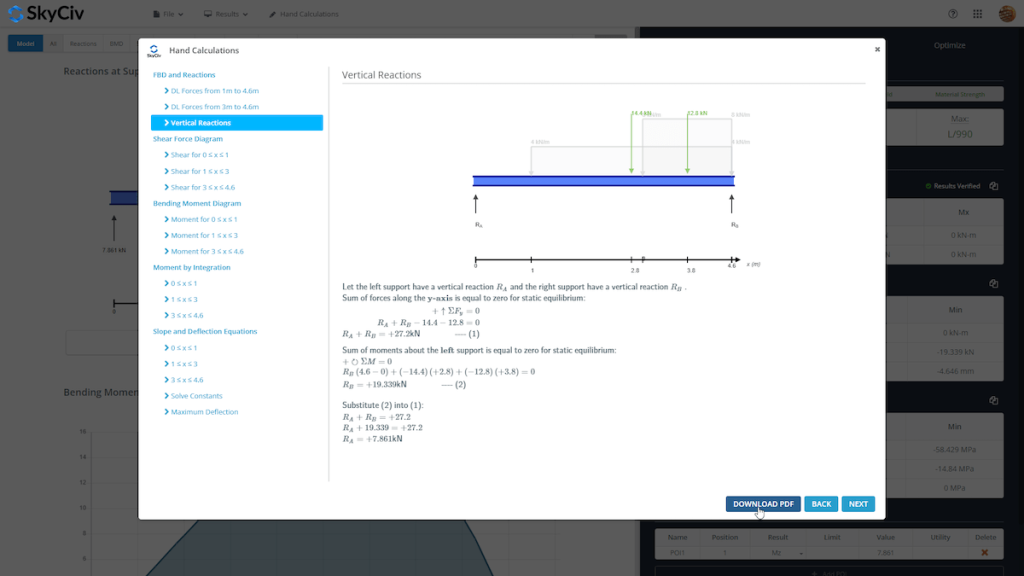
- There's even more functionality in the results page, including CSV exporting and Hand Calculations.
Beam Deflection Calculator
One of the most powerful functions is using it as a beam deflection calculator (or beam displacement calculator). This can be used to observe the calculated deflection of a simply supported beam or of a cantilever beam. Being able to add section shapes and materials, this makes it useful as a wood or steel beam calculator for lvl beam or i beam design. For now, this functionality is available in SkyCiv Beam which has a lot more functionality for timber, concrete and steel beam design.
What is beam deflection?
Beam deflection is when a beam bends or sags under its own weight or due to applied loads. Basically, it's the amount of displacement or bending that a beam experiences when subjected to a load. Think of it like a diving board. When you stand on the end of the diving board, it bends and dips down. That's beam deflection in action! The diving board is the beam and your weight is the load that's causing it to bend.
In engineering, it's important to understand and calculate beam deflection because it can affect the overall strength and stability of a structure. Too much deflection can result in failure, so engineers need to design beams that are strong enough to resist deflection under the loads they will experience. Beam deflection is one of the serviceability criteria that engineers consider when designing structures. This is because excessive deflection can result in unwanted aesthetic effects, such as sagging floors, cracking of finishes, or discomfort for the users. Therefore, engineers aim to limit deflection to acceptable levels so that the structure performs satisfactorily and provides a comfortable environment for the users.
How to calculate beam deflection
Calculating beam deflection can seem intimidating at first, but it's actually not too complicated when you break it down. Engineers can also use empirical formula to quickly calculate the deflection of a beam which is what we'll use for the below example:
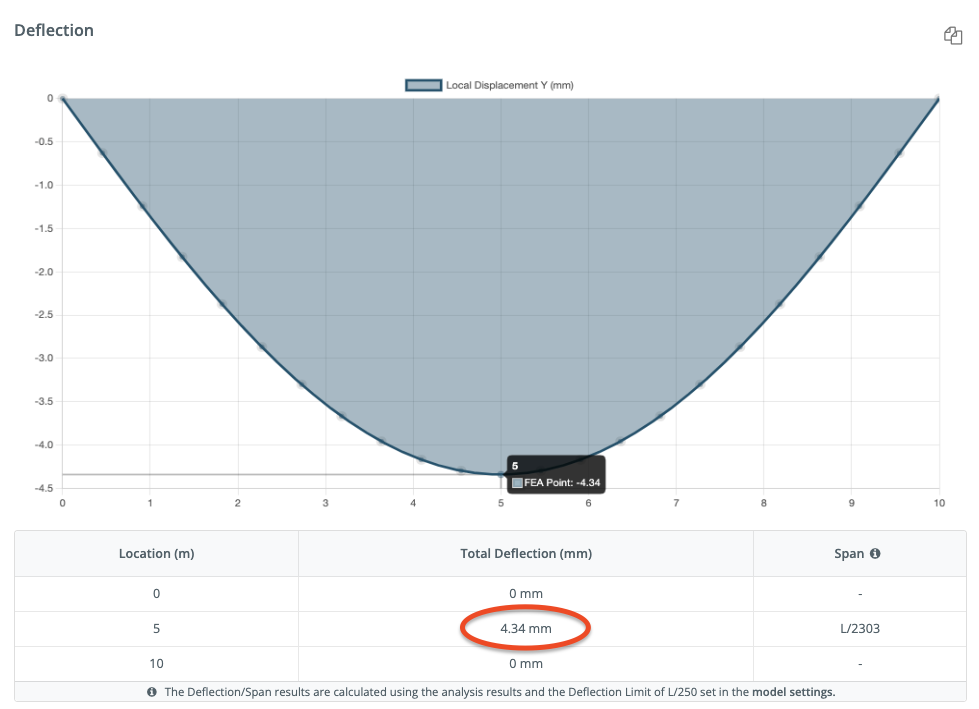
Let’s consider a simple supported beam with a span of a uniform load of w = 10 kN/m over a L = 10m span, and the following material properties: Young’s modulus, E = 200,000 MPa, and the moment of inertia about the y axis is I = 0.0015 m^4. The deflection of the beam can be calculated using the equation, taken from SkyCiv's Beam Deflection Formula page.
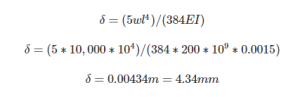
It’s always important as an engineer to verify your result, so let’s plug the same numbers into SkyCiv’s Free Beam Deflection Calculator:
What materials can this beam load calculator calculate?
The quick answer is anything! The above tool can be used as a steel beam calculator, a timber calculator or even used for concrete structures. The input for material can be changed to suite whatever material you wish to design. For instance, the user would enter in a Young's Modulus of about 200,000 MPa (or 29,000 ksi for imperial units). For simplicity, the free tool only takes the materials Young's Modulus, however our full version will also take in Yield/Ultimate Strength, Density and Poisson's Ratio.
Beam Reaction Calculator
SkyCiv's above reaction forces beam calculator is capable of quickly and easily calculating the support reaction forces of your cantilever or simply supported beams. Add a number of forces and different support conditions and locations to get the reactions at supports. Want to learn more about reactions, read on for a detailed guide on reaction forces.
What are reaction forces?
Reaction forces are the supporting forces that exist in a response to applied loads. They are the forces that balance the applied loads, ensuring that the structure remains in equilibrium and static, which are critical structural engineering conditions. Reaction forces can be thought of as the "support forces" that counteract the forces exerted by the loads on the structure. They can be determined using the principles of statics and mechanics of materials. In terms of beam reaction forces, these are usually the resultant forces from the pinned, fixed or roller supports. They are usually comprised of the following reaction forces (assuming forces are applied in vertical and horizontal directions:
- Fixed Supports - usually have a Vx, Yy (horizontal, vertical reactions) and Mz (moment reaction)
- Pinned Supports - usually have vertical and horizontal reaction forces only (Vx, Vy)
- Roller Supports - typically will only have a vertical reaction force (Vy)
The beam span calculator will easily calculate the reactions at supports. It is able to calculate the reactions at supports for cantilever or simple beams. This includes calculating the reactions for a cantilever beam, which has a bending moment reaction as well as x,y reaction forces. The reactions at supports are also useful in calculating the entire force in the structure. Simply add these values together, and you can calculate the total amount of force applied to your structure.
How to calculate the reaction forces on a beam?
Reaction forces on a beam can be calculated by solving the following equilibrium equations:
∑Fy = 0
(All the vertical forces and vertical support reactions sum to 0)
∑Mz = 0
(Moment forces sum to 0)
It's often helpful to look at a simple example. Consider a simply supported beam of length L = 10m with a uniform load (force per unit length) of w = 5 kN/m acting on it. The supports are located at points A and B. The reaction forces at the supports are denoted as R_A and R_B.
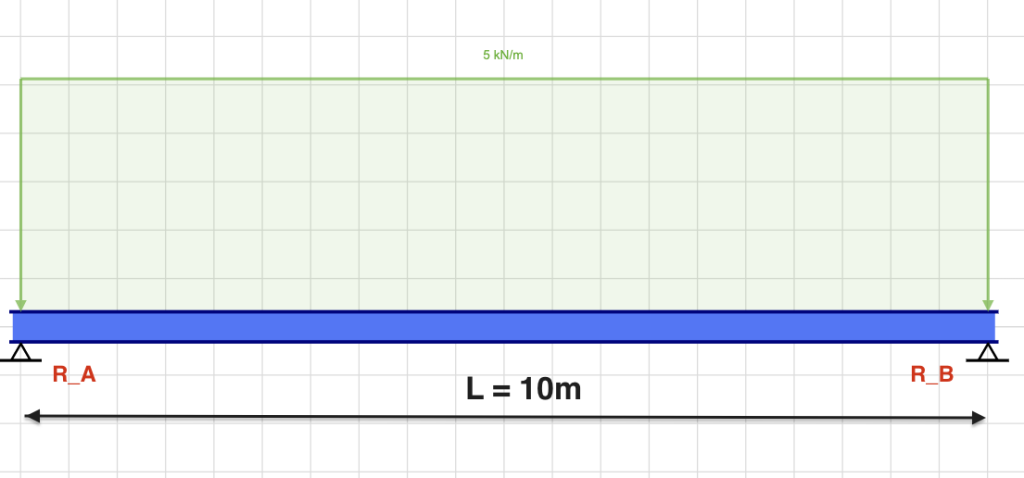
To calculate the reaction forces, we can use the following steps:
- Draw a free-body diagram of the beam, showing all the loads and the supports. (see above)
- Sum up the forces in the vertical direction. In a simply supported beam, the only vertical force is the 5kN/m force, which when multiplied by the length of the member (L = 10) we get 5*10 = 50 kN. Write an equation for the vertical forces:
∑Fy = 0
= RA + RB - wL
= RA + RB - 5*10
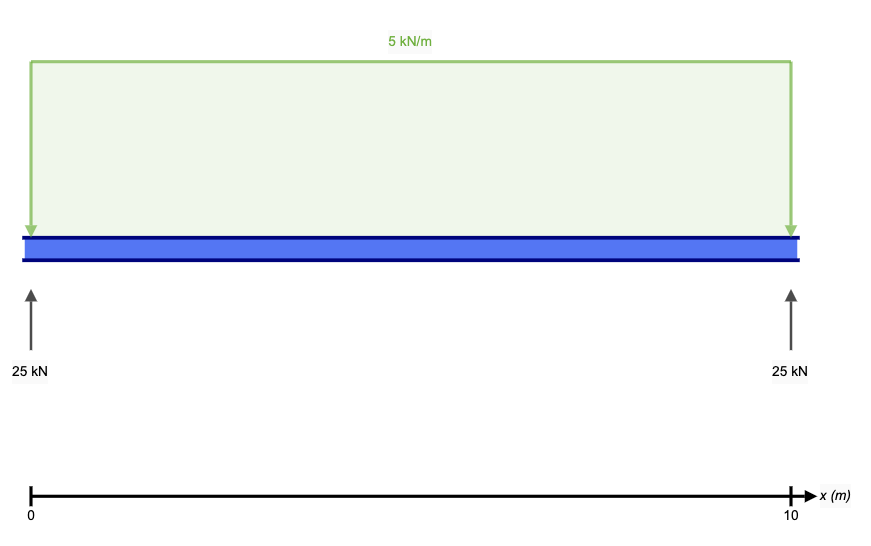
RA + RB = 50 kN
- Use the sum of moments to calculate one of the reactions (usually the left side, in this case R_A):
∑Mz = 0
0 = -50 kN (-5m) + RB(-10m) + RA(0)
RB = 25kN
Therefore, RA = 25kN
Obviously this is just a simple example and more complex structures will require additional calculations to determine the reaction forces - for this we have a more detailed tutorial on how to calculate reaction forces in a beam. Additionally, in real-world scenarios, the beam may also experience other loads and forces such as shear, bending moment, and deflection, which need to be considered in the analysis and design. SkyCiv's above beam load calculator can be used to calculate reaction forces for beams with simple supports or cantilever supports. So we can verify the results using the above calculator:
Bending Moment Calculator
What is a bending moment diagram?
A bending moment diagram is a graphical representation of the bending moment forces along a structural member, such as a beam. The diagram shows the values of the bending moment along the length of the beam.
The bending moment is a measure of the bending force in a beam and is calculated by multiplying the load by the distance from the neutral axis. The neutral axis is an imaginary line which cuts across the centroid of the cross-section - technically where there is no change in the length of the fibers. The bending moment can be positive, negative, or zero depending on the direction and magnitude of the load. The direction of the bending force depends on sign conventions, but by default the SkyCiv software will show a positive bending moment diagram when the beam's top fibers are compressed.
A bending moment diagram is an important tool for engineers because it allows them to understand the behavior of the beam under load and to design the beam to resist the loads safely and efficiently. The diagram can be used to determine the maximum and minimum bending moments and their locations.
How to calculate a bending moment diagram using the above tool
Bending Moment Diagrams can be quickly and easily generated using the above calculator. Within minutes, you'll have neat and clear diagrams, no matter how complex the beam. To calculate a bending moment diagram using the above beam load calculator, simply:
- Enter Beam Length
- Add supports (two supports for simply supported, single Fixed support for cantilever)
- Apply forces (or toggle on Self Weight)
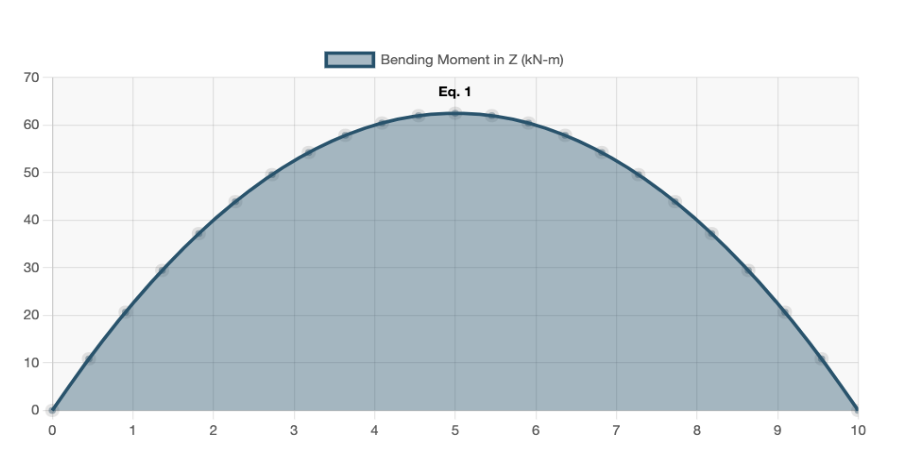
- Run Calculate which will generate the bending moment diagram of the beam:
For more information, visit our documentation on how to find bending moment.
Bending moment formulas
There are a number of bending moment formulas that can be used to quickly and easily calculate the max bending moment forces in a range of different beam setups. There are available on another page on our website called Bending Moment Formula.
Shear Force Calculator
What is a shear force and a shear force diagram?
A shear force diagram is a valuable tool used in structural engineering to represent the distribution of shear force along a beam or any other structural element. It is a graphical representation with the position of the beam plotted along the horizontal axis and the magnitude of shear force plotted along the vertical axis. This diagram helps engineers determine the maximum shear force and its location, which are crucial in determining the design requirements for the element. Understanding and constructing shear force diagrams is an essential part of the structural analysis process.
Here's an example of a shear force caused by a point load at 7.5m, taken from the above shear force calculator:
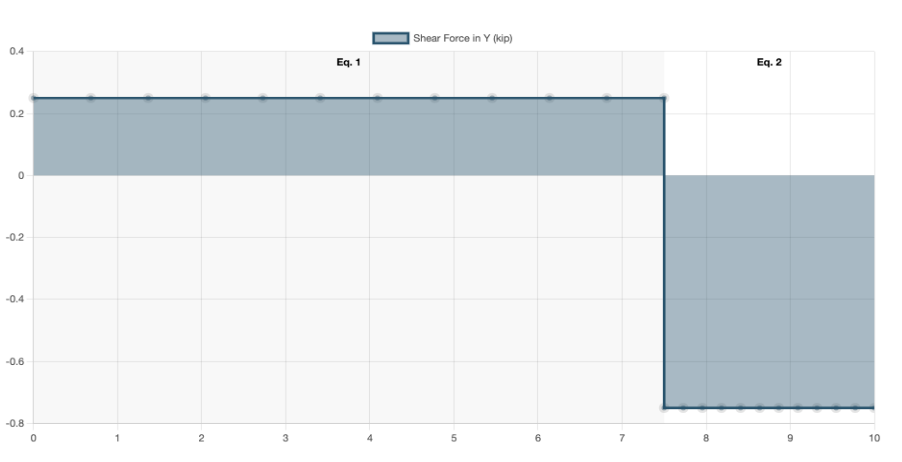
How to calculate the shear force in a beam
SkyCiv has an extensive article on how to calculate the shear force diagram in a beam. In short, you would simple move along the beam plotting the vertical force and how it changes along the member. You will generally need to start by calculating the reaction forces (shown in the above segment) before plotting the shear force diagram. Use the sign convention to determine the direction of the shear force, where positive shear force is assumed to rotate the beam section counterclockwise while negative shear force is assumed to rotate the beam section clockwise. The main formula or equation we use in calculating shear force is the following equilibrium equation:
∑Fy = 0
The full version of the above shear and moment diagram calculator will automatically show you the process step by step, with interactive hand calculation module. Here's an example of a cut made just after the first support (which has an upward force of 0.25 kip):
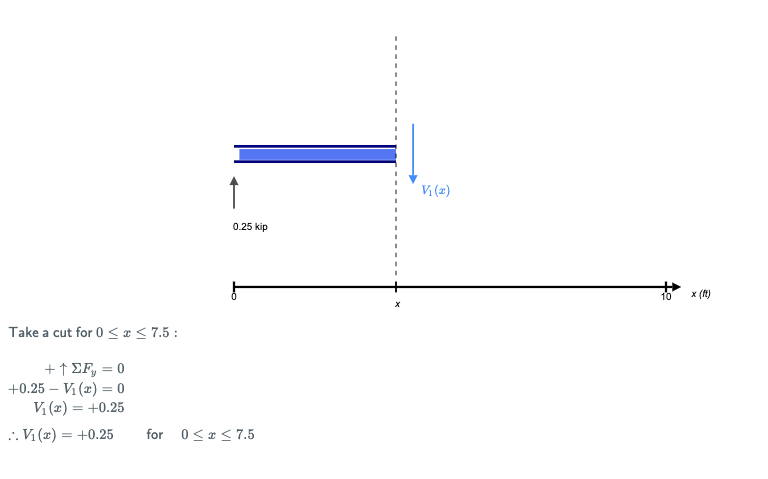
By taking the sum of forces in Y, we can see there would be a positive shear force in the beam. This would remain constant, until the point load which acts at 7.5m along the beam. After that point load, you'll see that by summing the forces, the shear force ends up being negative:
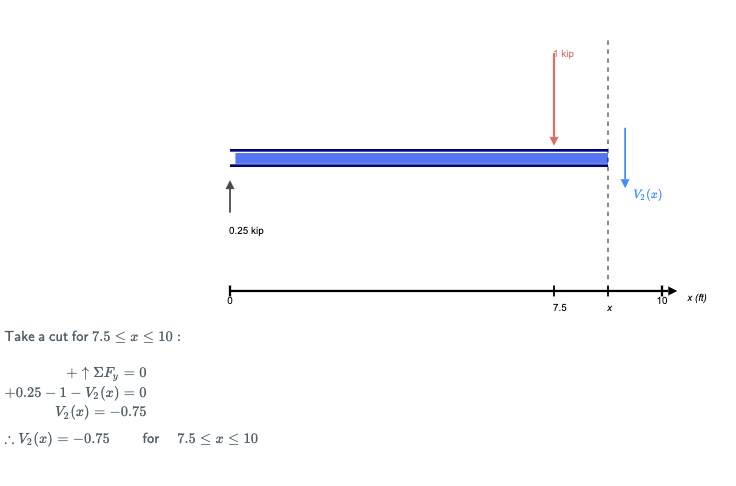
Plotting this, we can get the full shear force diagram:

Bending moment shear force calculator
The above steel beam span calculator is a versatile structural engineering tool used to calculate the bending moment in an aluminium, wood or steel beam. It can also be used as a beam load capacity calculator by using it as a bending stress or shear stress calculator. It is able to accommodate up to 2 different concentrated point loads, 2 distributed loads and 2 moments. The distributed loads can be arranged so that they are uniformly distributed loads (UDL), triangular distributed loads or trapezoidal distributed loads. All loads and moments can be of both upwards or downward direction in magnitude, which should be able to account for most common beam analysis situations. Bending Moment and Shear Force calculations may take up to 10 seconds to appear and please note you will be directed to a new page with the reactions, shear force diagram and bending moment diagram of the beam.
I Beam Calculator
The above calculator is able to analyse a range of beam types - including i beams, channels, hollow rectangular and even custom shapes. So, although many refer to it as a i beam calculator, it is so much more!
Build custom shapes in our section builder, or load from common libraries such as AISC, AISI, Australian steel design, European and Canadian libraries to name a few. Loading a section is instant, and users can even make the most of powerful search functionality to help you find what you're looking for.
About SkyCiv
SkyCiv offers a wide range of Cloud Structural Analysis and Design Software for engineers. As a constantly evolving tech company, we're committed to innovating and challenging existing workflows to save engineers time in their work processes and designs.