Free Moment of Inertia and Centroid Calculator
Calculate Moment of Inertia, Centroid, and Section Modulus for a wide variety of shapes
A Comprehensive Guide to our Moment of Inertia Calculator
SkyCiv Moment of Inertia and Centroid Calculator helps you determine the moment of inertia, centroid, and other important geometric properties for a variety of shapes including rectangles, circles, hollow sections, triangles, I-Beams, T-Beams, angles and channels. We also have some articles below about how to calculate the moment of inertia, as well as more information on centroids and section modulus.
You can solve up to three sections before you're required to sign up for a free account - which also gives you access to more software and results. Our paid account will show the full hand calculations of how the tool got to this result. Refer below the calculator for more information on this topic, as well as links to other useful tools and features SkyCiv can offer you.
How to use the SkyCiv Moment of Inertia Calculator
Watch the video demo below to get started with our calculator.
Simply choose the cross-section shape you want to evaluate from the drop-down list, enter the dimensions of your chosen section and click Calculate.
This free multi-purpose calculator is taken from our full suite Structural Analysis Software. It allows you to:
- Calculate the Moment of Inertia (I) of a beam section (Second Moment of Area)
- Calculate the Centroid (C) in the X and Y axis of a beam section
- Calculate the First moment of area (Statical Moment of Inertia) (Q) of a beam section
- A Section Modulus Calculator to calculate the Section Modulus (Z) of a beam section
- Calculate the Torsion Constant (J) of a beam section
Common Section Property Definitions
The moment of inertia calculator will accurately calculate a number of important section properties used in structural engineering. Here is a concise list of the section property terms and definitions:
- Area of Section (A) – Section area is a fairly simple calculation, but directly used in axial stress calculations (the more cross section area, the more axial strength)
- Moment of Inertia (Iz, Iy) – also known as second moment of area, is a calculation used to determine the strength of a member and it’s resistance against deflection. The higher this number, the stronger the section. There are two axis here:
- Major Axis (Iz) – This is about the Z axis and is typically considered the major axis since it is usually the strongest direction of the member
- Minor Axis (Iy) – This is about the Y axis and is considered the minor or weak axis. This is because sections aren’t designed to take as much force about this axis
- Also worth noting that if a shape has the same dimensions in both directions (square, circular etc..) these values will be the same in both directions. See Moment of Ineria of a circle to learn more.
- Centroid (Cz, Cy) – this is the center of mass for the section and usually has a Z and Y component. For symmetrical shapes, this will be geometric center. For non-symmetrical shapes (such as angle, Channel) these will be in different locations. Learn how to calculate the centroid of a beam section. The above calculator also acts calculate the X and Y centroid of any type of shape.
- Statical Moment of Inertia (Qz, Qy) – Also known as First Moment of Area, this measures the distribution of a beam section’s area from an axis. Like the Moment of Inertia, these are in both the Z and Y direction. These are typically used in shear stress calculations, so the larger this value the stronger the section is against shearing. The calculator will provide this value, but click here to learn more about calculating the first moment of area.
- Elastic Section Modulus (Sz, Sy in America. Zz, Zy in Britain or Australia) – Also known as statical section modulus, and are used in bending stress calculations. They are usually calculated to the top and bottom fibres section. For instance, Szt is the section modulus about the Z axis to the top fibre of the section.
- Torsion Constant (J) – also known as the polar moment of inertia or J, is a value that describes a material's resistance to twisting or torsional deformation.
- The Plastic Section Modulus (S) – a measurement of the ability of a cross-section shape to resist plastic bending, used to estimate the stress of a material when it begins to yield (reach its plastic limit) under a specific load and is typically used for design and analysis of beams under load.
Other Parameters – These are more advanced results calculated by the full SkyCiv Section Builder:
- Product of Inertia (about Z and Y Axis): A measure of a shape's resistance to rotation about a specific axis, equal to the cross product of the distance from the axis to any point on the shape and the corresponding component of the point's moment of inertia.
- Plastic Section Modulus (about Z and Y Axis): A measure of the ability of a cross-section shape to resist plastic bending, used to estimate the stress of a material when it begins to yield (reach its plastic limit) under a specific load.
- Plastic Neutral Axis (about Z and Y Axis): An axis in a cross-section shape through which all forces acting on the shape must pass in order to result in plastic deformation.
- Shear Area (about Z and Y Axis): The area of a cross-section shape that is effective in resisting shear forces.
- Distance of Shear Centre to Centroid (in both Z and Y Axis): SkyCiv centroid calculator helps calculate the distance between the shear center and the centroid of a cross-section shape.
- Torsion Constant (Using FEA): A value that describes a material's resistance to twisting or torsional deformation, calculated using Finite Element Analysis.
- Torsion Radius: The distance from an axis at which the area of a cross-section shape must be concentrated to result in the same torsion constant as the actual shape.
- Warping Constant: A value that describes a material's resistance to warping or distortional deformation.
- Monosymmetry Constant (about Z and Y Axis): A measure of how symmetric a cross-section shape is about a specific axis, with a value of zero indicating perfect symmetry.
- Radius of Gyration (about Z and Y Axis): The distance from an axis at which the area of a cross-section shape must be concentrated to result in the same moment of inertia as the actual shape.
- Angle of Rotation of Principle Axis: The angle between the neutral axis and principal axis of a cross-section shape.
About Moment of Inertia, Centroids and other Section Properties
We've also compiled more information to calculating the moment of inertia of sections. This complete guide should help provide a comprehensive knowledge base for all things related to moment of inertia, centroids, section modulus and other important geometric section properties. In the below segments, we include what is moment of inertia, how to calculate the centroid, moment of inertia and common MOI equations with the help of SkyCiv Moment of Inertia and Centroid Calculator.
What is Moment of Inertia?
The Moment of Inertia (more technically known as the moment of inertia of area, or the second moment of area) is an important geometric property used in structural engineering. It is directly related to the amount of material strength your section has.
Generally speaking, the higher the moment of inertia, the more strength your section has, and consequently the less it will deflect under load. The Moment of Inertia of a rectangle, or any shape for that matter, is technically a measurement of how much torque is required to accelerate the mass about an axis - hence the word inertia in its name.
How to Find Moment of Inertia - Rectangular
To calculate the moment of inertia of a rectangle, you can use the formula:
I = (b * h^3) / 12
I is the moment of inertia of the rectangle
b is the width of the rectangle
h is the height of the rectangle
It is important to note that the unit of measurement for b and h must be consistent (e.g., inches, millimeters, etc.). Also The unit of the final result is depend on the input unit, for example if the input is in meter then the unit of result would be m^4.
Example Calculation of Moment of Inertia
Let's say we have a rectangle with the following dimensions:
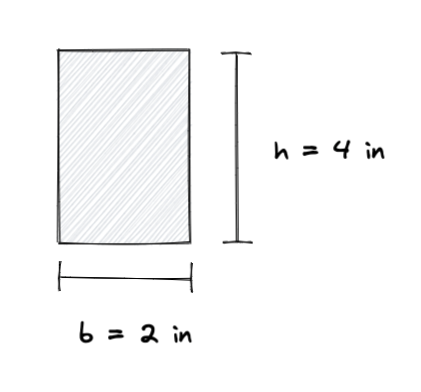
Using the formula for moment of inertia, we can calculate the moment of inertia of the rectangle as follows:
I = (b * h^3) / 12
I = (2 * 4^3) / 12
I = (2 * 64) / 12
= 10.67 in^4
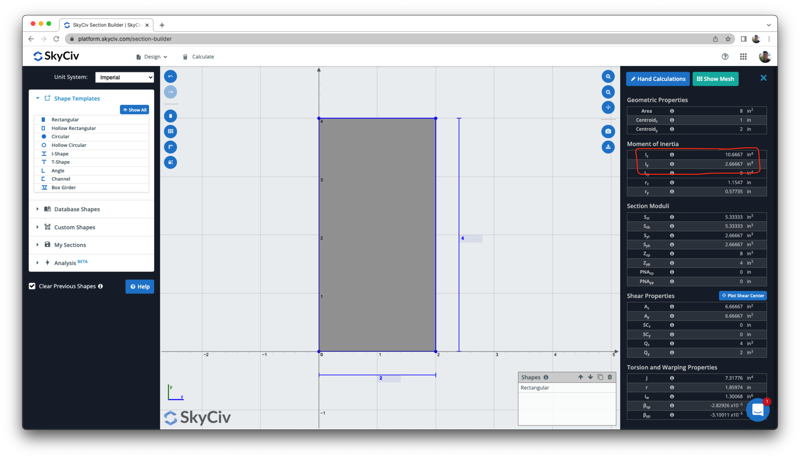
So the moment of inertia of the rectangle is 10.67 inch^4. This moment of inertia is about the centroidal axis, remember that if you need to find the moment of inertia about a different axis, you will need to use a different formula or perform a transformation. You can also check that unit is always the product of the power of input unit, in this case all input units are inches, so the result is in inches^4.
We can verify this result with the above free moment of inertia calculator, which shows the same result of 10.6667 in^4:
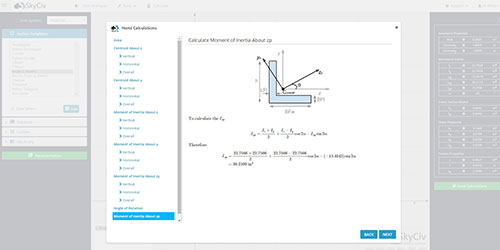
How to Find Moment of Inertia - I Beam
Now let's look at a more complex case of where the cross section is an I beam, with different flange dimensions. The concept is the same, however the approach in this case is quite different. Basically, we need to look at the I beam as a combination of different rectangles and sum the different parts to get the sections full Moment of Inertia. In short, we need to follow these three steps:
- Calculate the Neutral Axis for the entire section
- Calculate the MOI of each part
- Calculate the moment of inertia using the Parallel Axis Theorem - which is essentially the sum of individual moment of inertias
So let's consider the following section:
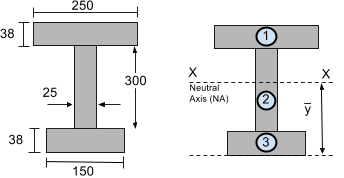
The The Neutral Axis (NA) is located at the centroid. This is essentially a weighted average of the area and distance from bottom for each segment. We simply need to use the centroid equation for calculating the vertical (y) centroid of a multi-segment shape.

We will take the datum or reference line from the bottom of the beam section. Now let's find Ai and yi for each segment of the I-beam section shown above so that the vertical or y centroid can be found.


Now we have the centroid. We can continue to calculate the moment of inertia. To calculate the total moment of inertia of the section we need to use the "Parallel Axis Theorem" as defined below:

Since we have split it into three rectangular parts, we must calculate the moment of inertia of each of these sections. We can now use the simplified rectangular moment of inertia formula:
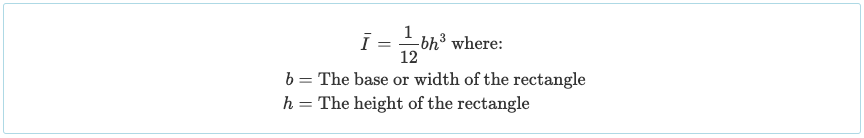
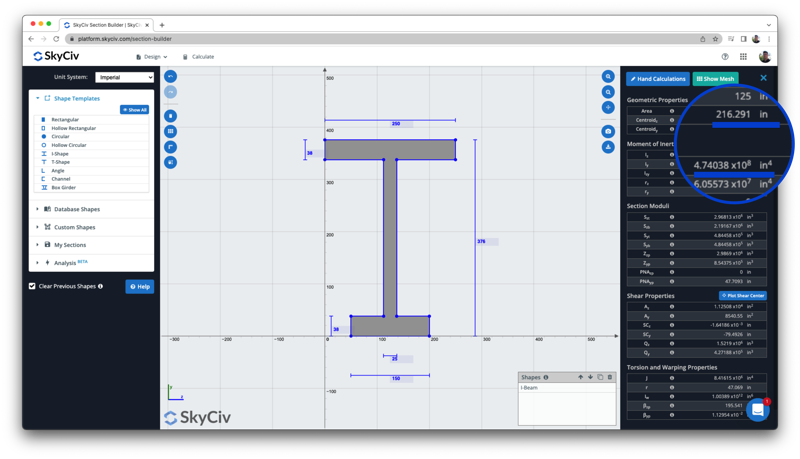
Now we have all the information we need to use the "Parallel Axis Theorem" and find the total moment of inertia of the I-beam section. In our moment of inertia example:

Once again, we can compare this result with that of the free moment inertia calculator to compare the results of both the centroid and moment of inertia, where both the centroid (216.29 in) and Moment of Inertia (4.74 x 10^8 in^4) match:
For more information, visit our tutorial on Calculating the Moment of Inertia of a Beam Section.
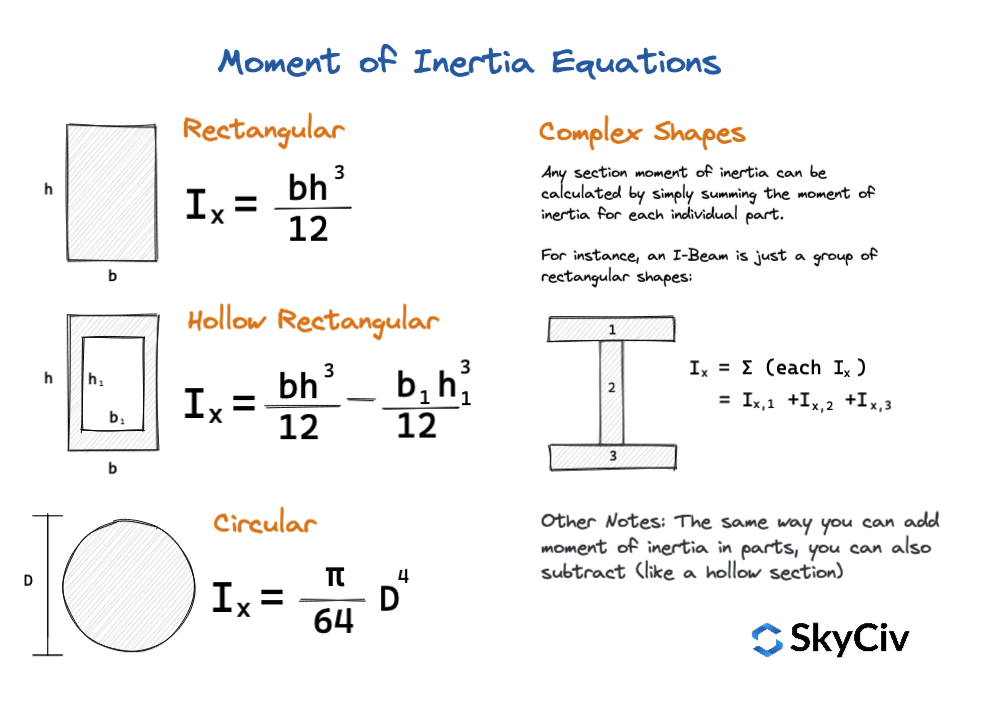
Moment of Inertia Equations
Simple equations can also be used to calculate the Moment of Inertia of common shapes and sections. These are quick moment of inertia equations that provide quick values and are a great way to cross reference or double check your results. Focusing on simple shapes only, the below diagram shows some of these equations:
SkyCiv Centroid Calculator
A centroid, also known as the 'geometric center', is the center of mass of an object with uniform density. A simplified demonstration of a centroid, would be the location at which you would need to place a pencil to make it balance on your finger. The location at which the pencil is balanced and does not fall off your finger would be the approximate location of the centroid of the pencil. It considers the mass and density of the material to determine the point where the mass of the pencil is equal on both sides of your finger, and therefore represents the 'center of mass' of the pencil.
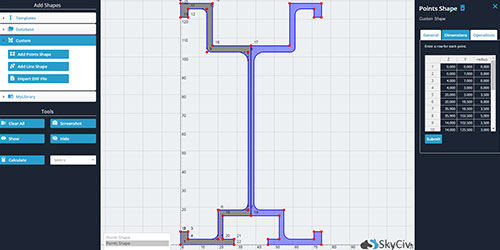
The SkyCiv Centroid Calculator uses FEA to provide highly accurate results in seconds, no matter how complex the shape. In the premium version, users can input the coordinates of the points that define the shape and our calculator will give you the coordinates of the centroid. This includes the ability to design custom shapes via DXF import, multiple (built-up) shapes and custom point shapes.
In addition to its speed and accuracy, our centroid calculator is also incredibly easy to use. With a simple user interface, you can input your section dimensions and receive your section property values (including the beam section centroid) within seconds. Whether you're working on a design project, experimenting with different sections or studying for an exam, the SkyCiv Centroid Calculator is the perfect tool to help you get the job done.
Section Modulus Calculator
As noted earlier, this free tool also provides you with a calculation of Elastic Section Modulus, however if you're starting out as an engineer you may not understand what the Section Modulus is. To put it simply, the section modulus is a section property of a cross-section that measures the resistance to bending and calculated as the ratio of the moment of inertia to the distance from the neutral axis to the most distant fiber. The Elastic Section Modulus is represented in this equation as simply:
Where,
- S is the section modulus
- I is the moment of inertia of the section about the neutral axis
- y is the distance from the neutral axis to the most distant point of the section
There are two kinds of Section Modulus: Elastic and Plastic. In America, S is typically used to refer to the Elastic Section Modulus while Z is used to refer to the Plastic Section Modulus. In Britain and Australia, these are typically reversed. Elastic Section Modulus is typically referred to with a letter Z, while the Plastic Section Modulus is referred to with a letter S.
In general, the Elastic Section Modulus is used for section design because it's applicable up to the yield point for most metals. Metals are not typically designed to go beyond the material's yield point.
Additional Documentation
Please refer to the following documentation pages for more detailed information on moment of inertia, how to calculate them for various shapes, and how to use our centroid calculator:
More Free Tools Available
SkyCiv also offers other tools such as I beam size tool and free structural design software. The dynamic section drawer will also show you a graphical representation of your beam section. So if you want to calculate the moment of inertia of circle, moment of inertia of a rectangle or any other shapes, feel free to use the below software or our all-inclusive SkyCiv Section Builder.
SkyCiv offers a wide range of Cloud Structural Analysis and Design Software for engineers. As a constantly evolving tech company, we're committed to innovating and challenging existing workflows to save engineers time in their work processes and designs.
Need More Functionality?
Upgrade to a professional plan to unlock full features