Moment of inertia is an important geometric property used in structural engineering. It is directly related to the amount of material strength your section has. Generally, a higher moment of inertia implies a greater strength in the section, resulting in reduced deflection when subjected to a load. The moment of inertia of a rectangle, or any shape for that matter, is technically a measurement of how much torque is required to accelerate the mass about an axis – hence the word inertia in its name.

Moment of Inertia of a Rectangle Formula

The general formula used when determining how to find the moment of inertia of a rectangle is:

[math] I_{xx}=\dfrac{BD^3}{12} , I_{yy}=\dfrac{B^3D}{12} [math]

Where the xx and yy refer to the particular axis, or direction, being considered.

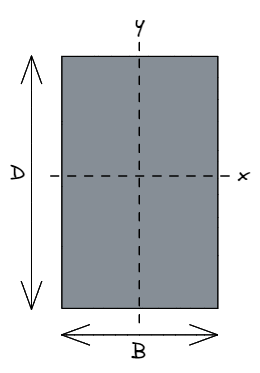
It is a common structural engineering convention that B refers to the width of the rectangle, parallel to a conventionally horizontal x-axis.

Similarly, D refers to the depth of the rectangle, parallel to a conventionally vertical y-axis.

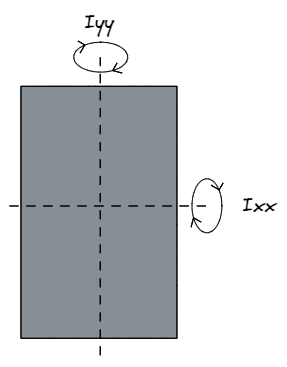
It may be confusing at first, but when structural engineers refer to Ixx they are in fact referencing the strength of a section about the x-axis, meaning in a direction parallel to the D dimension, or y-axis. Similarly, Iyy refers to the strength about the y-axis, meaning in a direction parallel to the B dimension, or x-axis.

Rectangular Hollow Sections (RHS)

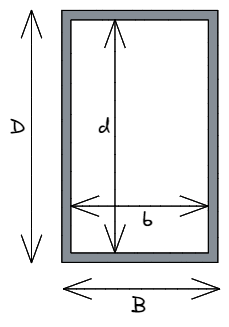
While engineers could hypothetically use solid rectangular sections when designing, this would use a significantly greater amount of raw material, with corresponding increases in weight and cost. It is much more common to use rectangular hollow sections (commonly referred to as an RHS). Here we can utilise the same equation defined above for the general rectangular case, however, we must subtract the inner hollow area of the rectangle:

[math] I_{xx}=\dfrac{BD^3}{12} – \dfrac{bd^3}{12} [math]

In this instance, lowercase b and d denote the size of the hollow area within the rectangle that we must subtract from the outer dimensions of the shape, being uppercase B and D. The difference between each corresponding dimension refers to the thickness of the material in that dimension – i.e. B – b = total thickness of the material parallel to the x-axis.

Besides the clear examples of weight and material use, why are hollow sections often described as more efficient than their solid counterparts?

Consider a beam undergoing a vertical load downwards. We expect the topmost fibres of the material to undergo a compressive force, while the corresponding bottom fibres will undergo a tensile force. The fibres along the neutral axis of the section (parallel to the section’s centroid) however, will experience neither compression nor tension, hence the name neutral axis.

Importantly, the magnitude of these compressive or tensile forces depend on the distance away from this neutral axis – material closer to the neutral axis needs to resist less force.

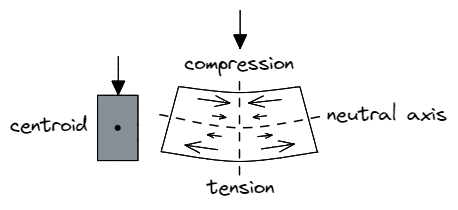
As such, the inner material of a fully solid section is resisting a relatively small amount of force while occupying a relatively large amount of area because the outermost material is working the hardest! Removing this inner part of the section and making it hollow consequently improves the efficiency of the section in regard to its weight, cost, and material use.

Conclusion

In summary, the formula for determining the moment of inertia of a rectangle is Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. For rectangular hollow sections, the formula is Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

The moment inertia is important for both bending moment force/stress and deflection. This is evident in their formulas, as in both cases, I (Moment of Inertia) is in the denominator:

Source: Bending Stress Formula

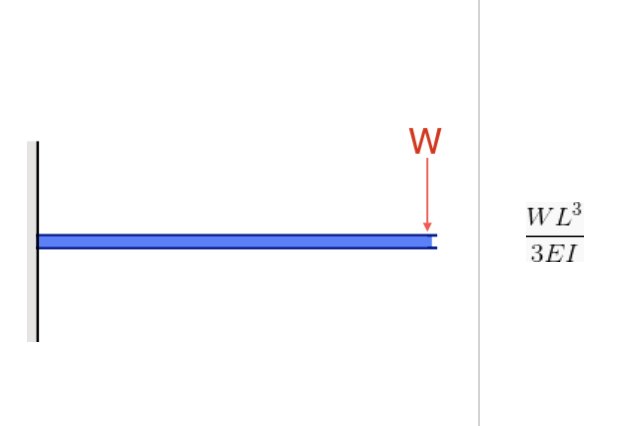
Source: Equation of Deflection in a Cantilever Beam

Moment of Inertia Calculator of a Circle

If you want to calculate the moment of inertia, check out our tutorial on the Moment of Inertia of a Circle to see how circular and rectangular section shapes compare with one another.

Free Moment of Inertia Calculator