Steel Base Plate Design Example Eurocode

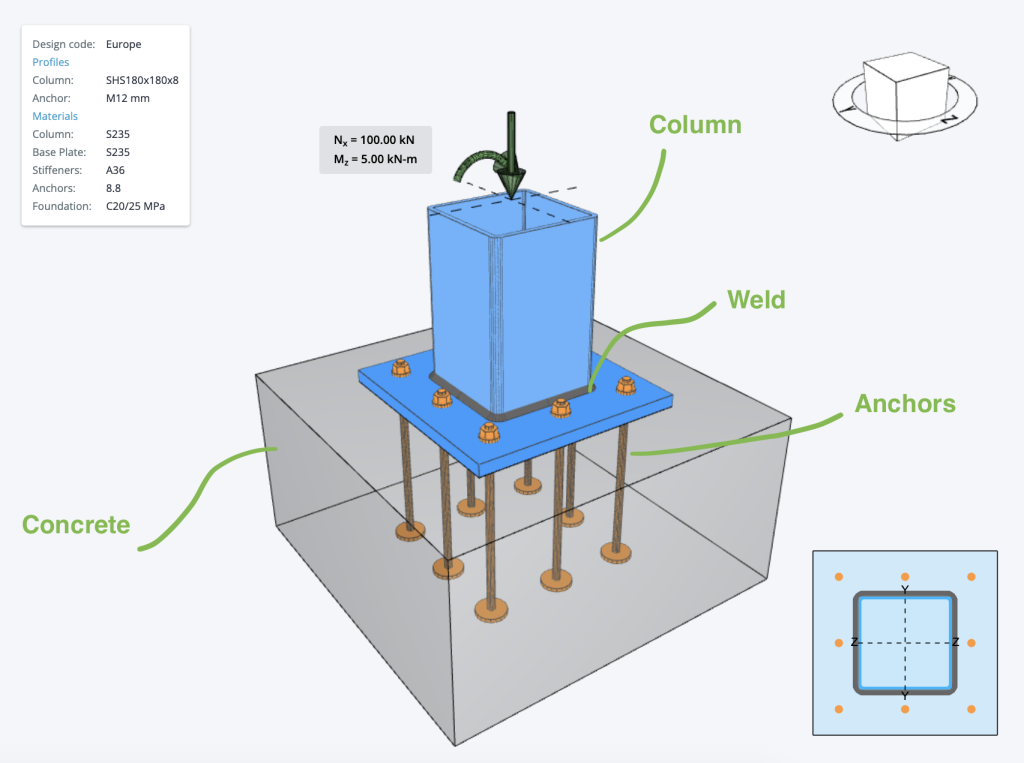
Below is an example of some Eurocode Base Plate Calculations that are commonly used in base plate design. Often when designing base plates, we will consider a few different checks relating to the various components of a base plate, namely:

• The Concrete base – generally checked against bearing and compression forces
• The Welds – welds need to be checked, to ensure they provide adequate restraint and do not fail under stress
• Anchor Bolts – can fail due to a number of reasons, as shown below in the example anchor bolt design calculations
• Steel Member (Column) checks – usually based on local steel design standards

Currently, the Steel Base Plate Design module implements the following checks below. The paid version of this software, includes detailed step-by-step calculations, so that engineers can review exactly how these calculations are made!

Try this calculation using SkyCiv Free Base Plate Calculator:

Base Plate Calculator

Concrete Capacity

The Steel Base Plate Design checks concrete bearing design in according to EN 1993-1-8 6.2.5 and shall satisfy:

\( F_{jd} = \alpha _{cc} \times \beta _{j} \times k_{j} \frac{f_{ck}}{\gamma _{c}} \)where:

• \( \alpha _{cc} \) – Long-term effects on Fcd
• \( \beta _{j} \) – Joint coefficient
• \( k_{j} \) – Concentration factor
• \( f_{ck} \) – Characteristic compressive concrete strength
• \( \gamma _{c} \) – Safety factor

 

Try this calculation using SkyCiv Free Base Plate Calculator:

Base Plate Calculator

 

Weld Capacity

The Steel Base Plate Design checks the weld design in according to EN 1993-1-8 4.5.3.2 and shall satisfy:

\( \omega_{w,Rd} = \frac{f_{u}}{ \beta_{w} \times \gamma _{M2} } \)and

\( \omega_{T,Rd} = 0.90 \times \frac{f_{u}}{ \gamma _{M2} } \)where:

• \( \omega_{w,Rd} \) – Equivalent stress resistance
• \( \omega_{T,Rd} \) – Equivalent stress resistance
• \( f_{u} \) – Utimate strength
• \( \beta _{w} \) – Appropriate correlation factor
• \( \gamma _{M2} \) – Safety factor

Try this calculation using SkyCiv Free Base Plate Calculator:

Base Plate Calculator

 

Anchor Bolts Capacity

The Steel Base Plate Design check the anchors capacity. Please see below base plate anchor bolt per Eurocode:

Bolt Strength in tension

A bolt subject to design tension force in Steel Base Plate Design is designed according to EN 1992-4 – Cl.7.2.1.3 and shall satisfy:

\( N_{Rk,s} = c \times A_{s} \times f_{uk} \)and

\( N_{Rd,s} = \frac{ N_{Rk,s} }{ \gamma _{Ms} } \)where:

• \( c \) = reduction factor for cut thread
• \( A_{s} \) – tensile stress area
• \( f_{uk} \) – Minimum yield strength of the bolt
• \( \gamma _{Ms} \) – Safety factor for steel

Bolt Strength in shear

A bolt subject to a design shear force in Steel Base Plate Design is designed according to EN1992-4 – Cl.7.2.2.3.1 and shall satisfy:

\( V_{Rk,s} = k_{7} \times V_{Rk,s}^{o} \)and

\( V_{Rd,s} = \frac{ V_{Rk,s} }{ \gamma _{Ms} } \)where:

• \( k_{6} \) – Coefficient for anchor resistance in shear
• \( k_{7} \) – Coefficient for anchor steel ductility
• \( A_{s} \) – tensile stress area
• \( f_{uk} \) – Minimum yield strength of the bolt
• \( V_{Rk,s}^{o} \) – the characteristic shear strength \( k_{6} \times A_{s} \times f_{uk} \)
• \( \gamma _{Ms} \) – Safety factor for steel

Anchor Breakout

A bolt subject to a design breakout in Steel Base Plate Design is designed according to AS5216:2018 and shall satisfy:

\( N_{Rk,c} = N_{Rk,c}^{o} \times \frac{A_{c,N}}{A_{c,N}^{o}} \times \phi _{s,N} \times \phi _{re,N} \times \phi _{ec,N} \times \phi _{M,N} \)and

\( N_{Rd,c} = \frac{ N_{Rk,c} }{ \gamma _{Mc} } \)where:

• \( N_{Rk,c}^{o} \) – Characteristic strength of a fastener, remote from the effects of adjacent fasteners or edges of the concrete member.
• \( A_{c,N} \) – Concrete breakout cone area for group of anchors.
• \( A_{c,N}^{o} \) – Concrete breakout cone area for single anchor not influenced by edges.
• \( \phi _{s,N} \) – Parameter related to the distribution of stresses in the concrete due to the proximity of the fastener to an edge of the concrete member.
• \( \phi _{re,N} \) – Parameter accounting for the shell spalling.
• \( \phi _{ec,N} \) – Modification factor for anchor groups loaded eccentrically in tension.
• \( \phi _{M,N} \) – Parameter accounting for the effect of a compression force between the fixture and concrete.
• \( \gamma _{Mc} \) – Safety factor for concrete.

Concrete pryout

A bolt subject to design tension force is designed according to EN1992-4 – Cl. 7.2.2.4 and shall satisfy:

\( V_{Rk,cp} = k_{s} \times N_{Rk,c} \)
and

\( V_{Rd,cp} = \frac{ V_{Rk,cp} }{ \gamma _{Mc} } \)
where:

• \( k_{s} \) – Parameter published in the Report of Assessment
• \( N_{Rk,c} \) – Characteristic concrete cone strength for a single fastener or fastener in a group
• \( \gamma _{Mc} \) – Safety factor for concrete.

Anchor Bolts Utility ratio Checks

Utility ratio for steel

Interaction of tensile and shear forces of steel in reference of EN 1992-4 – Table 7.3

\( \left( \frac{ N_{Ed} }{ N_{Rd,s} } \right)^{2} + \left( \frac{ V_{Ed} }{ V_{Rd,s} } \right)^{2} \leq 1.0 \)

Utility ratio for concrete

Interaction of tensile and shear forces in concrete in reference of EN 1992-4 – Table 7.3

\( \left( \frac{ N_{Ed} }{ N_{Rd,s} } \right)^{1.5} + \left( \frac{ V_{Ed} }{ V_{Rd,s} } \right)^{1.5} \leq 1.0 \)

 

Try this calculation using SkyCiv Free Base Plate Calculator:

Base Plate Calculator