General description
SkyCiv has a robust and advanced module for reinforced concrete slab design. To access this feature, you must have first built a model on SkyCiv S3D and then call the module for automatic calculation with different construction codes such as ACI-318, European and Australian Standards, and so on. The module’s primary purpose for plate design is to provide the steel reinforcement rebar quantity along the plate.
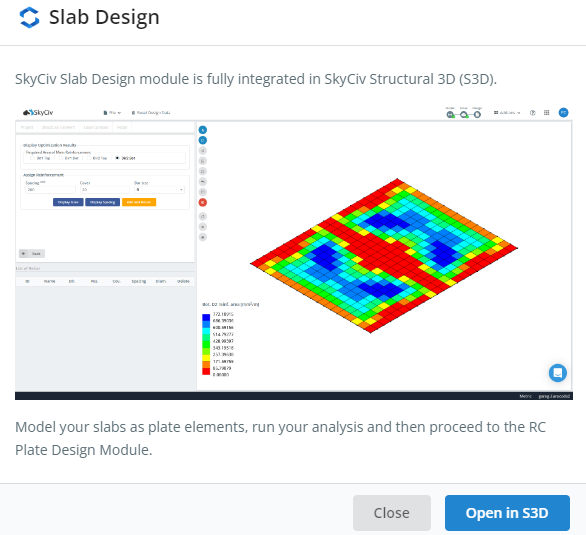
Figure 1. SkyCiv Slab Design Module
If you are new at SkyCiv, Sign up and test the software yourself!
SkyCiv documentation provides excellent content, including examples and cases of analysis, both for learning if you are new to the modules and for comparing the results from the plate design module with hand calculations. Feel free to check our design examples according to ACI-318, Eurocode, and AS3600.
We suggest you read this article before deeply analyzing complex slab systems. Here, you will learn how the bending moments differ depending on slab plan dimensions. There are two cases of study, one-way and two-way slabs. So, let’s start reading!
One-way versus two-way slab behavior
Let’s consider the slab example in the following image, where there is support on each slab edge, and we establish this will behave as a two-way plate, that is, having a bending moment in the two principal plan directions.
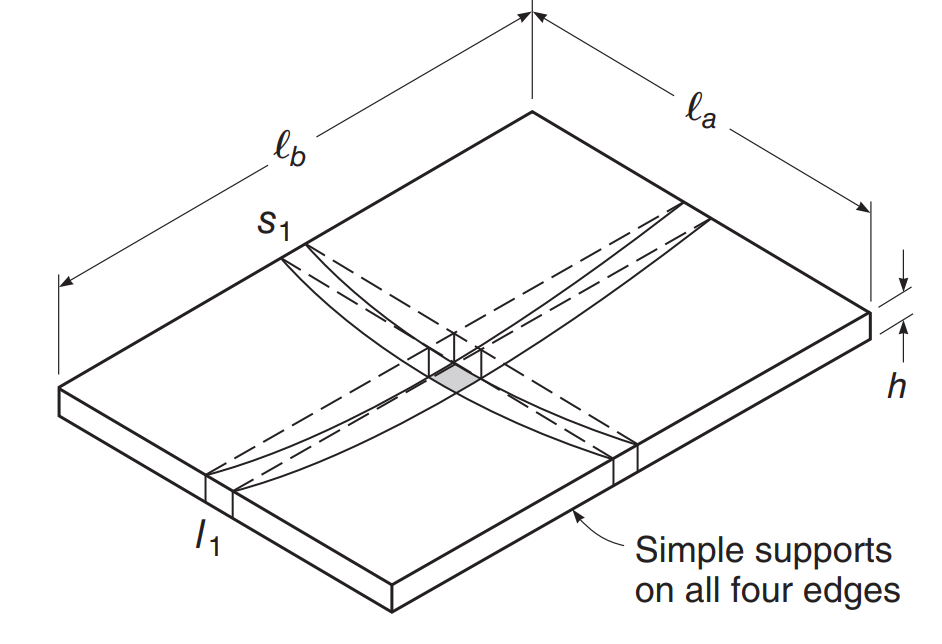
Figure 2. Simple two-way slab example on bending. (David Darwin, Charles W.Dolan, Arthur H. Nilson, “Design of Concrete Structures,” Fifteenth Edition, McGraw-Hill Education)
We can define the vertical displacement as (\(l_a < l_b \)):
\(\Delta_a = \frac{{5}{w_a}{l_a^4}}{384{E}{I}}\)
\(\Delta_b = \frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
Due to the slab being a continuous system, both vertical deflections will have the same value. We can compare the equations to express a relation between the load being carried by each direction as a function of the plan dimensions.
\(\Delta_a = \Delta_b \to \frac{{5}{w_a}{l_a^4}}{384{E}{I}} = \frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
\(\frac{w_a}{w_b} = {(\frac{l_b}{l_a}})^4 \)
All reinforced concrete references for slab design divide into one-way and two-way if the quotient of \(\frac{l_b}{l_a}\) is greater or less than a value of 2, respectively.
Using the above equations, when \(\frac{l_b}{l_a}=2\), the load carried by short direction is equal to \(w_a = {16}{w_b}\) and when the value is \(\frac{l_b}{l_a}=1\), the load is distributed equally in both directions \(w_a ={w_b}\).
One-way slabs moments
So, we can see that when the quotient of dimensions is greater than 2, practically, all the loads and bending moments will be concentrated only in the short direction. This case is the one-way slab behavior, and the maximum bending moment can be obtained as a simply supported beam with a unitary width.
\(M_{max,1,D}=\frac{{w_a}{1 m}{l_a^2}}{8}\)
Two-way slabs moments
The solution of the case of the two-way slab is a complex and challenging problem in structural mechanics. You can see in the figure below the general analysis consists of a plate with entire forces and moments in each direction.
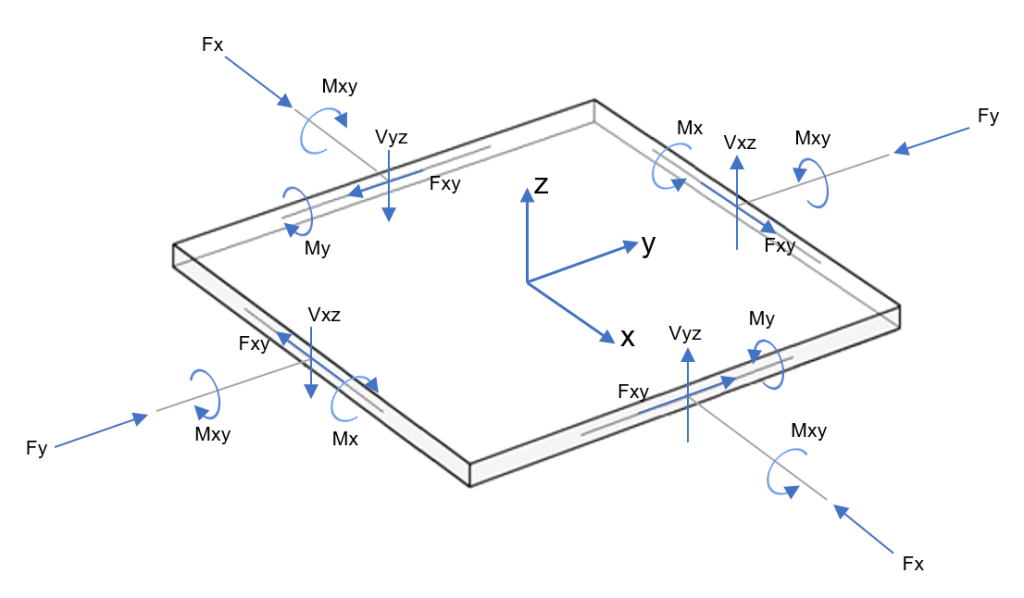
Figure 3. Actions on plate element (bending and torsional moments; normal and shear forces)
This difficulty comes from the actual problem to solve is a fourth-order partial differential equation that involves the bending in two directions. The shape of this equation is:
\(\frac{\partial^4{w}}{{\partial}{x^4}} + {2}\frac{{\partial^4}{w}}{{{\partial}{x^2}}{{\partial}{y^2}}}+\frac{\partial^4{w}}{{\partial}{x^4}}-\frac{f_z}{D} = 0\)
Where the plate stiffness (using the elastic mechanical and geometric properties) is \(D=\frac{{E}{t^3}}{{12}{(1-\nu^2)}}\).
The analytical solution of this equation is only available for straightforward support conditions. The only way to obtain a possible solution for practical and actual live cases is through numerical methods such as the Finite Element Method.
SkyCiv uses this approach to solve plate analysis. On the following links, you will have access to tutorials to learn about SkyCiv platform characteristics: Plate Design in S3D and How to model plates? .
If you are new at SkyCiv, Sign up and test the software yourself!

