
Support Configuration
The most common way that structural engineers classify beams is by their support configuration, there are many possible configurations however, these are the 5 most common types:
Simply Supported Beam

Simply supported beams are defined as having two supports at either end – one pinned and one roller. This is generally considered as being the most simple type of beam. This is a very common type of beam and is determinate because there are three equilibrium equations and only 3 unknown reactions. 2 from the pinned support and 1 from the roller support.
Cantilever Beam

Cantilever beams are supported from one end, using a fixed support. This is the only type of support that can be used in this scenario as it offers the moment resistance required for the beam to remain stable. If a pinned or roller support was used, it would not offer the moment restraint that the beam would need. A good example of a cantilever beam is a shop awning – where the beam is bolted directly into the wall. This is also a determinate beam because there are only 3 unknown reactions which, is equal to the number of equilibrium equations available.
Check out SkyCiv’s Free Beam Calculator
Continuous Beam
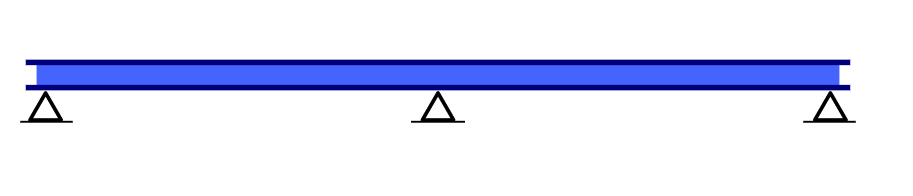
Continuous beams are multi-spanned beams that have multiple supports across the length of the beam. An example of a continuous beam would be a single beam that is supported by a number of columns along its length. This beam is indeterminate since there are more unknown reactions (6) than equilibrium equations available (3). This is then called a level 3 indeterminate beam.
Fixed Beam

Fixed beams have fixed supports at either end – offering moment resistance at either end. This type of beam may be used when the designer wants to control the deflection at the mid-span because the two fixed supports prevent rotation. This beam is also indeterminate as the unknown reactions (6) are greater than the equations available (3). This is also a level 3 indeterminate beam.
Overhanging Beam

Overhanging beams are those with two supports, but unlike simply supported beams, one of the supports is not at the end of the member. A typical example of this is a balcony that is being extended from a frame structure. The frame offers the two supports, yet no support exists at the end of the member – allowing it to ‘overhang’ as the name suggests. This too is an indeterminate beam as the number of unknown reactions (4) is greater than equilibrium equations (3). This is a level 1 indeterminate beam.
Overhanging Beam
Learn more about beams with our beam tutorial series, covering topics such as:
- Cantilever beams
- Deflection formula
- Bending moment
- Shear force diagrams
- Intermediate beams
- Determining reactions at supports
SkyCiv Beam Software
SkyCiv Beam Analysis Software allows users to analyze beam structures easily and accurately. You can get a simplified analysis of your beam member, including reactions, shear force, bending moment, deflection, stresses, and indeterminate beams in a matter of seconds.
If you want to give it a try first, Free Online Beam Calculator is a great way to start, or simply sign up for free today!


