Calculating Lateral Earth Pressure on a Retaining Wall
One of the main loads acting on a retaining wall is the lateral earth pressure. For that reason, doing a good estimation of its magnitude and distribution is decisive in the design of a Concrete Retaining Wall. In general, there are three different types of lateral earth pressure depending on the direction that the wall tends to move:
- At-rest earth pressure: When the wall is completely restrained from moving
- Active earth pressure: When the wall may tilt away from the retained soil
- Passive earth pressure: When the wall may be pushed into the retained soil
In this article, we will focus on describing the formulas for each of the earth pressure cases mentioned above.
Lateral earth pressure distribution
In general, lateral earth pressure behaves the same as hydrostatic pressure. Having a zero value at the surface and a maximum value at the deepest point following a linear distribution between the two mentioned boundaries. Therefore, the horizontal subsurface stress distribution is described by the following expression:
\(\sigma_h = K_* \cdot (\gamma z)\)
Where \(K_*\) takes the value of \(K_o\) for the case of at-rest pressure, \(K_a\) for the case of active pressure, and \(K_p\) for the case of passive pressure.
Integrating the given expression for the lateral subsurface stress from \(0\) to \(H\) in \(z\), the resultant turns out to be:
\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)
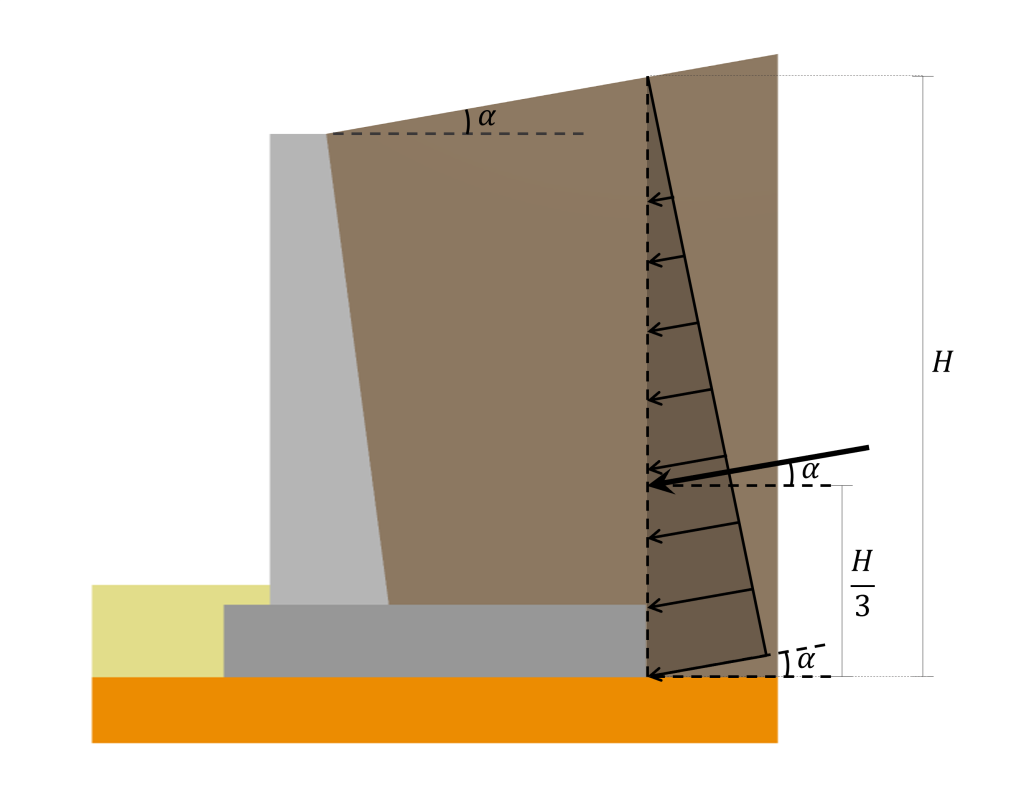
This resultant’s line of action is located \(\frac{2}{3}H\) from the surface. The lateral earth pressure distribution, its resultant, and location described above are illustrated in the following picture:
It is important to mention that the presented distribution and resultant calculation approach only applies to soil pressures acting on a vertical backface. In the case of a retaining wall with an inclined backface (like the one in the picture above), the surface where the soil pressure acts is still considered vertical since it is assumed to act in a vertical plane located where the heel ends.
Additionally, when the backfill is inclined at some angle \(\alpha\) with respect to the horizontal, the pressure distribution and its resultant are inclined at that same angle \(\alpha\) as illustrated in the following:
Correctly estimating the lateral earth pressure distribution and its resultant is a crucial step in the Retaining Wall Design Process. For more information about how this lateral earth pressure is included in the Retaining Wall Design Process, refer to the article here. Let’s now dive into the formulas for calculating the resultant lateral earth pressure exerted on a Retaining Wall by the soil in different conditions.
At-rest lateral earth pressure
This approach for calculating the lateral earth pressure against a Retaining Wall can only be used if the wall is completely at rest and is not allowed to move either away from the soil or into the soil, this condition ensures that the horizontal strain in the soil is zero. For this case, the coefficient of at-rest pressure (\(K_o\)) is the one that replaces \(K_*\) in the previous equations. That coefficient is the only unknown for calculating the pressure distribution and its resultant. For normally consolidated soil, the relation for \(K_o\) is:
\(K_o = 1-sin(\phi’)\)
Where \(\phi’\) is the effective angle of friction of the soil in consideration.
For overconsolidated soil, the coefficient may be calculated using the following expression:
\(K_o = (1-sin(\phi’))\cdot OCR^{sin(\phi’)}\)
Where \(\phi’\) is the effective angle of friction, and \(OCR\) the overconsolidation ratio of the soil in consideration.
Plugging this coefficient into the expression for calculating the resultant force from the lateral earth pressure at-rest yields to:
\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)
Active lateral earth pressure
The previous approach can be used when the wall does not yield at all, however, if a wall tends to move away from the soil, the soil pressure on the wall at any depth will decrease. For this case, the coefficient of active pressure (\(K_a\)) is the one that replaces \(K_*\) in the initial equations. Using Rankine’s approach for a granular backfill, and assuming that the pressure acts in a vertical backface, the active earth-pressure coefficient may be calculated using the equation:
\(K_a=cos(\alpha) \frac{cos(\alpha) – \sqrt{cos^2(\alpha) – cos^2(\phi’)}}{cos(\alpha) + \sqrt{cos^2(\alpha) – cos^2(\phi’)}}\)
Where \(\phi’\) is the angle of friction of the soil in consideration and \(\alpha\) is the angle of inclination of the backfill surface with respect to the horizontal.
Plugging this coefficient into the expression for calculating the resultant force from the lateral earth pressure at active condition yields to:
\(P_a=\frac{1}{2} \gamma \cdot H^2 \cdot K_a\)
The Rankine active pressure calculations presented before are based on the assumption that the wall is frictionless.
Passive lateral earth pressure
The lateral earth pressure acting on a retaining wall is considered passive when the wall is pushed into the soil mass, in that condition, the horizontal stress will increase with respect to the at-rest condition. For this case, the coefficient of passive pressure (\(K_p\)) is the one that replaces \(K_*\) in the initial equations. Using Rankine’s approach for a granular backfill, and assuming that the pressure acts in a vertical backface, the passive earth-pressure coefficient may be calculated using the expressions:
When the backfill is completely horizontal
\(K_p = tan^2(45º+\frac{\phi’}{2})\)
When the backfill is inclined a certain angle with respect to the horizontal
\(K_p=cos(\alpha) \frac{cos(\alpha) + \sqrt{cos^2(\alpha) – cos^2(\phi’)}}{cos(\alpha) – \sqrt{cos^2(\alpha) – cos^2(\phi’)}}\)
Where \(\phi’\) is the angle of friction of the soil in consideration and \(\alpha\) is the angle of inclination of the backfill surface with respect to the horizontal.
Plugging this coefficient into the expression for calculating the resultant force from the lateral earth pressure at passive condition yields to:
\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)
Again, the Rankine active pressure calculations presented before are based on the assumption that the wall is frictionless.
References
Retaining Wall Calculator
SkyCiv offers a free Retaining Wall Calculator that will calculate the lateral earth pressure on the wall, and perform a stability analysis on your retaining walls. The paid version also displays the full calculations, so you can see step by step, how to calculate the stability of a retaining wall against overturning, sliding, and bearing!
Product Developer
BEng (Civil)