Moment of Inertia is an important geometric property used in structural engineering, as it is directly related to the amount of material strength your section has. Generally speaking, the higher the moment of inertia, the more strength it has and the less it will deflect under load. The Moment of Inertia of a circle, or any shape for that matter, is essentially how much torque is required to rotate the mass about an axis – hence the word inertia in its name. Note, this is not to be confused with Moment Area of Inertia (Second moment of inertia) which is a different calculation and value altogether.

Moment of Inertia of a Circle Formula

Another useful exercise is to look at this all by considering the general moment of inertia circle formula:

[math] I_{x}, I_{y}=\dfrac{\pi}{64}D^4 [math]

And the moment of inertia formula for hollow circular sections:

[math] I_{x}, I_{y}=\dfrac{\pi}{64}D^4 – \dfrac{\pi}{64}d^4 [math]

Evidently, we can see that some of the moment of inertia is removed from the cutout. However, because this is not providing much restraint against bending (given it’s so close to the centroid), it is an inefficient use of material. So removing this part of the section actually improves the efficiency of the section.

Moment of Inertia of a Circle – A detailed breakdown

The moment inertia is important for both Bending Moment Force/Stress and Deflection. This is evident considering their formula, wherein in both cases, I (Moment of Inertia) is in the denominator:

Source: Bending Stress Formula

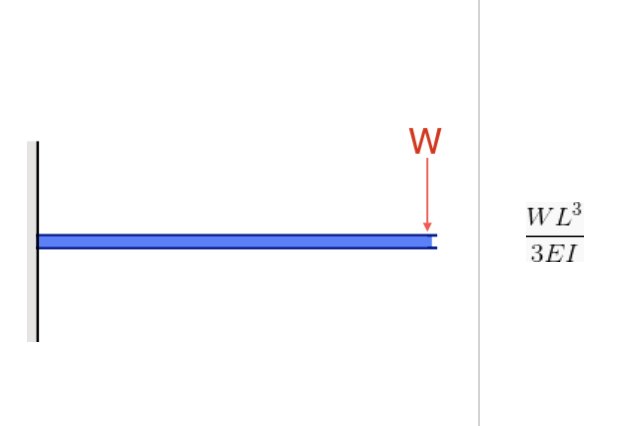
Source: Equation of Deflection in a Cantilever Beam

Moment of Inertia in circular cross sections has a particular behavior. Firstly, they have the same moment of inertia in both axis (known as major and minor axis). This makes sense as the section is symmetrical in both the X and Y directions. We’ll look at how this is not always the case in other sections, when we compare with an I beam below. However, this can be a benefit when loading is not always along the member’s strong axis, as you can predict the strength of the member regardless of the load direction. Despite this, circular sections typically don’t have a very high moment of inertia values for their weight (in comparison to say an I beam for instance) as we’ll learn more in the next session.

Pros and Cons of Circular Sections

It’s interesting to compare the moment of inertia of a circle compared to other shapes, to really understand how it behaves differently. For one, most of the mass is concentrated around the centroid, with not as much mass at the top and bottom. This is pretty important for moment of inertia calculations, since the further away the mass, the higher the value. Let’s look at a comparison, produced by SkyCiv Section Builder:

Moment of Inertia Calculator

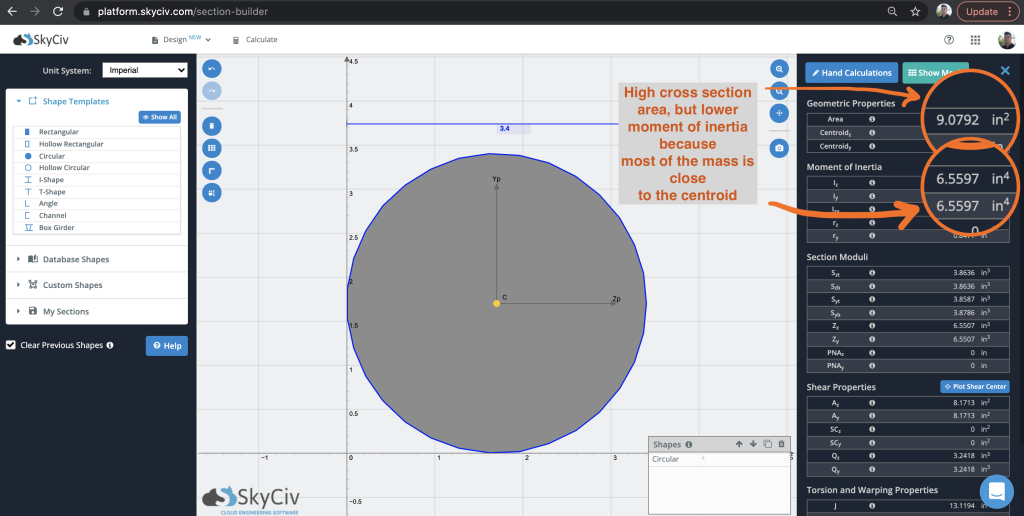
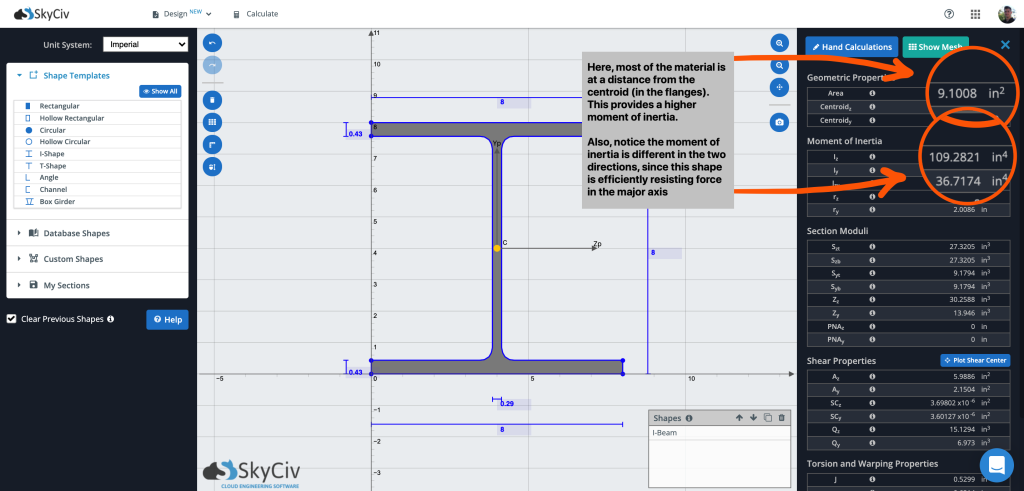
So in the above, we have roughly 9 square inches of material providing a moment of inertia of 6.5597. We can also see that the Iy and Iz values are the same because the section is symmetrical in both directions, as previously mentioned. When comparing this to an I-Beam with the same area, we can see the difference of having most of our mass further away from the centroid:

Moment of Inertia of a Hollow Circular Section

Given this behaviour, this is often why we don’t see many solid circular sections in structural engineering and are often replaced with more favourable Hollow Circular sections. These are more efficient at providing a higher moment of inertia values for the same reason as the I beam: most of the mass is at a distance from the centroid. Consider a hollow circular shape with a similar area:

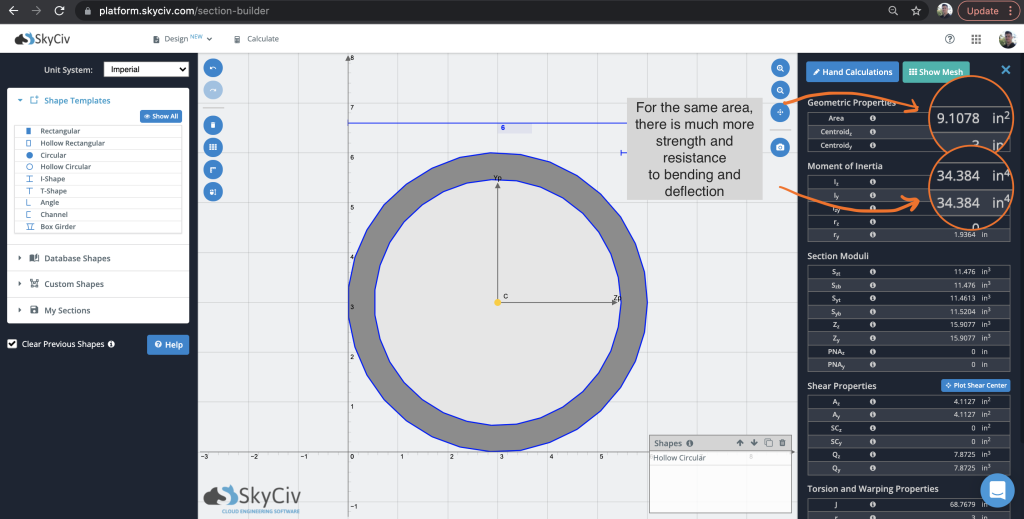
So, in summary for the same material as a solid circular section, the moment of inertia is over 5 times stronger. This plays a critical role in the strength against bending moment force and deflection.