When running a Response Spectrum Analysis on a structure, one of the most important steps for getting the desired results is the definition of the modal combination method that will be used by the software to get a single result for displacement, reactions, internal forces, etc… for each degree of freedom out of the raw results obtained for each vibration mode (modal responses). Those modal combined results are the ones used for designing the structure, that’s why properly defining the modal combination method is extremely important. In this article, we will dive into some modal combination methods for Response Spectrum Analysis.
It is important to mention that one of the most important steps during a Response Spectrum Analysis is the evaluation of the natural frequency for each vibration mode and its mass contribution, check our documentation on Dynamic Frequency Analysis.
Modal Combination Methods for Response Spectrum Analysis
Some of the most known and used methods for modal combination are:
- ABS: Absolute Sum
- SRSS: Square Root of Sum of the Squares
- CQC: Complete Quadratic Combination
In general, peak values of the total response (\(r_o\)) for displacements, internal forces, and reactions are of interest. As mentioned before, that peak value is obtained from properly combining the peak modal responses (\(r_{n, o}\))
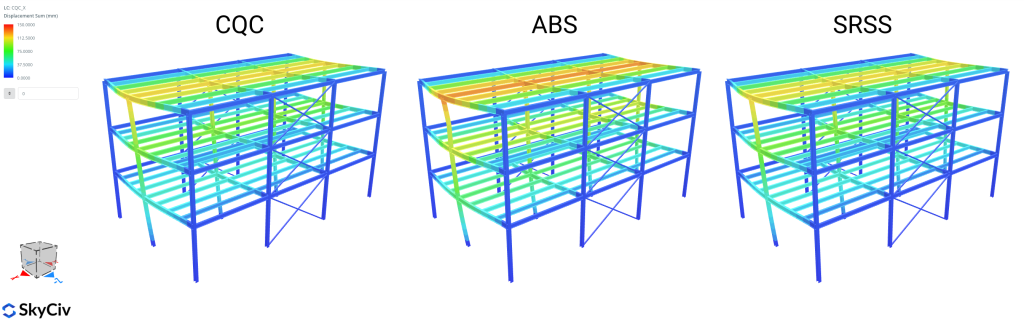
Absolute Sum (ABS)
The Absolute Sum modal combination method takes the absolute value of the result (displacement or internal force) for each vibration mode and sums up all those absolute values. Physically, it assumes that all the peak modal responses occur at the same time. By doing that, it is the most conservative method, as it makes every modal contribution positive, and therefore, it is not popular in structural design applications. The formula for calculating the peak value of the total response is:
\(r_o=\sum_{n=1}^{N} |r_{n,o}|\)
Where,
\(n\) is the \(n^{th}\) vibration mode considered in the analysis
\(N\) is the total number of vibration modes considered in the analysis
\(r_o\) is the peak total response
\(r_{n,o}\) is the peak modal response for the \(n^{th}\) vibration mode
Square Root of Sum of the Squares (SRSS)
The Square Root of the Sum of the Squares modal combination method takes the square root of the sum of the squares of the result for each vibration mode, providing an estimate of the peak of the total response. This modal combination method provides excellent response estimates for structures with well-separated natural frequencies, for the cases in which the natural frequencies of the structure are not well-separated this method should not be used. Formally, the peak total response can be expressed as follows:
\(r_o=\left(\sum_{n=1}^{N} r^{2}_{n,o}\right)^{1/2}\)
Where,
\(n\) is the \(n^{th}\) vibration mode considered in the analysis
\(N\) is the total number of vibration modes considered in the analysis
\(r_o\) is the peak total response
\(r_{n,o}\) is the peak modal response for the \(n^{th}\) vibration mode
Complete Quadratic Combination (CQC)
The Complete Quadratic Combination method overcomes the limitation mentioned for SRSS when combining modal responses in a structure with closely-spaced natural frequencies. In this method, the peak total response is obtained by applying the following formula:
\(r_o=\left(\sum_{i=1}^{N}\sum_{n=1}^{N} \rho_{in} \cdot r_{io} \cdot r_{no} \right)^{1/2}\)
Where,
\(n, \; i\) is the \(n^{th}, \; i^{th}\) vibration mode considered in the analysis
\(N\) is the total number of vibration modes considered in the analysis
\(r_o\) is the peak total response
\(r_{n,o}, \; r_{i,o}\) is the peak modal response for the \(n^{th}, \; i^{th}\) vibration mode
\(\rho_{in}\) is the correlation coefficient for the two modes being combined at each summation step
The formula above can be rewritten as two separate groups of summations, the first being identical to the SRSS modal combination method. The second double summation includes all the cross (\(i \neq n\)) terms, each of which may be positive or negative, this yields the fact that the estimate for the peak total response using CQC might be larger or smaller than the estimate provided by the SRSS :
\(r_o=\left( \sum_{n=1}^{N} r^{2}_{n,o} + \underbrace{\sum_{i=1}^{N}\sum_{n=1}^{N}}_{i \neq n} \rho_{in} \cdot r_{io} \cdot r_{no} \right)^{1/2}\)
Only one term in the equation for CQC has not been defined: the correlation coefficient. One of the most used equations for this coefficient is:
\(\rho_{in} = \frac{\xi^2(1+\beta_{in})^2}{(1-\beta_{in})^2+4\xi^2\beta_{in}}\)
Where,
\(\beta_{in}\) is the ratio between the natural frequencies of the \(i^{th}\) and \(n^{th}\) modes (\(\omega_i / \omega_n\))
\(\xi\) is the damping coefficient for the structure
References
Chopra, A. (2015, June 4). Dynamics of Structures (4th ed.). Pearson Higher Education.
New to SkyCiv Structural 3D? Sign up today for FREE!
Product Developer
BEng (Civil)


