How to Check if a Column is Buckling
In this short tutorial, we’ll go through everything you need to know about simple column buckling analysis. As we all know, columns are vertical members in a structure that experience high compressive axial loads. Members that are subjected to compressive loads may experience a failure method called “Buckling” which is described as sudden sideways deflection. It is different from yielding, but we’ll explain this throughout the tutorial.
Euler Buckling Theory
The mathematician Leonhard Euler investigated the behavior of columns and derived a simple formula for the load required to buckle a column. This is called the critical buckling load:

This is a fairly straightforward formula, however, there are some important things to note. Firstly, a member’s cross-section has two moments of inertia values (Iz and Iy), so which one should you choose? Well since the formula is concerned with finding the critical buckling load then it’s clear that we should take the lowest moment of inertia of the section since that will yield the lowest critical buckling load (i.e. it will buckle sooner). Secondly, rather than using the actual length of the member, L, we instead use the effective length of the column, KL. So what is this K factor and why is it necessary? We’ll discuss this in the next section.
Effective Length Factors (K)
Euler was a smart fellow and he quickly figured out that the length of the column needs adjusting based on how it is constrained or supported on either end. For this reason, we can use a factor, K which adjusts the length to give KL. The theoretical and recommended values for the effective length factor (K) are provided in the diagram below:
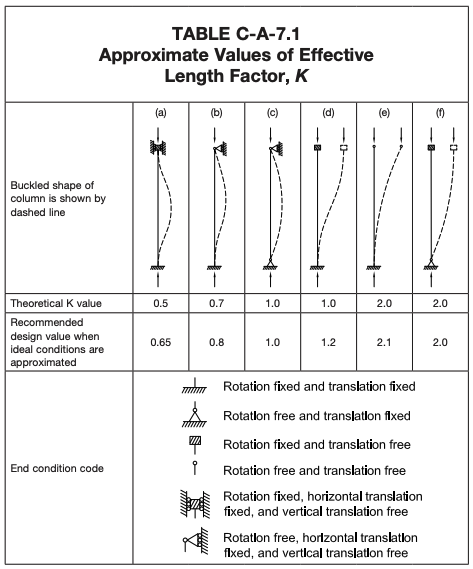
Source: AISC 360-22: Specification for Structural Steel Buildings
Buckling vs Yielding
Buckling and yielding are two different forms of failure. Yielding occurs when a member’s stress exceeds the material’s yield strength. However, buckling may occur before yielding occurs depending on the column’s situation. For instance, if the columns’ critical buckling load was 20 kN and its area was only 1000 mm2 then its critical buckling stress would be:
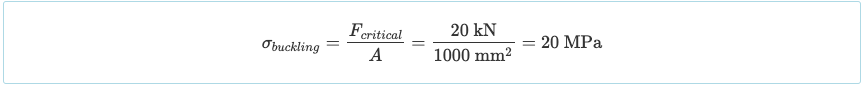
Since the critical buckling stress is lower than the yield strength of the material (say 300 MPa), then it would buckle before it yields.
Column Buckling Example
Let’s use this knowledge to do an example:
Let’s say I have a 100x20x3mm RHS column which is made of structural steel (E = 200 GPa). If it has a length of 3.0 meters and is fixed at the base and pinned at the top, at what theoretical load will it begin to buckle?
Using our Free Moment of Inertia Calculator we can see that the lowest moment of inertia of the RHS cross-section is I = 45,172 mm4. For structural steel E = 200 GPa = 200 kN/mm2. Using the table above we can see that the effective length factor for a fixed-pinned column is K = 0.7 and of course L = 3.0 m = 3000 mm. Therefore we can use Euler’s Buckling Formula:

So once the compressive axial force on the member reaches 20.22 kN and over the member will theoretically buckle!
I hope this tutorial has helped you understand more about how to simply calculate column buckling. Check out our free Column Buckling Calculator, Column Calculator or sign up today to get started with SkyCiv software!


