FREE TOOLS
Column Buckling Calculator
The SkyCiv Column Buckling Calculator is a free resource to help engineers complete buckling analysis for centrally loaded compression members. Columns are vertical load-bearing members that transfer weight from higher structures to lower ones. Because of this, columns experience high compressive loads that make them subject to failure due to buckling. Buckling occurs when the column exceeds its critical load. When loaded with a force greater than its critical load the column may experience buckling failure where it deforms with a sudden sideways deflection. This buckling load calculator allows engineers to determine the critical load of column-based members depending on factors including the slenderness ratios of the column and the columns length, cross-section, material, and boundary conditions. This column buckling calculator can help engineers ensure that the loads on their columns are not more than the critical buckling load.
About this Column Buckling Calculator
How is critical buckling calculated?
The critical load of a column member is determined by factors including the column’s length, cross-section, material, and boundary conditions. Two formulas are used to calculate column buckling in the buckling calculator depending on the slenderness ratios of the column:
- Euler’s Formula for Column Buckling is used when the Slenderness Ratio of the column member is greater than the Critical Slenderness Ratio.
- Johnson’s Parabolic Formula for Column Buckling is used when the Slenderness Ratio of the column member is less than the Critical Slenderness Ratio.
What is the column buckling formula?
The column buckling formula used in this buckling load calculator is Euler’s formula for buckling when the column’s slenderness ratio exceeds its critical slenderness ratio. For cases where the slenderness ratio is lower, Johnson’s parabolic formula is used as an alternative.
Leonhard Euler was a Swiss mathematician who derived a formula that determines the load at which a column will buckle. The formula is relatively simple:
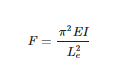
It is important to note that Euler’s formula is used in the buckling calculator when the column the slenderness ratio of the column member is greater than its critical slenderness ratio.
What is Johnson’s parabolic formula for column buckling?
J. B. Johnson developed the parabolic formula for column buckling for columns with a low slenderness ratio. Johnson’s Parabolic Formula is as follows:
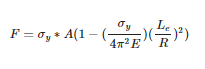
How is the effective length (K value) determined?
The effective length value (K) used in the SkyCiv Column Buckling Calculator is based on the recommended design value found in Table C-A-7.1 Approximate Values of Effective Length Factor, K of the ANSI/AISC 360-22 Specification for Structural Steel Buildings.
How to prevent buckling of columns?
If in the analysis stage of an engineering project, a column is found to be buckling then an engineer can try a couple of methods to ensure structural integrity. This first method includes increasing the cross-sectional dimensions of the column to enable improved column load capacity. Material changes are also possible, such as using higher strength/stiffness steel will again improve the columns load capacity. Finally if required the column can be braced, laterally supported, or reinforced to help it resist buckling. You can simulate these approaches in the SkyCiv buckling load calculator above.
Understanding column buckling vs critical buckling?
- Column Buckling is the general structural phenomenon used to describe when a column (vertical member) deflect sideways due to axial loads leading to a reduced compressive capacity in the column.
- Critical Buckling is a term used by engineers to design the specific point at which a column reaches it’s critical or maximum load a column can resist in it’s elastic range before buckling occurs.
Want to learn more about column buckling?
If you want to gain a deeper understanding of column buckling and understand the calculations provided in this buckling load calculator then SkyCiv has a detailed tutorial on Column Buckling to get you started.
Related Calculators
About SkyCiv
As well as our column buckling calculator SkyCiv offers a wide range of Cloud Structural Analysis and Design Software for engineers. As a constantly evolving tech company, we’re committed to innovating and challenging existing workflows to save engineers time in their work processes and designs.
Column Buckling Calculator FAQs
Your Questions Answered
PRICING
Access SkyCiv Quick Design
Intuitive Interface
Our easy to learn, powerful to use, intuitive interface allows you to quickly access all the features you need. Packed with smart features like the Pen tool, Repeat/Mirror, and Bulk Editing.Your Content Goes Here
Comprehensive Design Code Support
Our software supports a comprehensive array of steel, wood, and concrete design codes including AISC, EN, AISI, NDS, AS, and CSA.
API Technology
SkyCiv is a customised solution featuring seamless integrations, easy implementations, automated reports and a scalable design and architecture.
24/7 Customer Support
SkyCiv is a customised solution featuring seamless integrations, easy implementations, automated reports and a scalable design and architecture.
