How to calculate the ultimate load-carrying capacity of a single pile

Load-Carrying Capacity

---

Evaluating the ultimate load-carrying capacity of a single pile is one of the most important aspects of pile design, and can sometimes be complicated. This article will walk through the governing equations for single pile design as well as an example.

To easily understand the load transfer mechanism of a single pile, imagine a concrete pile of length L with diameter D, as shown in Figure 1.

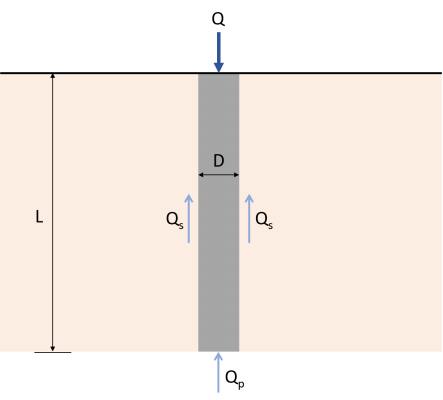
Figure 1: Load transfer Mechanism for piles

The load Q applied on the pile shall be transferred directly to the soil at the bottom of the pile. Part of this load will be resisted by the sides of the pile using something called “skin friction” developed along the shaft (Q_s), and the rest will be resisted by the soil that the pile is bearing on (Q_p).  Therefore, the ultimate load-carrying capacity (Qu) of a pile shall be given by the equation (1). There are multiple methods available to estimate the values of Q_p and Q_s.

\(    {Q}_{u} = {Q}_{p} + {Q}_{s}      \)    (1)

Q_u = Ultimate load-carrying capacity

Q_p = End-bearing load capacity

Q_s = Skin-frictional resistance

Want to try SkyCiv’s Foundation Design software? Our free tool allows users to perform load-carrying calculations without any download or installation!

Foundation Design Calculator

End-bearing Capacity, Q_p

---

Ultimate end-bearing capacity is theoretically the maximum load per unit area that can be supported by the soil in bearing, without failure. The following equation of Karl Von Terzaghi, the father of soil mechanics, is one of the first and most commonly used theory when evaluating the ultimate bearing capacity of foundations. Terzaghi’s equation for ultimate bearing capacity can be expressed as:

\(    {q}_{u} = (c × {N}_{c}) + (q × {N}_{q})  + (\frac{1}{2} × γ × B × {N}_{γ})   \)    (2)

q_u = Ultimate end-bearing capacity

c = Cohesion of soil

q = Effective soil pressure

γ = Soil unit weight

B = Cross-sectional depth or diameter

N_c, N_q, N_γ = Bearing factors

Since q_u is in terms of load per unit area or pressure, multiplying it by the cross-sectional area of the pile will result in the end-bearing load capacity (Q_p) of the pile. The resulting value of the last term of Equation 2 is negligible due to a relatively small pile width, hence,  it may be dropped from the equation. Thus, the ultimate end-bearing load capacity of the pile can be expressed as shown in equation (3). This modified version of Terzaghi’s equation is used in the SkyCiv Foundation module when designing piles.

\(    {Q}_{p} = {A}_{p} × [(c × {N}_{c}) + (q × {N}_{q}) ]   \)    (3)

A_p = Cross-sectional area of pile

Bearing factors N_c and N_q are non-dimensional, empirically derived, and are functions of the soil friction angle (Φ). Researchers have already completed the calculations required to find bearing factors. Table 1 summarizes the values of N_q according to Naval Facilities Engineering Command (NAVFAC DM 7.2, 1984). The value of N_c is approximately equal to 9 for piles under clayey soils.

Bearing Factor (Nq)
Friction Angle (Ø)	26	28	30	31	32	33	34	35	36	37	38	39	40
Driven Piles	10	15	21	24	29	35	42	50	62	77	86	120	145
Bored Piles	5	8	10	12	14	17	21	25	30	38	43	60	72

Table 1: N_q values from NAVFAC DM 7.2

Skin-frictional Resistance Capacity, Q_s

---

Skin-frictional resistance of piles is developed along the length of the pile. Generally, the frictional resistance of a pile is expressed as:

\(    {Q}_{s} = ∑ (p × ΔL ×  f)  \)    (4)

p = Perimeter of the pile

ΔL = Incremental pile length over which p and f are taken

f = Unit frictional resistance at any depth

Estimating the value of the unit frictional resistance (f) requires several important factors to consider, such as the nature of pile installation and soil classification. Equations (5) and (6) shows the computational method to find the unit frictional resistance of piles in sandy and clayey soils, respectively. Tables 2 and 3 present the recommended effective earth pressure coefficient (K) and the soil-pile frictional angle (δ’), according to NAVFAC DM7.2.

 For sandy soils:

\(    f = K × σ’× tan(δ’) \)    (5)

K = Effective earth pressure coefficient

σ’ = Effective vertical stress at the depth under consideration

δ’ = Soil-pile frictional angle

 For clayey soils:

\(    f =  α × c  \)    (6)

α = Empirical adhesion factor

Soil-Pile Frictional Angle (δ’)
Pile Type	δ’
Steel Pile	20º
Timber Pile	3/4 × Φ
Concrete Pile	3/4 × Φ

Table 2: Soil-Pile Frictional Angle Values (NAVFAC DM7.2, 1984)

Lateral Earth Pressure Coefficient (K)
Pile Type	Compression Pile	Tension Pile
Driven H-piles	0.5-1.0	0.3-0.5
Driven displacement piles (round, rectangular)	1.0-1.5	0.6-1.0
Driven displacement piles (tapered)	1.5-2.0	1.0-1.3
Driven jetted piles	0.4-0.9	0.3-0.6
Bored piles (<24″ Diameter)	0.7	0.4

Table 3: Lateral Earth Pressure Coefficient (K) Values (NAVFAC DM7.2, 1984)

Adhesion Factor (α)
c/pa	α
≤ 0.1	1.00
0.2	0.92
0.3	0.82
0.4	0.74
0.6	0.62
0.8	0.54
1.0	0.48
1.2	0.42
1.4	0.40
1.6	0.38
1.8	0.36
2.0	0.35
2.4	0.34
2.8	0.34

Note: p_a = atmospheric pressure ≈ 100 kN/m²

Table 4: Adhesion Factor Values (Terzaghi, Peck, and Mesri, 1996)

Example: Calculating the capacity of piles in sand

---

A 12-meter long concrete pile with a diameter of 500 mm is driven into multiple sand layers with no groundwater present. Find the ultimate load-carrying capacity (Q_u)  of the pile.

Details
Section
Diameter	500 mm
Length	12 m
Layer 1-Soil Properties
Thickness	5 m
Unit Weight	17.3 kN/m3
Friction Angle	30 Degrees
Cohesion	0 kPa
Groundwater Table	Not present
Layer 2-Soil Properties
Thickness	7 m
Unit Weight	16.9 kN/m3
Friction Angle	32 Degrees
Cohesion	0 kPa
Groundwater Table	Not present

Step 1: Compute the end-bearing load capacity (Q_p).

At the tip of the pile:

A_p = (π/4) × D² = (π/4) × 0.5²

A_p = 0.196 m²

c = 0 kPa

θ = 32º

N_q = 29 (From Table 1)

Effective soil pressure (q):

q =  (γ₁  × t₁) +  (γ₂  × t₂) =  (5 m × 17.3 kN/m³) +  (7 m × 16.9 kN/m³)

q = 204.8 kPa

Then use equation (3) for the end-bearing load capacity:

Q_p = A_p × [(c × N_c) + (q × N_q)]

   Q_p = 0.196 m² × ( 204.8 KPa × 29)

Q_p = 1,164.083 kN

Step 2:  Compute the skin-frictional resistance (Q_s).

Using equations (4) and (5), calculate the skin-frictional per soil layer.

Q_s = ∑ (p × ΔL ×  f)

p = π × D = π × 0.5 m

p = 1.571 m

Layer 1:

ΔL = 5 m

  f₁ = K × σ’₁× tan(δ’)

K = 1.25 (Table 3)

δ’ = 3/4 × 30º

δ’ = 22.50º

σ’₁ = γ₁  × (0.5 × t₁)  = 17.3 kN/m³ × (0.5 × 5 m)

σ’₁ = 43.25 kN/m²

f₁ = 1.25 × 43.25 kN/m² × tan(22.50º)

f₁ = 22.393 kN/m²

Q_s1 = p × ΔL ×  f₁ = 1.571 m ×5 m × 22.393 kN/m²

Q_s1 = 175.897 kN

Layer 2:

ΔL = 7 m

    f₂ = K × σ’₂× tan(δ’)

K = 1.25 (Table 3)

δ’ = 3/4× 32º

δ’ = 24º

σ’₂ = (γ₁  × t₁) + [γ₂  × (0.5 × t₂)]  = (17.3 kN/m³ × 5 m) + [16.9 kN/m³ ×(0.5 × 7 m)]

σ’₂ = 145.65 kN/m²

f₂ = 1.25 × 145.65 kN/m² × tan(24º)

f₂ = 81.059 kN/m²

Q_s2 = p × ΔL ×  f₂ = 1.571 m ×7 m × 81.059 kN/m²

Q_s2 = 891.406 kN

Total skin-frictional resistance:

Q_s = Q_s1+ Q_s2 = 175.897 kN + 891.406 kN

Q_s = 1,067.303 kN

Step 3:  Compute for the ultimate load-carrying capacity (Q_u).

Q_u = Q_p+ Q_s = 1,164.083 kN + 1,067.303 kN

Q_u = 2,231.386 kN

Example 2: Calculating the capacity of piles in clay

---

Consider a 406 mm diameter concrete pile with a length of 30m embedded in layered, saturated clay. Find the ultimate load-carrying capacity (Q_u)  of the pile.

Details
Section
Diameter	406 mm
Length	30 m
Layer 1-Soil Properties
Thickness	10 m
Unit Weight	8 kN/m3
Friction Angle	0º
Cohesion	30 kPa
Groundwater Table	5 m
Layer 2-Soil Properties
Thickness	10 m
Unit Weight	19.6 kN/m3
Friction Angle	0º
Cohesion	0 kPa
Groundwater Table	Fully submerged

Step 1: Compute the end-bearing load capacity (Q_p).

At the tip of the pile:

A_p = (π/4) × D²= (π/4) × 0.406²

A_p = 0.129 m²

c = 100 kPa

N_c = 9 (Typical value for clay)

Q_p = (c × N_c) × A_p = (100 kPa × 9) × 0.129 m²

Q_p = 116.1 kN

Step 2: Compute the skin-frictional resistance (Q_s).

Using equations (4) and (6), calculate the skin-frictional per soil layer.

    Q_s  = ∑ (p × ΔL ×  f)

p = π × D = π × 0.406 m

p = 1.275 m

Layer 1:

ΔL = 10 m

α₁ = 0.82 (Table 4)

c₁ = 30 kPa

   f₁=  α₁ × c₁  = 0.82 × 30 kPa

f₁ = 24.6 kN/m²

Q_s1  = p × ΔL ×  f₁ = 1.275 m × 10 m × 24.6 kN/m²

Q_s1 = 313.65 kN/m²

Layer 2:

ΔL = 20 m

α₂= 0.48 (Table 4)

c₂ = 100 kPa

f₂  =  α₂ × c₂  = 0.48 × 100 kPa

f₂ = 48 kN/m²

Q_s2  = p × ΔL ×  f₂  = 1.275 m × 20 m × 48 kN/m²

Q_s2 = 1,224 kN/m²

Total skin-frictional resistance:

Q_s = Q_s1+ Q_s2 = 313.65 kN + 1224 kN

Q_s = 1,537.65 kN

Step 3:  Compute for the ultimate load-carrying capacity (Q_u).

Q_u = Q_p+ Q_s = 116.1 kN + 1537.65 kN

Q_u = 1,653.75 kN

Want to try SkyCiv’s Foundation Design software? Our free tool allows users to perform load-carrying calculations without any download or installation!

Foundation Design Calculator

References:

• Das, B.M. (2007). Principles of Foundation Engineering (7th Edition). Global Engineering
• Rajapakse, R. (2016). Pile Design and Construction Rule of Thumb (2nd Edition). Elsevier Inc.
• Tomlinson, M.J. (2004). Pile Design and Construction Practice (4th Edition). E & FN Spon.