The Fundamentals of the Centroid
It is important to note that on a cross-section, whose area is uniform throughout, the centroid can be found by taking the summation of moments with respect to an axis arbitrarily set, but is usually set at the top or bottom fiber. Check out our previous article on how to find centroid of a beam section and SkyCiv Free Centroid Calculator.
Fundamentally, the centroid can be obtained by taking the summation of moments over the summation of the area. Which is expressed in this way.
[math]
\bar{x}=\frac{1}{A}\int xf\left ( x \right )dx
[math]

Summary of Centroid Equations
In the equation above, f(x) is the function and x is the moment arm. To better illustrate this, we will derive the y centroid of an arbitrary triangle with its base coincident to the x-axis. In this situation, the shape of the triangle, whether be it equilateral, isosceles or scalene is irrelevant as everything is relative to only the x-axis. Note the shape is irrelevant if the triangle’s base is coincident or parallel with respect to the axis. This will not be the case when solving for the x centroid. Instead, you can imagine it as getting the centroid of two right triangles with respect to the y-axis. For the sake of convenience, let us imagine an isosceles triangle similar to the reference table below. Finding the relationship between b and h will yield the following relationship.
[math]
\frac{-y}{x}=\frac{-h}{b}
[math]
Note that the slope is negative as we are imagining the triangle to be upright. If we imagine the triangle to be inverted, the slope would be positive. Regardless, the relationship remains the same. As x = f(y), the relationship above can be rewritten like the following.
[math]
x=f\left ( y \right )=\frac{b}{h}y
[math]
We can now solve for centroid. Adjusting the first equation above, we get the following.
[math]
\bar{y}=\frac{1}{A}\int yf\left ( y \right )dy
[math]
Plugging additional values and substituting the relationship above will yield the following equation.
[math]
\bar{y}=\frac{2}{bh}\int_{0}^{h} \frac{b}{h}y^{2}dy
[math]
Simplifying,
[math]
\bar{y}=\frac{2}{h^{2}}\left [ \frac{y^{3}}{3} \right ]_{0}^{h}
[math]
[math]
\bar{y}=\frac{2}{h^{2}}\left [ \frac{h^{3}}{3}-0 \right ]
[math]
[math]
\bar{y}=\frac{2}{3}h
[math]
Note that this solution is taken from the top. The centroid taken from the bottom must then be equal to 1/3 of h.
Formula for centroids of common shapes and beam sections
Below is a list of a variety of beam section shapes and the distance to the centroids of the section. The equations show how to find the centroid of a particular section from the base or the furthest left point of the section. For SkyCiv Student and Structural subscriptions, this reference can also be downloaded as a PDF Reference to take with you wherever you go. Centroids of a beam section are extremely important as they locate the Neutral Axis and are one of the earliest steps required when analyzing a beam section.
SkyCiv also offers a comprehensive Summary of Sections Table which contains all the equations and formulas relating to beam sections (moment of inertia, area etc…).
The equation for various centroids are listed below:
| REFERENCE | Cy (Distance from bottom) |
Cx (Distance from furthest left point) |
Centroid of Rectangle or Rectangular Sections |
||
|---|---|---|
 |
[math] \dfrac{h}{2} [math] |
[math] \dfrac{b}{2} [math] |
Centroid of a Hollow Rectangular Section |
||
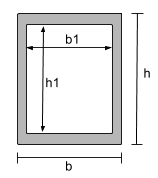 |
[math] \dfrac{b}{2} [math] |
[math] \dfrac{h}{2} [math] |
Centroid of a Circle or Circular Section |
||
 |
[math] \dfrac{D}{2} [math] |
[math] \dfrac{D}{2} [math] |
Centroid Equation of a Hollow Circular Section |
||
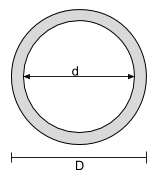 |
[math] \dfrac{D}{2} [math] |
[math] \dfrac{D}{2} [math] |
Centroid of an Isosceles Triangle |
||
 |
[math] \dfrac{h}{3} [math] |
[math] \dfrac{b}{2} [math] |
Centroid of an I Beam |
||
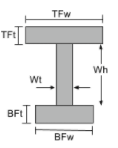 |
[math] \frac{TFw\times TFt\times \left ( BFt + Wh + \frac{TFt}{2} \right )}{TFw\times TFt + Wt\times Wh + BFw\times BFt} + [math] [math] \frac{Wt\times Wh\times \left ( BFt + \frac{Wh}{2} \right )}{TFw\times TFt + Wt\times Wh + BFw\times BFt} + [math] [math] \frac{BFw\times BFt\times \left ( \frac{BFt}{2} \right )}{TFw\times TFt + Wt\times Wh + BFw\times BFt} [math] |
[math] TFw > BFw, \frac{TFw}{2}[math] [math] BFw > TFw, \frac{BFw}{2} [math] |
Centroid of a T-Section |
||
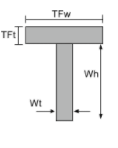 |
[math] \frac{Wt\times Wh\times \left ( \frac{Wh}{2} \right )}{TFw\times TFt + Wt\times Wh } + [math] [math] \frac{TFw\times TFt\times \left ( Wh + \frac{TFt}{2} \right ) }{TFw\times TFt + Wt\times Wh } [math] |
[math] \frac{TFw}{2} [math] |
Centroid of an C-Section |
||
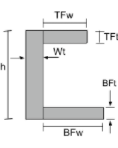 |
[math] \frac{TFw\times TFt\times \left ( h – \frac{TFt}{2} \right )}{TFw\times TFt + Wt\times Wh + BFw\times BFt} + [math] [math] \frac{Wt\times h\times \left ( \frac{h}{2} \right )}{TFw\times TFt + Wt\times Wh + BFw\times BFt} + [math] [math] \frac{BFw\times BFt\times \left ( \frac{BFt}{2} \right )}{TFw\times TFt + Wt\times Wh + BFw\times BFt} [math] |
[math] \frac{TFt\times TFw\times \left ( Wt + \frac{TFw}{2} \right )}{TFt\times TFw + h\times Wt + BFt\times BFw} + [math] [math] \frac{h\times Wt\times \left ( \frac{Wt}{2} \right )}{TFt\times TFw + h\times Wt + BFt\times BFw} + [math] [math] \frac{BFt\times BFw\times \left ( Wt + \frac{BFw}{2} \right )}{TFt\times TFw + h\times Wt + BFt\times BFw} [math] |
Centroid of an Angles |
||
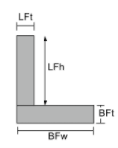 |
[math] \frac{LFt\times LFh\times \left ( BFt + \frac{LFh}{2} \right ) }{LFt\times LFh + BFw\times BFt} + [math] [math] \frac{BFw\times BFt\times \left ( \frac{BFt}{2} \right )}{LFt\times LFh + BFw\times BFt} [math] |
[math] \frac{LFh\times LFt\times \left ( \frac{LFt}{2} \right )}{LFh\times LFt + BFt\times BFw} + [math] [math] \frac{BFt\times BFw\times \left ( \frac{BFw}{2} \right )}{LFh\times LFt + BFt\times BFw} [math] |
Automatic Equations for Centroid of Beam
Check out our Free Centroid Calculator, a simplified version of SkyCiv Section Builder, to calculate centroid of beam automatically with no need for hand calculations. Or sign up today to get started!


