SkyCiv released a free wind load calculator that has several code references including the ASCE 7-10 wind load procedure. In this section, we are going to demonstrate how to calculate the wind loads, by using an S3D warehouse model below:
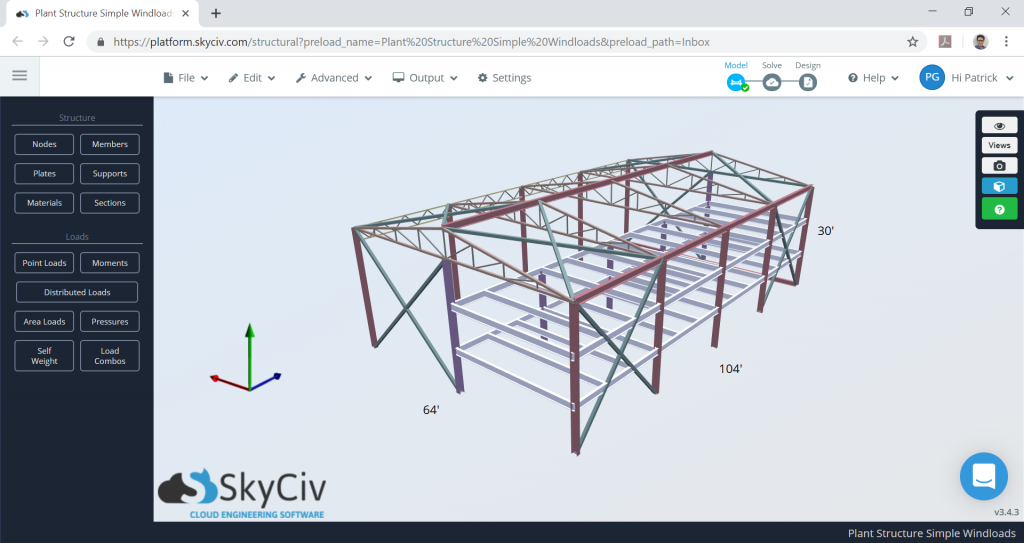
Figure 1. Warehouse model in SkyCiv S3D as an example.
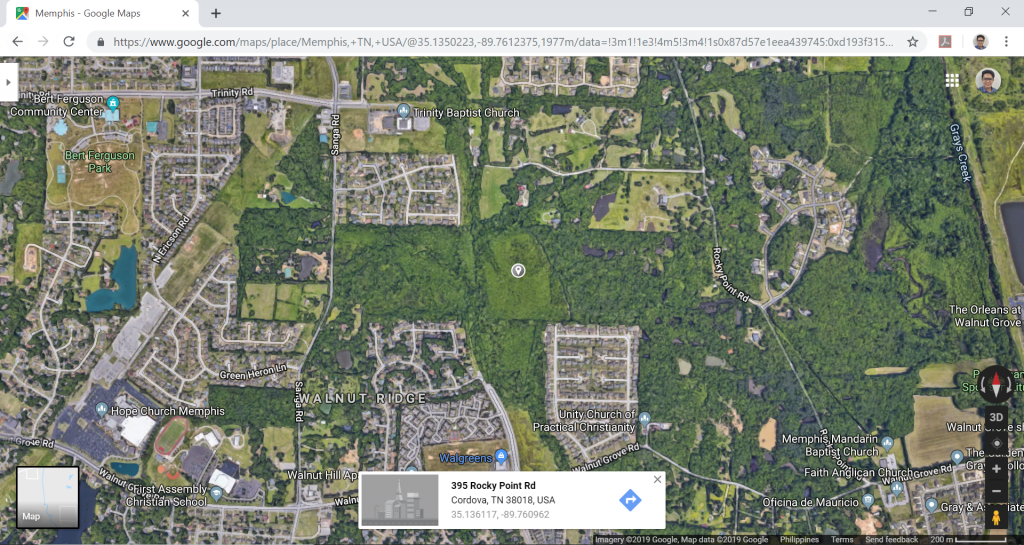
Figure 2. Site location (from Google Maps).
Table 1. Building data needed for our wind calculation.
| Location | Cordova, Memphis, Tennessee |
| Occupancy | Miscellaneous – Plant Structure |
| Terrain | Flat farmland |
| Dimensions | 64 ft × 104 ft in plan Eave height of 30 ft Apex height at elev. 36 ft Roof slope 3:16 (10.62°) With opening |
| Cladding | Purlins spaced at 2ft Wall studs spaced at 2ft |
In our wind load example, design wind pressures for a large, three-story plant structure will be determined. Fig. 1 shows the dimensions and framing of the building. The building data are shown in Table 1.
Although there are a number of software that have wind load calculation already integrated into their design and analysis, only a few provide a detailed computation of this specific type of load. Users would need to conduct manual calculations of this procedure in order to verify if the results are the same as those obtained from the software.
Wind Load Calculation Formulas
Below are the formulas in determining the design wind pressure.
For enclosed and partially enclosed buildings:
\(p = qG{C}_{p} -{q}_{i}({GC}_{pi})\) (1)
For open buildings:
\(p = q{G}_{f}{C}_{p} -{q}({GC}_{pi})\) (2)
Where:
\(G\) = gust effect factor
\({C}_{p}\) = external pressure coefficient
\(({GC}_{pi})\)= internal pressure coefficient
\(q\) = velocity pressure, in psf, given by the formula:
\(q = 0.00256{K}_{z}{K}_{zt}{K}_{d}V^2\) (3)
\(q\) = \({q}_{h}\) for leeward walls, side walls, and roofs,evaluated at roof mean height, \(h\)
\(q\) = \({q}_{z}\) for windward walls, evaluated at height, \(z\)
\({q}_{i}\) = \({q}_{h}\) for negative internal pressure, \((-{GC}_{pi})\) evaluation and \({q}_{z}\) for positive internal pressure evaluation \((+{GC}_{pi})\) of partially enclosed buildings but can be taken as \({q}_{h}\) for conservative value.
\({K}_{z}\) = velocity pressure coefficient
\({K}_{zt}\)= topographic factor
\({K}_{d}\)= wind directionality factor
\(V\) = basic wind speed in mph
We will dive deep into the details of each parameter below. Moreover, we will be using the Directional Procedure (Chapter 30 of ASCE 7-10) in solving the design wind pressures.
Parameter explanations
Risk Category
The first thing to do in determining the design wind pressures is to classify the risk category of the structure which is based on the use or occupancy of the structure. For this example, since this is a plant structure, the structure is classified as Risk Category IV. See Table 1.5-1 of ASCE 7-10 for more information about risk categories classification.
Basic Wind Speed, \(V\)
The ASCE 7-10 provides a wind map where the corresponding basic wind speed of a location can be obtained from Figures 26.5-1A to 1C. The Occupancy Category is defined and classified in the International Building Code.
When viewing the wind maps, take the highest category number of the defined Risk or Occupancy category. In most cases, including this example, they are the same. From Figure 26.5-1B, Cordova, Memphis, Tennessee is somehow near where the red dot on Figure 3 below, and from there, the basic wind speed, \(V\), is 120 mph. Take note that for other locations, you would need to interpolate the basic wind speed value between wind contours.
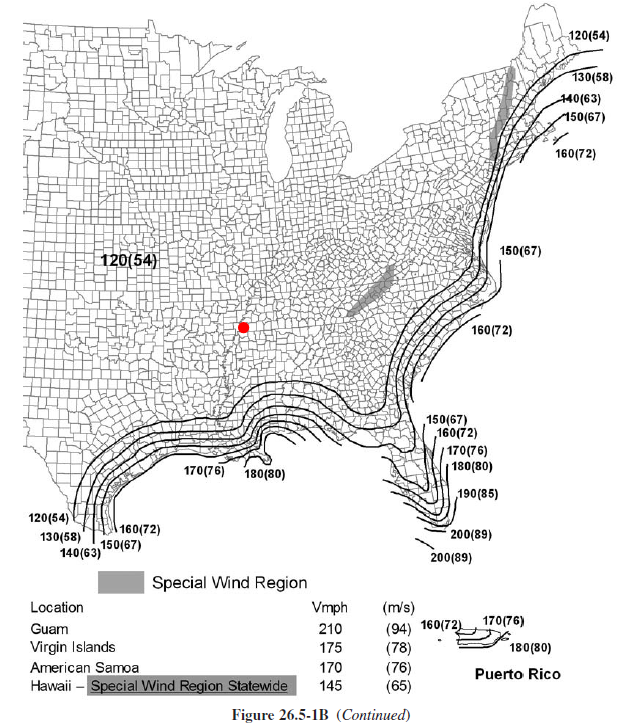
Figure 3. Basic wind speed map from ASCE 7-10.
SkyCiv now automates the wind speed calculations with a few parameters. Try our SkyCiv Free Wind Tool
Exposure Category
See Section 26.7 for details of the procedure in determining the exposure category.
Depending on the wind direction selected, the exposure of the structure shall be determined from the upwind 45° sector. The exposure to be adopted should be the one that will yield the highest wind load from the said direction.
The description of each exposure classification is detailed in Section 26.7.2 and 26.7.3. To better illustrate each case, examples of each category are shown in the table below.
Table 2. Examples of areas classified according to exposure category (Chapter C26).
| Exposure | Example |
|---|---|
| Exposure B |
|
| Exposure C |
|
| Exposure D |
|
For our example, since the location of the structure is in farmland in Cordova, Memphis, Tennessee, without any buildings taller than 30 ft, therefore the area is classified as Exposure C. A helpful tool in determining the exposure category is to view your potential site through a satellite image (Google Maps for example).
Wind Directionality Factor, \({K}_{d}\)
The wind directionality factors, \({K}_{d}\), for our structure are both equal to 0.85 since the building is the main wind force resisting system and also has components and cladding attached to the structure. This is shown in Table 26.6-1 of ASCE 7-10 as shown below in Figure 4.
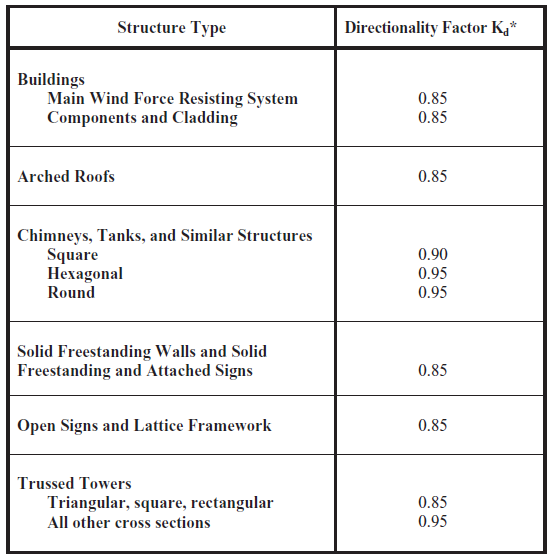
Figure 4. Wind directionality factor based on structure type (Table 26.6-1).
Topographic Factor, \({K}_{zt}\)
Since the location of the structure is in flat farmland, we can assume that the topographic factor, \({K}_{zt}\), is 1.0. Otherwise, the factor can be solved using Figure 26.8-1. To determine if further calculations of the topographic factor are required, see Section 26.8.1, if your site does not meet all of the conditions listed, then the topographic factor can be taken as 1.0.
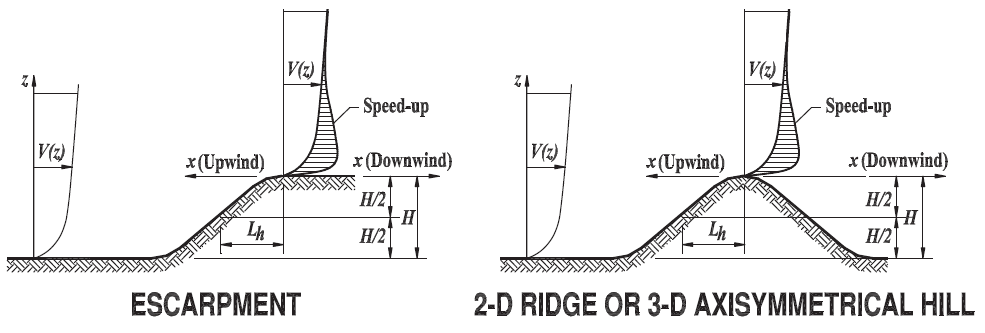
Figure 5. Parameters needed in calculation topographic factor, \({K}_{zt}\) (Table 26.8-1).
Note: Topography factors can automatically be calculated using SkyCiv Wind Design Software
Velocity Pressure Coefficient, \({K}_{z}\)
The velocity pressure coefficient, \({K}_{z}\), can be calculated using Table 27.3-1. This parameter depends on the height above ground level of the point where the wind pressure is considered, and the exposure category. Moreover, the values shown in the table is based on the following formula:
For 15ft < \({z}\) < \({z}_{g}\): \({K}_{z} = 2.01(z/{z}_{g})^{2/α}\) (4)
For \({z}\) < 15ft: \({K}_{z} = 2.01(15/{z}_{g})^{2/α}\) (5)
Where:
Table 3. Values of and \({z}_{g}\) from table 26.9-1 of ASCE 7-10.
| Exposure | α | \({z}_{g}\)(ft) |
| B | 7 | 1200 |
| C | 9.5 | 900 |
| D | 11.5 | 700 |
Usually, velocity pressure coefficients at the mean roof height, \({K}_{h}\), and at each floor level, \({K}_{zi}\), are the values we would need in order to solve for the design wind pressures. For this example, since the wind pressure on the windward side is parabolic in nature, we can simplify this load by assuming that uniform pressure is applied on walls between floor levels.
The plant structure has three (3) floors, so we will divide the windward pressure into these levels. Moreover, since the roof is a gable-style roof, the roof mean height can be taken as the average of roof eaves and apex elevation, which is 33 ft.
Table 4. Calculated values of velocity pressure coefficient for each elevation height.
| Elevation (ft) | \({K}_{z}\) |
| 10 | 0.85 |
| 20 | 0.90 |
| 30 | 0.98 |
| 33 | 1.00 \({K}_{zh}\) |
Velocity Pressure
From Equation (3), we can solve for the velocity pressure, \(q\) in PSF, at each elevation being considered.
Table 5. Calculated values of velocity pressure at each elevation height.
| Elevation (ft) | \({K}_{z}\) | \(q\)(psf) | Remarks |
| 10 | 0.85 | 26.63 | 1st floor |
| 20 | 0.90 | 28.20 | 2nd floor |
| 30 | 0.98 | 30.71 | Roof eave |
| 33 | 1.00 | 31.33 | Roof mean height, \({q}_{h}\) |
Calculation Methodology
Gust Effect Factor, G
The gust effect factor, \(G\), is set to 0.85 as the structure is assumed rigid (Section 26.9.1 of ASCE 7-10).
Enclosure Classification and Internal Pressure Coefficient
The plant structure is assumed to have openings that satisfy the definition of a partially enclosed building in Section 26.2 of ASCE 7-10. Thus, the internal pressure coefficient, \(({GC}_{pi})\), shall be +0.55 and -0.55 based on Table 26.11-1 of ASCE 7-10.
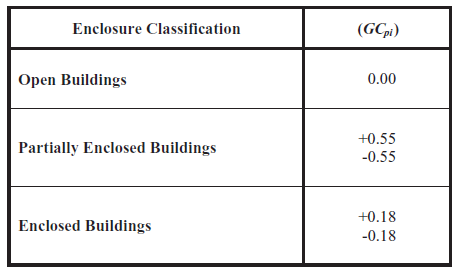
Figure 6. Internal Pressure Coefficient, \(({GC}_{pi})\) (Table 26.11-10).
External Pressure Coefficient, \({C}_{p}\)
For enclosed and partially enclosed buildings, the External Pressure Coefficient, \({C}_{p}\), is calculated using the information provided in Figure 27.4-1 through Figure 27.4-3. For a partially enclosed building with a gable roof, use Figure 27.4-1.
External Pressure Coefficients for the walls and roof are calculated separately using the building parameters L, B, and h, which are defined in Note 7 of Figure 27.4-1.
Thus, we need to calculate the L/B and h/L:
Roof mean height, h = 33′
Building length, L = 64′
Building width, B = 104′
L/B = 0.615
h/L = 0.516
h/B = 0.317
From these values, we can obtain the external pressure coefficients, \({C}_{p}\), for each surface using table 27.4-1. Take note that we can use linear interpolation when roof angle, θ, L/B, and h/L values are in between those that are in the table. For our example, the external pressure coefficients of each surface are shown in Tables 6 to 8.
Table 6. Calculated external pressure coefficients for wall surfaces.
| Surface | \({C}_{p}\) |
| Windward wall | 0.8 |
| Leeward wall | -0.5 |
| Side wall | -0.7 |
Table 7. Calculated external pressure coefficients for roof surfaces (wind load along L).
| External pressure coefficients for roof \({C}_{p}\) (along L) | ||||||
| h/L | Windward | Leeward | ||||
| 10° | 10.62° | 15° | 10° | 10.62° | 15° | |
| 0.5 | -0.9 -0.18 |
-0.88 -0.18 |
-0.7 -0.18 |
-0.50 | -0.50 | -0.50 |
| 0.516 | -0.91 -0.18 |
-0.89 -0.18 |
-0.71 -0.18 |
-0.51 | -0.51 | -0.50 |
| 1.0 | -1.3 -0.18 |
-1.26 -0.18 |
-1.0 -0.18 |
-0.70 | -0.69 | -0.60 |
Table 8. Calculated external pressure coefficients for roof surfaces (wind load along B).
| External pressure coefficients for roof \({C}_{p}\) (along B) | ||
| h/B | Location | \({C}_{p}\) |
| 0.317 | 0 to h | -0.9 -0.18 |
| h/2 to h | -0.9 -0.18 |
|
| h to 2h | -0.5 -0.18 |
|
| >2h | -0.3 -0.18 |
|
External pressure coefficient with two values as shown in Tables 7 and 8 shall be checked for both cases.
Design Wind Pressures
Main Wind Frame Resisting System
Using Equation (1), the design wind pressures can be calculated. Results of our calculations are shown on Tables 8 and 9 below. Take note that there will be four cases acting on the structure as we will consider pressures solved using \((+{GC}_{pi})\) and \((-{GC}_{pi})\) , and the \(+{C}_{p}\) and \(-{C}_{p}\) for roof.
Table 9. Design wind pressure for wall surfaces.
| Design Pressure, \(p\), for Walls |
|||||||
| Floor elevation | \({q}_{z}\), psf | Windward | Leeward | Side wall | |||
| \((+{GC}_{pi})\) | \((-{GC}_{pi})\) | \((+{GC}_{pi})\) | \((-{GC}_{pi})\) | \((+{GC}_{pi})\) | \((-{GC}_{pi})\) | ||
| 10 | 26.63 | 0.88 (0.88) | 35.35 (35.35) | -30.55 (-30.55) |
3.92 (3.92) |
-35.88 (-35.88) |
-1.41 (-1.41) |
| 20 | 28.20 | 1.94 (1.94) | 36.41 (36.41) | ||||
| 30 | 30.71 | 3.65 (3.65) | 38.12 (38.12) | ||||
| 33 | 31.33 | 4.07 (4.07) | 38.54 (38.54) | ||||
(SkyCiv Wind Load results)
Table 10. Design wind pressure for roof surfaces.
| Design Roof Pressure, psf (along L) | Design Roof Pressure, psf (along B) | ||||
| Surface | \((+{GC}_{pi})\) | \((-{GC}_{pi})\) | Location (from windward edge) |
\((+{GC}_{pi})\) | \((-{GC}_{pi})\) |
| Windward | -40.87 (-40.87) | -6.41 (-6.40) | 0 to h/2 | -41.20(-41.20) | 12.44(12.44) |
| -22.03 (-22.03) | 12.44 (12.44) | h/2 to h | -41.20(-41.20) | ||
| Leeward | -30.71 (-30.71) | 3.76 (3.83) | h to 2h | -30.55(-30.55) | |
| >2h | -25.22(-25.22) | ||||
(SkyCiv Wind Load results)
To apply these pressures to the structure, we will consider a single frame on the structure. Sample of applying case 1 and 2 (for both \(({GC}_{pi})\)) are shown in Figures 7 and 8. The wind direction shown in the aforementioned figures is along the length, L, of the building.
Take note that a positive sign means that the pressure is acting towards the surface while a negative sign is away from the surface. Bay length is 26 feet.
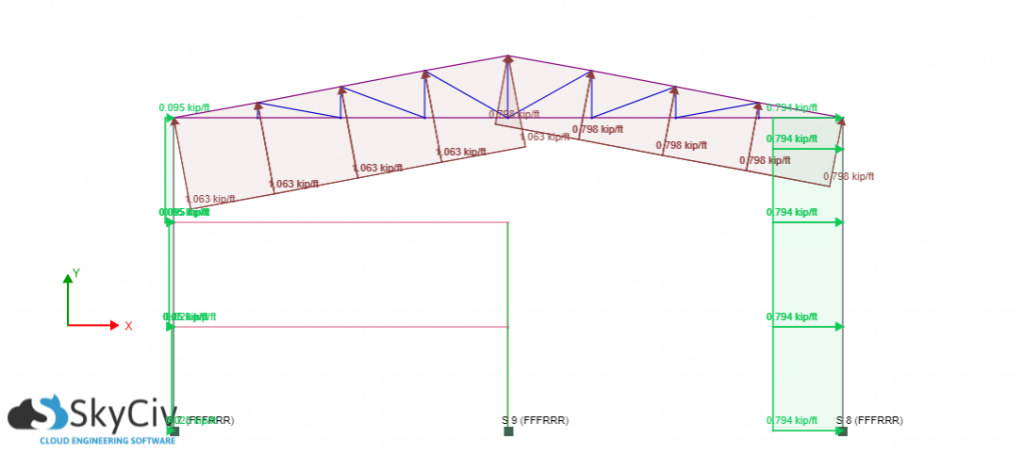
Figure 7. Design wind pressure applied on one frame – \((+{GC}_{pi})\) and absolute max roof pressure case.
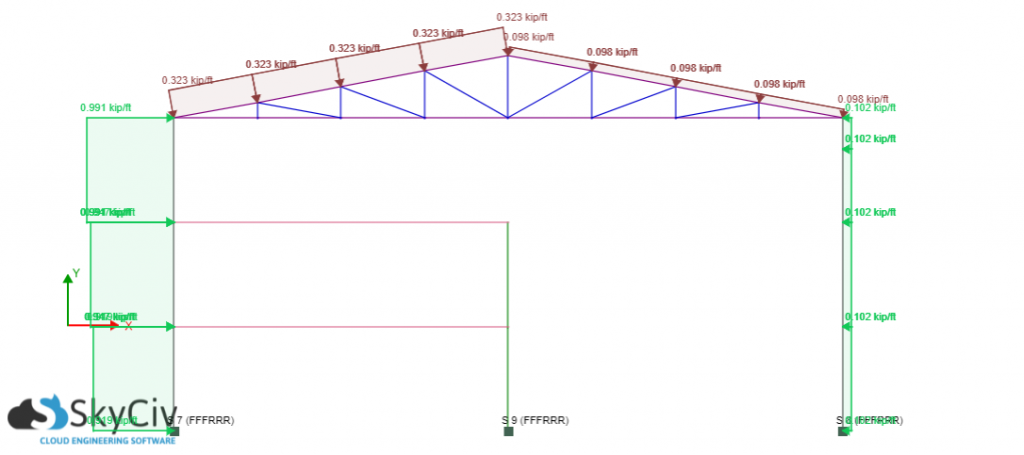
Figure 8. Design wind pressure applied on one frame – \((-{GC}_{pi})\) and absolute max roof pressure case.
SkyCiv simplifies this procedure by just defining parameters. Try our SkyCiv Free Wind Tool
Components and Cladding (C&C)
Components and claddings are defined in Chapter C26 as: “Components receive wind loads directly or from cladding and transfer the load to the MWFRS” while “cladding receives wind loads directly.” Examples of components include “fasteners, purlins, studs, roof decking, and roof trusses” and for cladding are “wall coverings, curtain walls, roof coverings, exterior windows, etc.”
From Chapter 30, design pressure for components and cladding shall be computed using the equation (30.4-1), shown below:
\(p = {q}_{h}[({GC}_{p})-({GC}_{pi})]\) (6)
Where:
\({q}_{h}\): velocity pressure evaluated at mean roof height, h (31.33 psf)
\(({GC}_{pi}\)): internal pressure coefficient
\(({GC}_{p}\)): external pressure coefficient
For this example, \(({GC}_{p}\)) will be found using Figure 30.4-1 for Zone 4 and 5 (the walls), and Figure 30.4-2B for Zone 1-3 (the roof). In our case, the correct figure used depends on the roof slope, θ, which is 7°< θ ≤ 27°. \(({GC}_{p}\)) can be determined for a multitude of roof types depicted in Figure 30.4-1 through Figure 30.4-7 and Figure 27.4-3 in Chapter 30 and Chapter 27, respectively.
We shall only calculate the design wind pressures for purlins and wall studs. Zones for components and cladding pressures are shown in Figure 9.
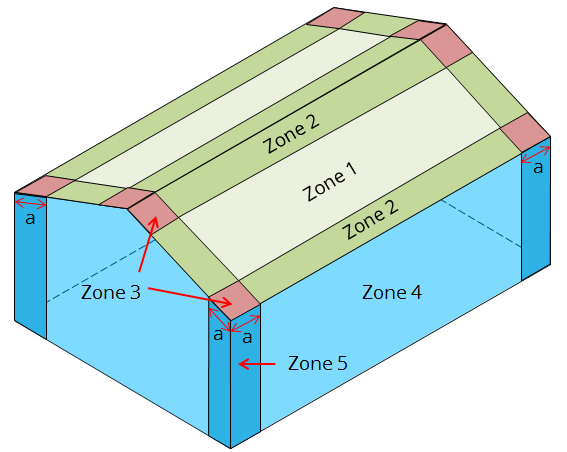
Figure 9. Location of calculated C&C pressures.
The distance a from the edges can be calculated as the minimum of 10% of least horizontal dimension or 0.4h but not less than either 4% of least horizontal dimension or 3 ft.
a : 10% of 64ft = 6.4 ft > 3ft
0.4(33ft) = 13.2 ft 4% of 64ft = 2.56 ft
a = 6.4 ft
Wall Studs (C&C Wall Pressure)
Based on Figure 30.4-1, the \(({GC}_{p}\)) can be calculated for zones 4 and 5 based on the effective wind area. Take note that the definition of effective wind area in Chapter C26states that: “To better approximate the actual load distribution in such cases, the width of the effective wind area used to evaluate \(({GC}_{p}\)) need not be taken as less than one-third the length of the area.” Hence, the effective wind area should be the maximum of:
Effective wind area = 10ft*(2ft) or 10ft*(10/3 ft) = 20 sq.ft. or 33.3 sq ft.
Effective wind area = 33.3 sq ft.
The positive and negative \(({GC}_{p}\)) for walls can be approximated using the graph shown below, as part of Figure 30.4-1:
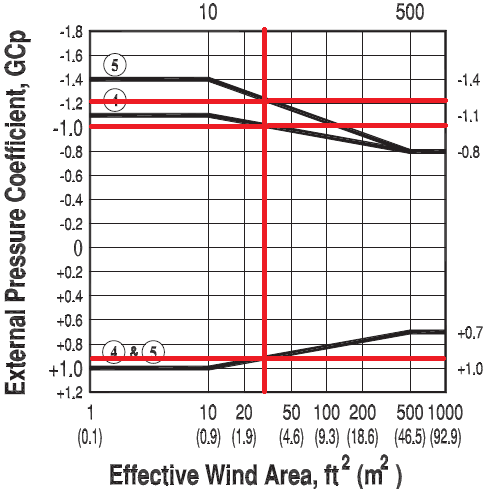
Figure 10. Approximated \(({GC}_{p}\)) values from Figure 30.4-1 of ASCE 7-10.
Table 11. Calculated C&C pressures for wall stud.
| Zone | \(+({GC}_{p}\)) | \(-({GC}_{p}\)) | C&C Pressures, psf | |
| \(+({GC}_{p}\)) | \(-({GC}_{p}\)) | |||
| 4 | 0.90 | -1.0 | 10.97 45.43 |
-48.56 -14.10 |
| 5 | 0.90 | -1.2 | 10.97 45.43 |
-54.83 -20.36 |
Purlins (C&C Roof Pressure)
From 30.4-2B, the effective wind pressures for Zones 1, 2, and 3 can be determined. Since trusses are spaced at 26ft, hence, this will be the length of purlins. The effective wind area should be the maximum of:
Effective wind area = 26ft*(2ft) or 26ft*(26/3 ft) = 52 ft2 or 225.33 sq.ft.
Effective wind area = 225.33 sq.ft.
The positive and negative \(({GC}_{p}\)) for the roof can be approximated using the graph shown below, as part of Figure 30.4-2B:
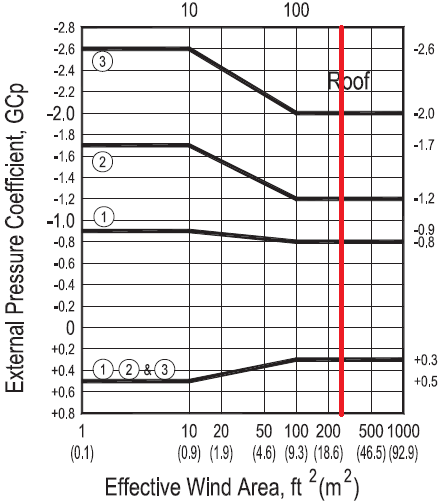
Figure 11. \(({GC}_{p}\)) values from Figure 30.4-2B.
Table 12. Calculated C&C pressures for purlins.
| Zone | +(GCp) | -(GCp) | C&C Pressures, psf | |
| +(GCpi) | -(GCpi) | |||
| 1 | 0.30 | -0.80 | -7.83 26.63 |
-42.30 -7.83 |
| 2 | 0.30 | -1.2 | -7.83 26.63 |
-54.83 -20.36 |
| 3 | 0.30 | -2.0 | -7.83 26.63 |
-79.89 -45.43 |
These calculations can be all be performed using SkyCiv’s Wind Load Software for ASCE 7-10, 7-16, EN 1991, NBBC 2015, and AS 1170. Users can enter in a site location to get wind speeds and topography factors, enter in building parameters and generate the wind pressures. With a Professional Account, users can auto-apply this to a structural model and run structural analysis all in one software.
Otherwise, try our SkyCiv Free Wind Tool or book a FREE DEMO so we can assist you with your specific needs
Structural Engineer, Product Development
MS Civil Engineering
References:
- Mehta, K. C., & Coulbourne, W. L. (2013, June). Wind Loads: Guide to the Wind Load Provisions of ASCE 7-10. American Society of Civil Engineers.
- Minimum Design Loads for Buildings and Other Structures. (2013). ASCE/SEI 7-10. American Society of Civil Engineers.



