Table of Contents
- Overview – What is the Moment of Inertia
- Example – How to Calculate the Moment of Inertia
- Formula and Equations
- Calculators
- Practice Questions
Overview – What is the Moment of Inertia?
In the context of structural engineering, the Moment of Inertia is a section property used to determine a structural element’s ability to resist bending and torsional forces. It’s usually a pretty good indicator of the sections stiffness and strength under load. A higher moment of inertia means the structure is better equipped to resist bending and deflection, making it an essential factor in designing beams, columns, and other load-bearing components. As a side note: Sometimes this is incorrectly defined as second moment of inertia, however this is incorrect. The other names for Moment of Inertia are: area moment of inertia, or second moment of area.
Example – How to Calculate Moment of Inertia of a Beam Section
Before we find the moment of inertia of a beam section (also known as second moment of area of a beam section), its centroid (or center of mass) must be known. For instance, if the moment of inertia of the section about its horizontal (XX) axis was required then the vertical (y) centroid would be needed first (Please view our tutorials on calculating the centroid of a beam section and calculating the statical/first moment of area).
Before we start, if you were looking for our Free Moment of Inertia Calculator please click the link to learn more. This will calculate the centroid, moment of inertia, and other results and even show you the step-by-step calculations! But for now, let’s look at a step-by-step guide and example of how to calculate the moment of inertia:
Step 1: Segment the beam section into parts
When calculating the area moment of inertia, we must calculate the moment of inertia of smaller segments. Try to break them into simple rectangular sections. For instance, consider the I-beam section below, which was also featured in our centroid tutorial. We have chosen to split this section into 3 rectangular segments:
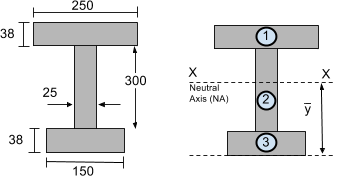
Step 2: Calculate the Neutral Axis (NA)
The Neutral Axis (NA) or the horizontal XX axis is located at the centroid or center of mass. In our centroid tutorial, the centroid of this section was previously found to be 216.29 mm from the bottom of the section – this is covered in our how to find the centroid of a shape tutorial. These can also simply be calculated from our centroid calculator or from common centroid equations.
Calculating the centroid, or Neutral Axis, is essential in how to calculate moment of inertia of a beam, as this is the axis at which the moment of inertia acts.
Step 3: Calculate Moment of Inertia
To calculate the total moment of inertia of the section we need to use the “Parallel Axis Theorem”:

Since we have split it into three rectangular parts, we must calculate the moment of inertia of each of these sections. It is widely known that the moment of inertia equation of a rectangle about its centroid axis is simply:
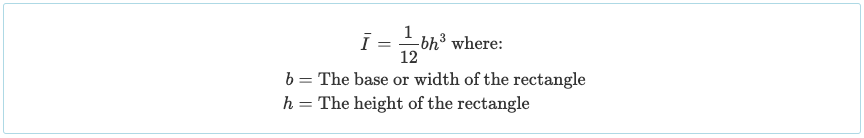
The moment of inertia of other shapes is often stated in the front/back of textbooks or from this guide of the moment of inertia shapes. However the rectangular shape is very common for beam sections, so it is probably worth memorizing.
Now we have all the information we need to use the “Parallel Axis Theorem” and find the total moment of inertia of the I-beam section. In our moment of inertia example:

So there you have our guide on calculating the area of moment for beam sections. This result is critical in structural engineering and is an important factor in the deflection of a beam. We hope you enjoyed the tutorial and look forward to any comments you have. For more information, visit our tutorial on Moment of Inertia Formula and Equations.
Formula and Equations
Each section type (rectangular, I Beam, Circular) has its own formula for quick calculation. These are simplified equations that let engineers quickly and easily calculate this important property.
The equations are a simplified expression of the above steps. For example, the formula for the moment of inertia of an Hollow Rectangle is basically the MOI of the larger section – the smaller (internal) section:
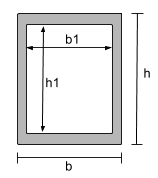
[math] \dfrac{bh^3}{12} – \dfrac{b_1h_1^3}{12} [math]
SkyCiv has put together a handy resource for common Moment of Inertia formula.
Calculators
There are many ways in terms of how to calculate the moment of inertia, one of which is to use software to make the process easier.
SkyCiv Section Builder is a fully capable section design tool that goes far beyond moment of inertia calculator. It also will show you the step-by-step calculations of how to find the moment of inertia:
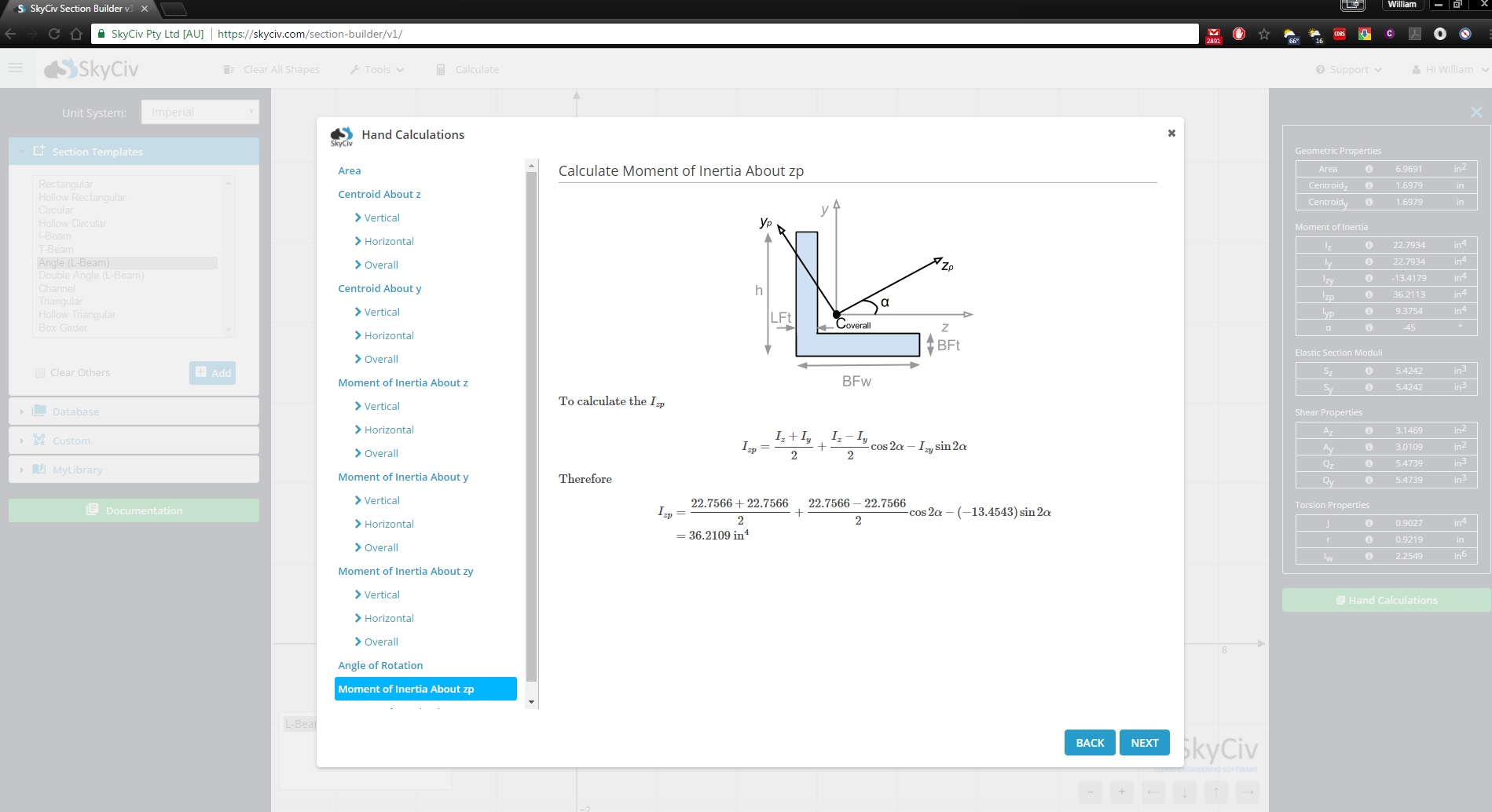
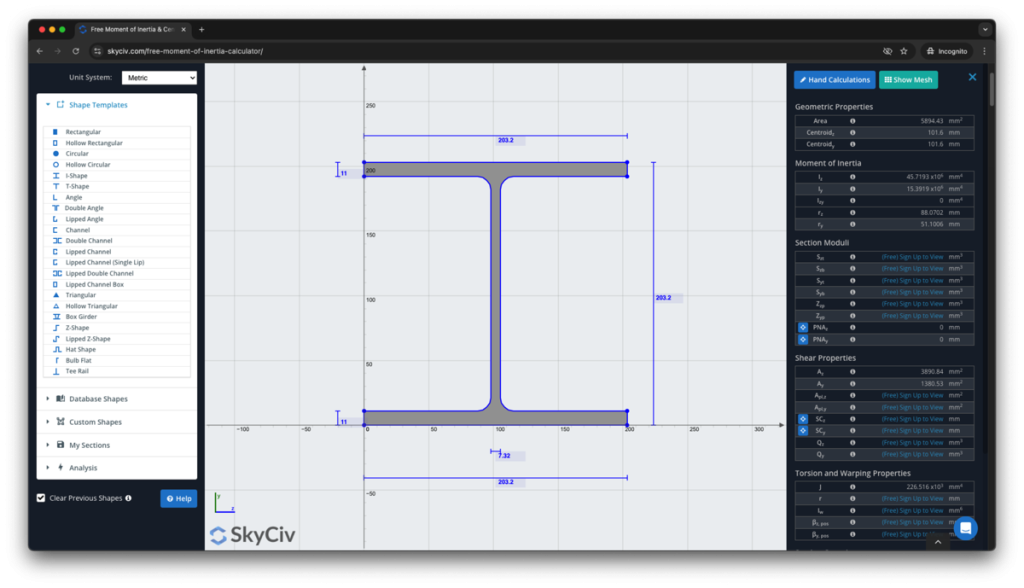
Sign up today to explore more about SkyCiv software, or book a FREE DEMO to get assisted with your engineering projects for existing users!
Additionally, SkyCiv has a free Section Property Calculator as part of the Quick Design library. It’s a simplified tool, but will also calculate the moment of inertia of common section shapes.
Practice Questions
Question 1: Rectangle Section
Problem: Calculate the moment of inertia (Ixx and Iyy) for a rectangular section with a width (b) of 200 mm and a height (h) of 300 mm.
Solution: The formulas for the moment of inertia for a rectangle are:
Substituting the given values:
- b=200 mm
- h=300 mm
For Ixx:
For Iyy:
Question 2: I-Beam
Problem: Calculate the moment of inertia of the major axis (Ixx) of an I-beam section with the following dimensions:
- Top flange width (TFw) = 6 in
- Top flange thickness (TFt) = 0.43 in
- Section Depth = 6 in
- Web thickness (Wt) = 0.29 in
- Bottom flange width (BFw) = 6 in
- Bottom flange thickness (BFt) = 0.43 in
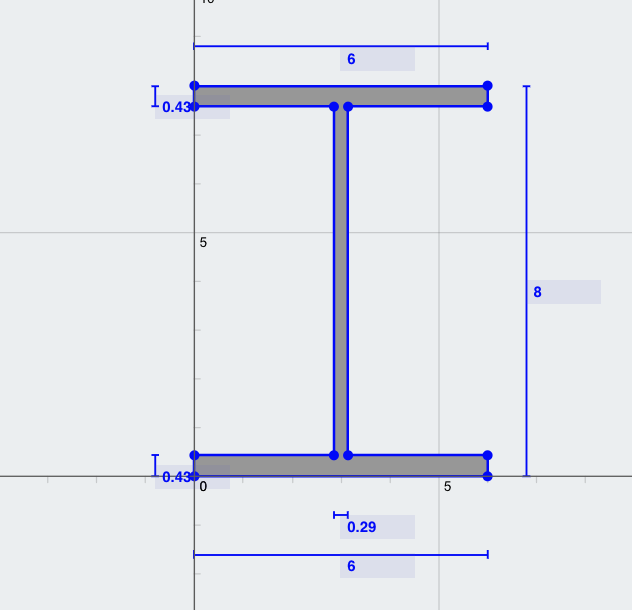
Solution:


