Single pile design in accordance with AS 2159 (2009) & 3600 (2018)

In case of high lateral load or unfavorable soil conditions, pile foundation is more preferred over shallow foundations. Attempts such as soil modification methods can be made to avoid piles, however, these methods may involve expensive processes, wherein this case, piles maybe even cheaper.

SkyCiv Foundation Design module includes the design of piles conforming to American Concrete Institute (ACI 318) and Australian Standards (AS 2159 & 3600).

Want to try SkyCiv’s Foundation Design software? Our free tool allows users to perform load-carrying calculations without any download or installation!

Foundation Design Calculator

Design geotechnical strength of a pile

Vertical loads applied on piles are carried by the end-bearing of the pile and the skin or shaft-friction along its length.  The design geotechnical strength (R_d,g)  is equal to the ultimate geotechnical strength (R_d,ug) multiplied by a geotechnical reduction factor (ø_g) as specified on AS 2159 Section 4.3.1.

\({R}_{d,g} = {ø}_{g} × {R}_{d,ug}\)    (1)

R_d,g = Design geotechnical strength

R_d,ug = Ultimate geotechnical strength

ø_g = Geotechnical reduction factor

Ultimate Geotechnical Strength (R_d,ug)

The ultimate geotechnical strength is equal to the sum of the factored skin friction of the pile (f_m,s ) multiplied by the lateral surface area and base resistance multiplied by the cross-sectional area at the tip of the pile. 

\( {R}_{d,ug} = [{R}_{s} × ({f}_{m,s} × {A}_{s} )] + ({f}_{b} × {A}_{b} )\)    (2)

 R_s = Reduction factor for shaft resistance

 f_m,s = Shaft-frictional resistance

 A_s = Lateral surface area

 f_b = Base resistance term

 A_b = Cross-sectional area at the tip of the pile

For a more detailed guide, check out our article on calculating the skin-frictional resistance and end-bearing capacity.

Geotechnical Reduction Factor (ø_g)

The geotechnical reduction factor is a risk-based calculation for the ultimate design which takes into account different factors, such as site conditions, pile design, and installation factors. Its value ranges commonly from 0.40 to 0.90. AS 2159 4.3.1 also states how to estimate its value as shown in equation (3).

 \( {ø}_{g} = {ø}_{gb} + [K × ({ø}_{tf} – {ø}_{gb})] ≥ {ø}_{gb}  \)     (3)

 ø_gb = Basic geotechnical strength reduction factor

 ø_tf = Intrinsic test factor

K= Testing benefit factor

Intrinsic test and testing benefit factors both rely on which type of load testing used on the piles. Their values are specified in Table 1 and on equations (4) and (5). Pile load testing is discussed briefly in Section 8 of AS 2159.

Intrinsic Test Factor (øtf)
Static load testing	0.90
Rapid load testing	0.75
Dynamic load testing of preformed piles	0.80
Dynamic load testing of other than preformed piles	0.75
Bi-directional load testing	0.85
No testing	0.80

Table 1: Intrinsic Test Factor Values

Testing benefit factor for static load testing:

\( K = \frac{1.33 × p}{p + 3.3}  ≤ 1\)    (4)

Testing benefit factor for dynamic load testing:

\( K = \frac{1.13 × p}{p + 3.3}  ≤ 1\)    (5)

p  = Percentage of the total piles that are tested and meet the acceptance criteria

The basic geotechnical strength reduction factor is evaluated using a risk assessment procedure discussed in Section 4.3. of AS 2159. The outcome of the said procedure is Individual Risk Rating (IRR) and an overall design Average Risk Rating (ARR) which shall be used to determine the value of ø_gb as shown in Table 2.

Basic Geotechnical Strength Reduction Factor (øgb)
Average Risk Rating (ARR)	Risk Category	øgb for low redundancy systems	øgb for high redundancy systems
ARR ≤ 1.5	Very low	0.67	0.76
1.5 < ARR ≤ 2.0	Very low to low	0.61	0.70
2.0 < ARR ≤ 2.5	Low	0.56	0.64
2.5 < ARR ≤ 3.0	Low to moderate	0.52	0.60
3.0 < ARR ≤ 3.5	Moderate	0.48	0.56
3.5 < ARR ≤ 4.0	Moderate to high	0.45	0.53
4.0 < ARR ≤ 4.5	High	0.42	0.50
ARR > 4.5	Very high	0.40	0.47

Table 2: Values for Basic Geotechnical Reduction Factor, (AS 2159 Table 4.3.2)

Low redundancy systems are heavily loaded single piles while high redundancy systems include large pile groups under large pile caps or pile groups with more than 4 piles.

Design Structural Strength

Piles are structurally designed almost the same as a column. Design structural strength (R_d,s) requires ultimate capacities, such as axial and shear forces, and bending moment. The design structural strength of a concrete pile is equivalent to the ultimate design strength (R_us) reduced by a strength reduction factor (ø_s) and a concrete placement factor (k), as stated by Section 5.2.1 of AS 2159.

\( {R}_{d,s} = {ø}_{s} × k  × {R}_{us} \)    (6)

ø_s = Strength reduction factor

k = Concrete placement factor

R_us = Ultimate design strength

The values for the strength reduction factor are shown in Table 3. The concrete placement factor ranges from 0.75 to 1.0, depending on the pile construction method. However, for piles other than concrete and grout, k shall be taken as 1.0.

Strength Reduction Factors (ø)
Axial force without bending	0.65
Bending without axial force (øpb)	0.65 ≤ 1.24 – [(13 × kuo)/12] ≤ 0.85
Bending with axial compression:
(i) Nu  ≥ Nub	0.60
(ii) Nu < Nub	0.60 + {(øpb – 0.66) × [1 – (Nu/Nub)]}
Shear	0.70

Table 3: Strength reduction factors (Table 2.2.2, AS 3600-18)

Axial and flexural capacities of a single pile

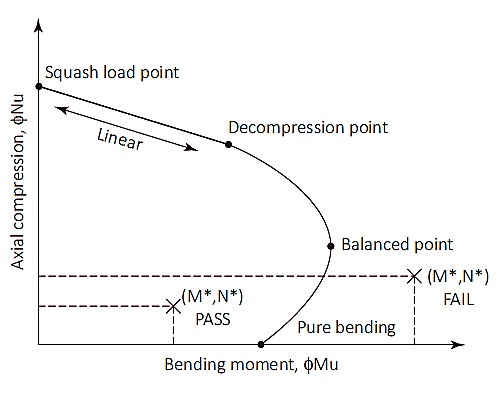
Similar to columns, piles may also be subjected to combined compression and bending load. Axial and flexural capacities are checked using an interaction diagram. This diagram is a visual representation of the behavior of the bending and axial capacities caused by an increase in load from pure bending point until a balanced point is reached.

 

Figure 1: Column interaction diagram

Squash Load (N_uo)

The squash load point is a point on the diagram where the pile will fail in pure compression. At this point, the axial load is applied on the plastic centroid of the section to remain in compression without bending. Squash load (N_uo) and the location of the plastic centroid (d_q) are computed as shown in equations (7) & (8). Although location of the plastic centroid can be taken as 1/2 of the total depth of the cross-section for symmetrical sections with symmetrical reinforcement layout.

\( {ϕN}_{uo} = ø × [({A}_{g} – {A}_{s}) × ({α}_{1} × f’c) + ({A}_{s} × {f}_{sy})]  \)    (7)

A_g = Gross cross-sectional area

A_s = Total area of steel

α₁ = 1.0 – (0.003 × f’c) [0.72 ≤α₁ ≤0.85]

f’c = Concrete strength

f_sy = Yield Strength of steel

\( {d}_{q} =\frac{[(b × D) – {A}_{s}] × ({α}_{1} × f’c) × \sum_{i=1}^{n} ({A}_{bi} × {f}_{sy} × {d}_{yi})}{{N}_{uo}}  \)    (8)

b = Pile cross-sectional width

D = Pile cross-sectional depth or diameter

A_bi = Area of reinforcing bar being considered

d_yi = Depth of reinforcing bar being considered

Squash load point through to decompression point

Decompression point is where the concrete strain at the extreme compressive fibre is equal to 0.003 and the strain in the extreme tensile fibre is zero. Strength of the pile between the squash load and the decompression points can be calculated by linear interpolation with strength reduction factor (ø_s) of 0.6.

Decompression point through to pure bending

Pure bending point is where the axial load capacity is zero. The transition from decompression point to pure bending uses a strength reduction factor of 0.6 to 0.8 and an input parameter (k_u) is introduced. The value of k_u starts at 1 at decompression point and decreases until pure bending is reached. Between the transition of the two points, a balanced condition is achieved. At this point, the concrete strain is at its limit (ε_c=0.003) and the outer steel strain reaches yield (ε_s=0.0025), The value of k_u at this point is approximately 0.54 with a strength reduction factor of 0.6.

Once a value of k_u is selected, tensile and compressive forces of the section can be calculated. The axial load on the section is equivalent to the sum of tensile and compressive forces, while the bending moment is calculated by resolving these forces about the neutral axis. Calculation for the compressive and tensile forces are enumerated below

Force due to concrete (F_cc):

\( {F}_{cc} =  {α}_{2} × f’c × {A}_{c}  \)    (9)

α₂ = 0.85 – (0.0015 × f’c) [α_2 ≥0.67]

A_c = Compression block area (refer to Figure 2) 

= b × γ × k_u × d (rectangular cross-section)

=(1/2) × (θ – sinθ) × (D/2)² (circular cross-section)

γ = 0.97 – (0.0025 × f’c) [γ _≥0.67]

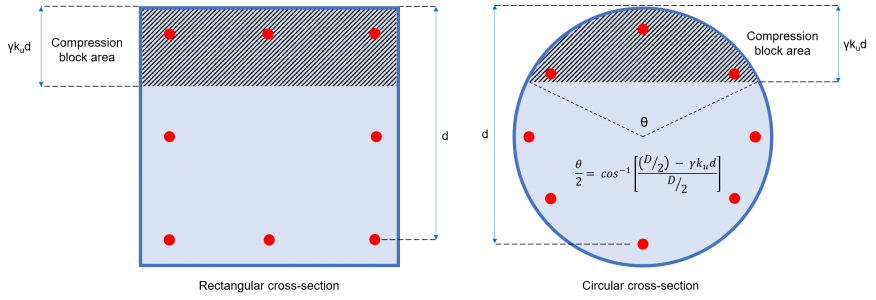
Figure 2: Concrete Compression Block Area

Force (F_si) and moment (M_i) contributed by each individual bar:

Each reinforcing bar of the section exerts a force that could either be compressive or tensile, depending on the value bar strain (ε_si) shown in equation (10).

\( {ε}_{si} = \frac{{ε}_{c}}{({k}_{u} × d)} × [({k}_{u} × d) – {d}_{yi}]  \)    (10)

d_yi = Depth to the bar being considered

ε_c= Concrete strain = 0.003 

If ε_si < 0 (bar is in tension)

If ε_si > 0 (bar is in compression)

Bar in compression:

\( {F}_{si} = {σ}_{si} × {A}_{bi}    \)    (11)

σ_si = Stress in bar = Minimum [(ε_si × E_s ), f_sy]

E_s = Modulus elasticity of steel

A_bi = Bar area

Bar in tension:

\( {F}_{si} = [{σ}_{si} – ({α}_{2} × f’c)] ×  {A}_{bi}    ≥ 0\)    (12)

σ_si = Stress in bar = Minimum [(ε_si × E_s ), –f_sy]

E_s = Modulus elasticity of steel

A_bi = Bar area

Moment by each bar:

\( {M}_{i} = {F}_{si} × {d}_{yi} \)    (13)

Axial capacity of the pile:

\( {øN}_{u} = ø × [ {F}_{cc} + {Σ}_{i=1}^{n} {F}_{si}]\)    (14)

Flexural capacity of the pile:

\( {øM}_{u} = ø × [ ({N}_{u} × {d}_{q}) – ({F}_{cc} × {y}_{c}) – {Σ}_{i=1}^{n} {M}_{i}] \)    (15)

Design bending moment:

Section 7.2 specifies that piles are required to have a out-of-position tolerance of 75mm for the horizontal positioning of the piles. This requirement may induce a bending moment equal to axial load multiplied by the eccentricity of 75mm. Additionally, a minimum design moment shall also be considered which is equivalent to the axial force multiplied by 5% of the overall minimum width of the pile. Therefore, the design bending moment should be the greater value between equations 16a and 16b.

\( {M}_{d} = {{M}^{*}}_{applied} +  ({N}^{*} × 0.075 m)  \)    (16a)

\( {M}_{d} =  {N}^{*} × (0.05 × D)  \)    (16b)

M_d = Design bending moment

M*_applied = Applied moment

N* = Axial load

D = Pile width

Shear capacity of a single pile

Calculation for the strength in shear shall be in accordance with Section 8.2 of AS 3600. Shear strength is equivalent to a combined shear capacities of the concrete and the steel reinforcement (equation 17).

\( {øV}_{u} = ø × ({V}_{uc} + {V}_{us}) ≤ {øV}_{u,max} \)    (17)

Shear strength of concrete (V_uc)

The contribution of concrete to the shear capacity is computed as shown on equation (18) which is defined on Section 8.2.4.1 of AS 3600. This section also requires the value of √f’c shall not exceed 9.0 MPa. The values for the parameter k_v and θ_v  are determined by using a simplified method suggested by Section 8.2.4.3 of AS 3600.

\( {V}_{uc} = {k}_{v} × b × {d}_{v} × \sqrt{f’c} \)    (18)

d_v = Effective shear depth = Maximum [(0.72 × D ), (0.90 × d )]

Determination of the minimum area of shear reinforcement (A_sv.min) & k_v:

The area of the shear reinforcement (A_sv) is the total bar area of all the provided steel bars tied in the same direction of the applied load. Section 8.2.1.7 of AS 3600 provided the equation for the minimum transverse shear reinforcements, which shall be:

\( \frac{{A}_{sv.min}}{s} = \frac{0.08 × \sqrt{f’c} × b}{{f}_{sy.f}}  \)

f_sy.f = Yield strength of shear reinforcing bars 

s= Center-to-center spacing of shear reinforcing bars 

For (A_sv/s) < (A_sv.min/s):

\( {k}_{v} = \frac{200}{[1000 + (1.3 × {d}_{v} )]}  ≤ 0.10\)

For (A_sv/s) ≥ (A_sv.min/s):

\( {k}_{v} = 0.15 \)

Shear strength of steel bars (V_us)

The contribution of the transverse shear reinforcements to the shear capacity calculated is shown in equation (19), which is defined in Section 8.2.5 of AS 3600.

\( {V}_{us} = \frac{{A}_{sv} × {f}_{sy.f} × {d}_{v}}{s} × cot{θ}_{v} \)    (19)

θ_v= angle of inclination of the compression strut = 36º

Maximum shear strength (V_u.max)

Shear capacity is limited and in no case shall exceed the maximum value specified on Section 8.2.6 of AS 3600 (equation 20).

\( {V}_{u.max} = 0.55 × [ (f’c × b × {d}_{v}) × \frac{cot{θ}_{v} + cot{α}_{v}}{1 + cot^{2}{θ}_{v} }]  \)    (20)

α_v= angle between the inclined shear reinforcement and the longitudinal tensile reinforcement≈ 90º

Ultimate shear strength (V_u)

The total shear strength contributed by the concrete and shear reinforcements shall be less than or equal to the limiting value of V_u.max

\( {V}_{u} = ({V}_{uc}  + {V}_{us} ) ≤ {V}_{u.max}   \)    (21)

Design shear strength (øV_u)

Capacity reduction factor that shall be applied for the ultimate shear strength is ø = 0.7. Therefore, the design shear strength of the pile is given by:

\( {øV}_{u} = ø × ({V}_{uc}  + {V}_{us} )  \)    (22)

References

• Pack, Lonnie (2018). Australian Guidebook For Structural Engineers.  CRC Press.
• Piling Design and Installation (2009). AS 2159. Australian Standard
• Concrete Structures (2018). AS 3600. Australian Standard