Section Property Calculator

The above centroid calculator will use the relevant centroid equations to find the centroid of a circle, rectangle, hollow rectangular, I Beams, Channels and Angle sections. The calculator will return simplified results including the centroid (in both X and Y directions) from a few simple section dimension inputs. The section centroid is the geometric centre of a shape, representing the point where its area can be evenly balanced. Assuming a consistent material within the section, it will be the centre of gravity for that section. The centroid is usually defined in terms of Cx and Cy, to represent the distance from the bottom of the section in x and y respectively. So the centroid location can be denoted as a point [Cx, Cy].

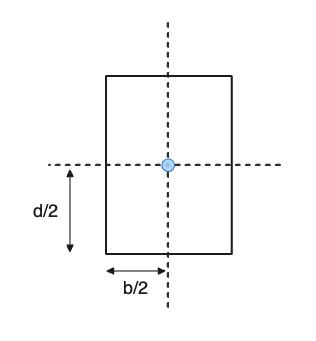
For some shapes, this is quite a simple calculation. For instance, finding the centroid of a rectangle is as simple as halving the height and width:

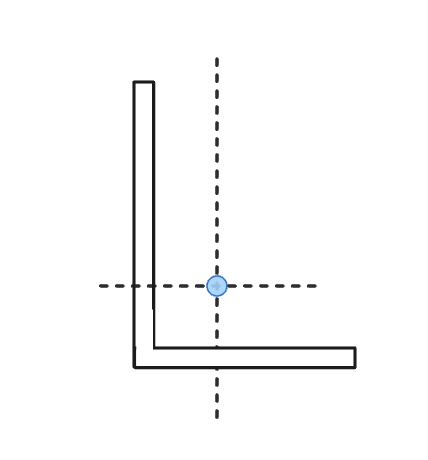
However, for more complex sections where they are not symmetrical in both axis, the centroid calculations are a little more complex. For instance, an Angle Section may have it's centroid somewhere off the actual section:

The section modulus is an important geometric property, which ultimately represents how well a section can resist bending. It's calculated by the following simple elastic section modulus equation:

S_xb = I_xx / Cy

The above section modulus formula is for the elastic section modulus about the x-axis to the most bottom fibre of the section. Section modulus properties are often broken into four results, with individual results for:

• S_xb: Section Modulus about x-axis to the bottom of the section
• S_xt: Section Modulus about x-axis to the top of the section
• S_yt: Section Modulus about y-axis to the top of the section (or the right-most part of the section)
• S_yb: Section Modulus about y-axis to the bottom of the section (or the left-most part of the section)

It's also important to note, the x/z axis can be used interchangeably. So for instance, in our section modulus calculations, we use z instead of x as our horizontal axis.

Elastic Section Modulus (S) Vs Plastic Section Modulus (Z)

The elastic section modulus (S) represents a section's bending behavior within its elastic limit - where it deforms under load but returns to its original shape once the load is removed. This modulus is crucial for calculating maximum bending stress before yielding.

On the other hand, the plastic section modulus (Z) captures a section's bending behavior beyond its elastic limit, where it undergoes plastic deformation. Z represents the member's ability to redistribute stress post-yielding, enhancing its resistance to bending.

While S (elastic) is fundamental for designing structures operating within their elastic range, Z (plastic) finds application in scenarios where plastic behavior is anticipated or desired, such as in steel design when dealing with compact sections, the Plastic Section modulus can be used to push the design further. In the case of a non-compact section, the section will locally buckle before its plastic moment capacity is reached - hence the elastic section modulus is used in this case. You can read more about this in SkyCiv's guide to AS4100 Steel Design, although this makes specific references to the Australian Standards, it has useful general comments about section classifications in steel design.

It's also important to note that different regions adopt different nomenclature for plastic and elastic modulus:

Australia
Z = Elastic, S = Plastic

America + Rest of World
S = Elastic, Z = Plastic

• Aluminum Design Software
• AISC 360 I Beam Load Capacity Calculator
• CSA O86-14 Wood Design Software
• Eurocode 5 Timber Design Software
• AS 4100:2020 Steel Design Software