How to Calculate Moment of Inertia of a Beam Section (Second Moment of Area)
Before we find the moment of inertia of a beam section (also known as second moment of area of a beam section), its centroid (or center of mass) must be known. For instance, if the moment of inertia of the section about its horizontal (XX) axis was required then the vertical (y) centroid would be needed first (Please view our tutorials on calculating the centroid of a beam section and calculating the statical/first moment of area).
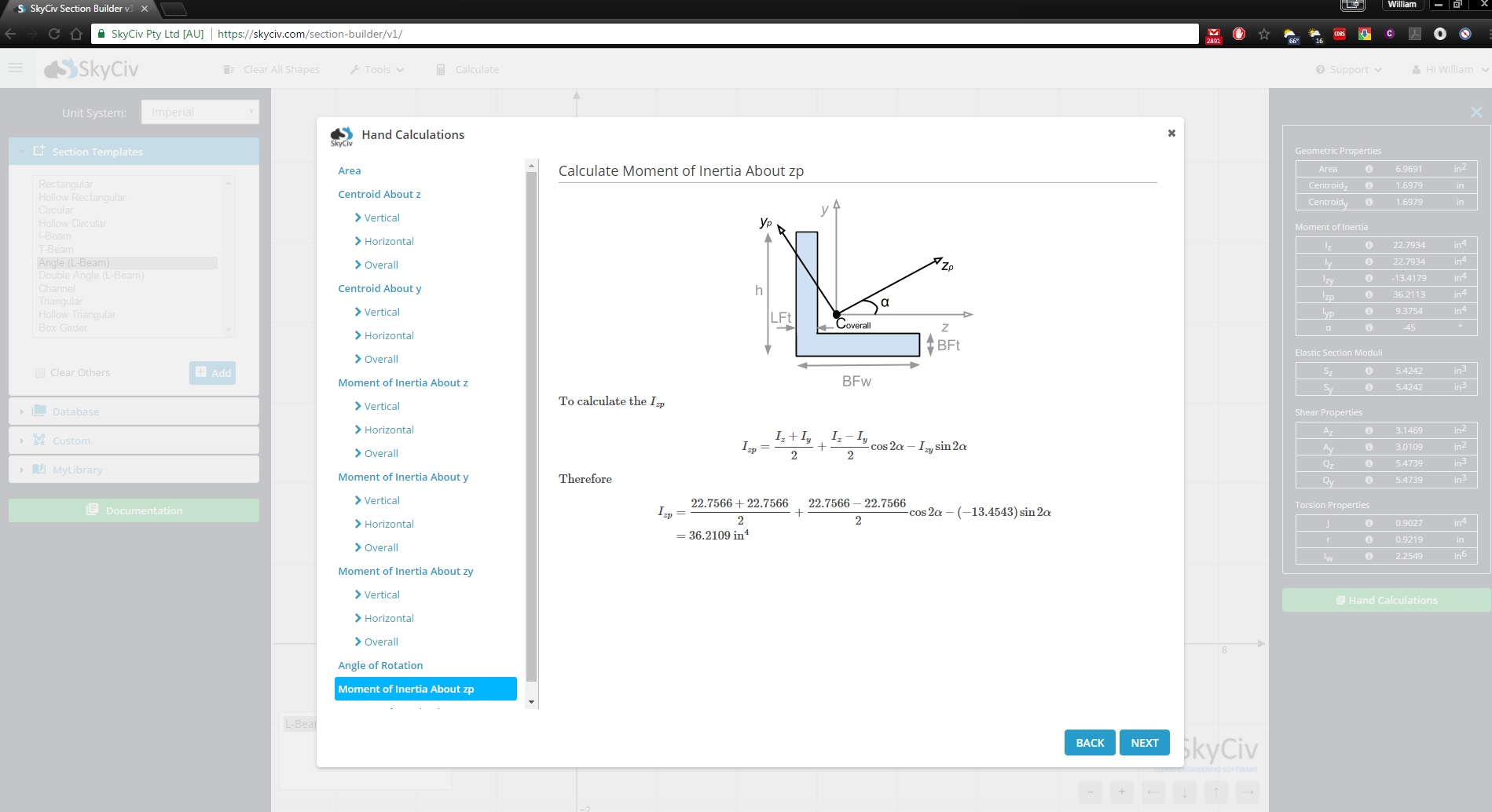
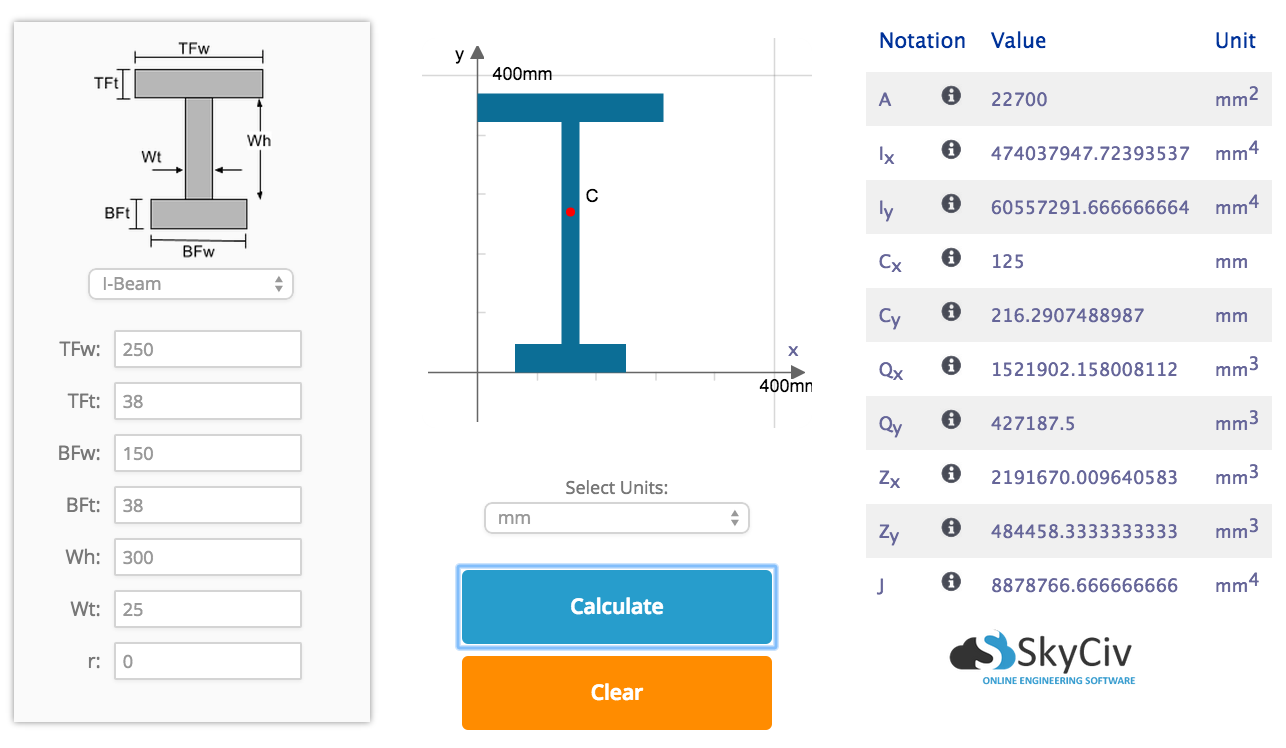
Before we start, if you were looking for our Free Moment of Inertia Calculator please click the link to learn more. This will calculate the centroid, moment of inertia, and other results and even show you the step-by-step calculations! But for now, let’s look at a step-by-step guide and example of how to calculate the moment of inertia:
Step 1: Segment the beam section into parts
When calculating the area moment of inertia, we must calculate the moment of inertia of smaller segments. Try to break them into simple rectangular sections. For instance, consider the I-beam section below, which was also featured in our centroid tutorial. We have chosen to split this section into 3 rectangular segments:
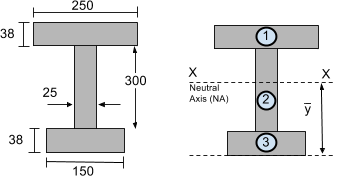
Step 2: Calculate the Neutral Axis (NA)
The Neutral Axis (NA) or the horizontal XX axis is located at the centroid or center of mass. In our centroid tutorial, the centroid of this section was previously found to be 216.29 mm from the bottom of the section – this is covered in our how to find the centroid of a shape tutorial. These can also simply be calculated from our centroid calculator or from common centroid equations.
Calculating the centroid, or Neutral Axis, is essential in how to calculate moment of inertia of a beam, as this is the axis at which the moment of inertia acts.
Step 3: Calculate Moment of Inertia
To calculate the total moment of inertia of the section we need to use the “Parallel Axis Theorem”:

Since we have split it into three rectangular parts, we must calculate the moment of inertia of each of these sections. It is widely known that the moment of inertia equation of a rectangle about its centroid axis is simply:
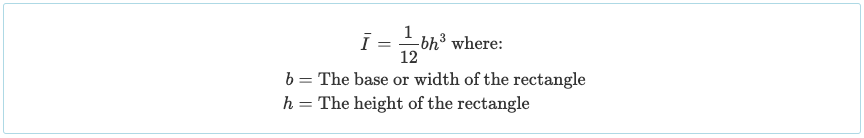
The moment of inertia of other shapes is often stated in the front/back of textbooks or from this guide of the moment of inertia shapes. However the rectangular shape is very common for beam sections, so it is probably worth memorizing.
Now we have all the information we need to use the “Parallel Axis Theorem” and find the total moment of inertia of the I-beam section. In our moment of inertia example:

So there you have our guide on calculating the area of moment for beam sections. This result is critical in structural engineering and is an important factor in the deflection of a beam. We hope you enjoyed the tutorial and look forward to any comments you have.
Free Moment of Inertia Calculator
There are many ways in terms of how to calculate the moment of inertia, one of which is to use software to make the process easier. As a side note: Sometimes this is incorrectly defined as second moment of inertia, however this is incorrect. The two names for this results are: moment of inertia, or second moment of area.
SkyCiv Section Builder provides you with full calculations of the moment of inertia. This interactive module will show you the step-by-step calculations of how to find the moment of inertia: