How to Calculate Factor of Safety Against Sliding for Retaining Wall – Reinforced Concrete Cantilever
This retaining wall sliding calculation example is a simple guide on how to calculate the Factor of Safety against sliding in a retaining wall as part of the stability checks. This sliding check is performed to ensure that the resulting force of the friction between the wall and the substructure soil is enough to prevent the Retaining Wall from sliding as a result of the horizontal loads rising from the retained soil active pressure. Basically, the friction force that will prevent the wall from sliding is the total vertical load multiplied by the Soil-Concrete Friction Coefficient defined for the substructure soil material and the sliding force is the result of the retained soil’s lateral pressure and the pressure associated with the surcharge presence.
That said, the calculation process will be detailed in the following:
Input data:
Stem
- Height: 3.124 m
- Width: 0.305 m
- Offset: 0.686 m
Base
- Width: 2.210 m
- Thickness: 0.381 m
Active and Passive Soil
- Unit weight: 18.85 kN/m3
- Friction Angle: 35 degrees
Substructure Soil
- Unit weight: 18.85 kN/m3
- Friction Angle: 35 degrees
- Soil-Concrete Friction Coefficient: 0.55
- Allowable bearing pressure: 143.641 kPa
Soil Layers:
- Active: 3.505 m
- Passive: 0.975 m
- Substructure: 0.792 m
Surcharge Load Value: -17.237 kN/m
All the loads associated with the Retaining Wall Sliding Calculation are shown in the following picture:
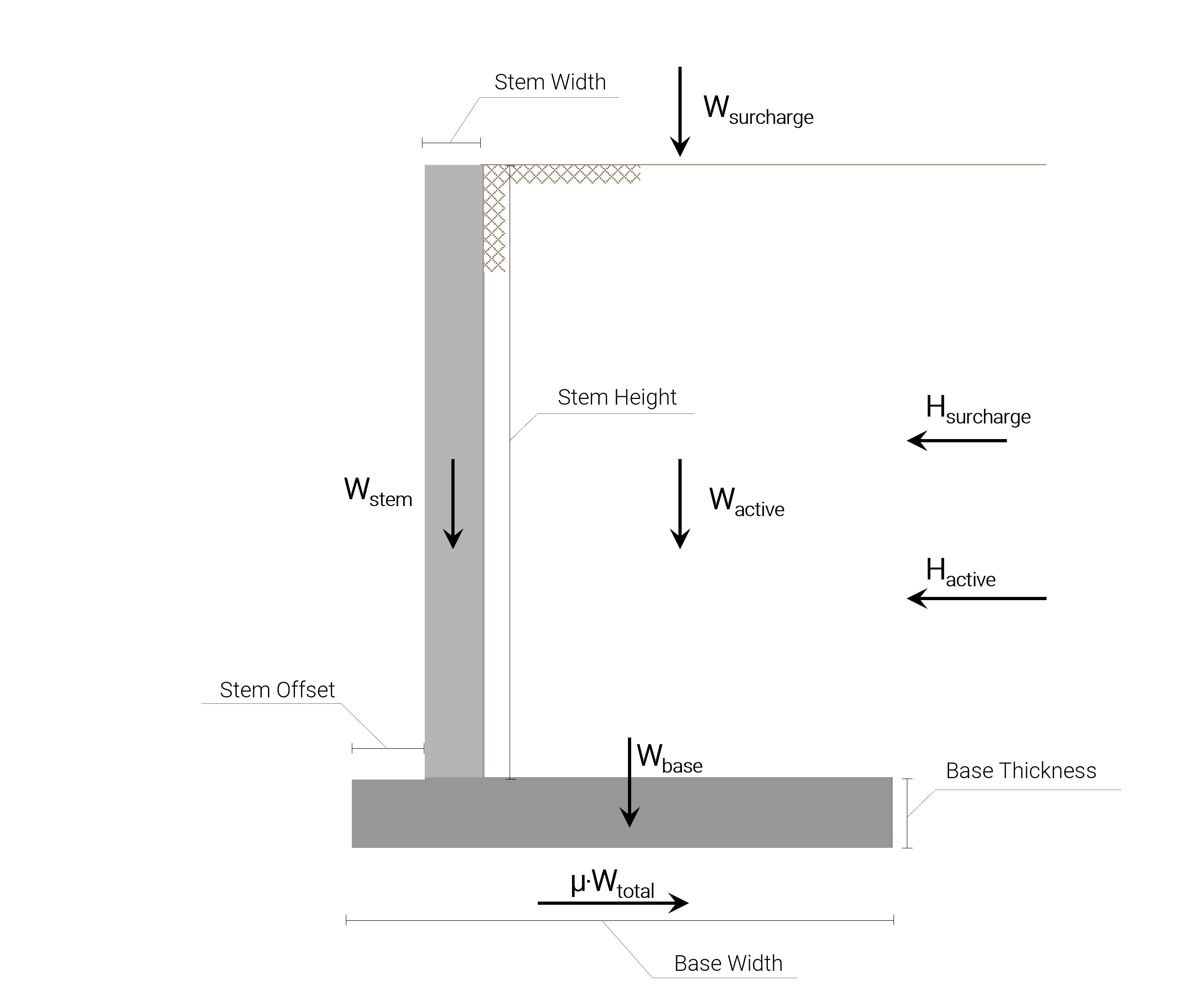
Sliding force
As mentioned, the sliding force is the sum of the resultant horizontal force from the active soil pressure in the active soil side and the resultant horizontal force from the presence of the surcharge.
In order to calculate the lateral earth pressure due to the retained soil active pressure and the surcharge resultant lateral pressure, it is necessary to calculate the Rankine active earth-pressure coefficient:
\( K_a = \frac{1-\sin(\gamma_{soil,\;active})}{1+\sin(\gamma_{soil,\;active})} \)
\( K_a = \frac{1-\sin(35º)}{1+\sin(35º)} = 0.271 \)
With that result, it is now possible to calculate the horizontal load resulting from the lateral active pressure that the retained soil exerts:
\(H_{active} = \frac{1}{2} \cdot \gamma_{soil,\;active} \cdot (stem_{height} + base_{thickness})^{2} \cdot K_a \)
\(H_{active} = \frac{1}{2} \cdot 18.85\;kN/m^3 \cdot 3.505^{2} \cdot 0.271 \)
\(H_{active} = 31.377\;kN/m \)
For calculating the horizontal force related to the surcharge presence, an equivalent soil height is calculated first, and then the actual force:
\( h_{soil,\;eq} = \frac{surcharge_{value}}{\gamma_{soil,\;active}} = \frac{17.237 \;kN/m}{17.237 \;kN/m} \)
\( h_{soil,\;eq} = 0.914 \; m \)
\( H_{surcharge} = \gamma_{soil,\;active} \cdot h_{soil,\;eq} \cdot (stem_{height} + base_{thickness}) \cdot K_a\)
\(H_{surcharge} =\cdot 18.85\;kN/m^3 \cdot 0.914 \; m \cdot 3.505 \; m \cdot 0.271 \)
\(H_{surcharge} = 16.372\;kN/m \)
With those two loads calculated, it is now possible to calculate the sliding force by summing the two loads up:
\( \Sigma{H} = H_{active} + H_{surcharge} = 31.377\;kN/m + 16.372\;kN/m \)
\( \Sigma{H} = 47.749 \; kN \)
Friction force
In order to calculate the friction force that resists the sliding force, it is necessary to evaluate the total vertical load first:
\(W_{stem} = \gamma_{concrete} \cdot (stem_{height} \cdot stem_{width} ) = 23.58 \;kN/m^3 \cdot 3.124\;m \cdot 0.305\;m\)
\( W_{stem}= 22.467\;kN/m\)
\(W_{base} = \gamma_{concrete} \cdot (base_{thickness} \cdot base_{width} ) = 23.58 \;kN/m^3 \cdot 0.381\;m \cdot 2.210\;m\)
\( W_{base}= 18.855\;kN/m\)
\(W_{active} = \gamma_{soil,\;active} \cdot (stem_{height}\cdot (base_{width}-stem_{offset}-stem_{width}) ) \)
\( W_{active} = 18.85 \;kN/m^3 \cdot 3.124\;m \cdot (2.210-0.686-0.305)\;m\)
\( W_{active} = 71.784\;kN/m\)
\(W_{surcharge} = surcharge_{value} \cdot ( (base_{width}-stem_{offset}-stem_{width} ) \)
\( W_{surcharge} = 17.237 \;kN/m \cdot (2.210-0.686-0.305)\;m\)
\( W_{surcharge} = 21.012\;kN/m\)
Having all those individual loads it is now possible to calculate the friction force:
\( \mu \cdot \Sigma{W} = \mu \cdot (W_{stem}+W_{base}+W_{active}+W_{surcharge}) \)
\( \mu \cdot \Sigma{W} = 0.55 \cdot (22.467+18.855+71.784+21.012)\;kN \)
\( \mu \cdot \Sigma{W} = 0.55 \cdot 135.12\;kN \)
\( \mu \cdot \Sigma{W} = 74.315\;kN \)
Factor of Safety against sliding
Finally, the Factor of Safety against sliding for the retaining wall will be the ratio between the friction and the sliding forces. ACI 318 recommends a factor of safety to be greater than or equal to \(1.5\):
\( FS = \frac{\mu \cdot \Sigma{W}}{\Sigma{H}} \)
\( FS = \frac{74.315\;kN}{47.749 \; kN}= 1.556 \ge 1.5\) PASS!
Retaining Wall Calculator
SkyCiv offers a free Retaining Wall Calculator that will check sliding in retaining wall and perform a stability analysis on your retaining walls. The paid version also displays the full calculations, so you can see step-by-step how to calculate the stability of retaining wall against overturning, sliding and bearing!
Related Tutorial
Product Developer
BEng (Civil)



