A guide to Static Determinacy, Indeterminacy, and Instability

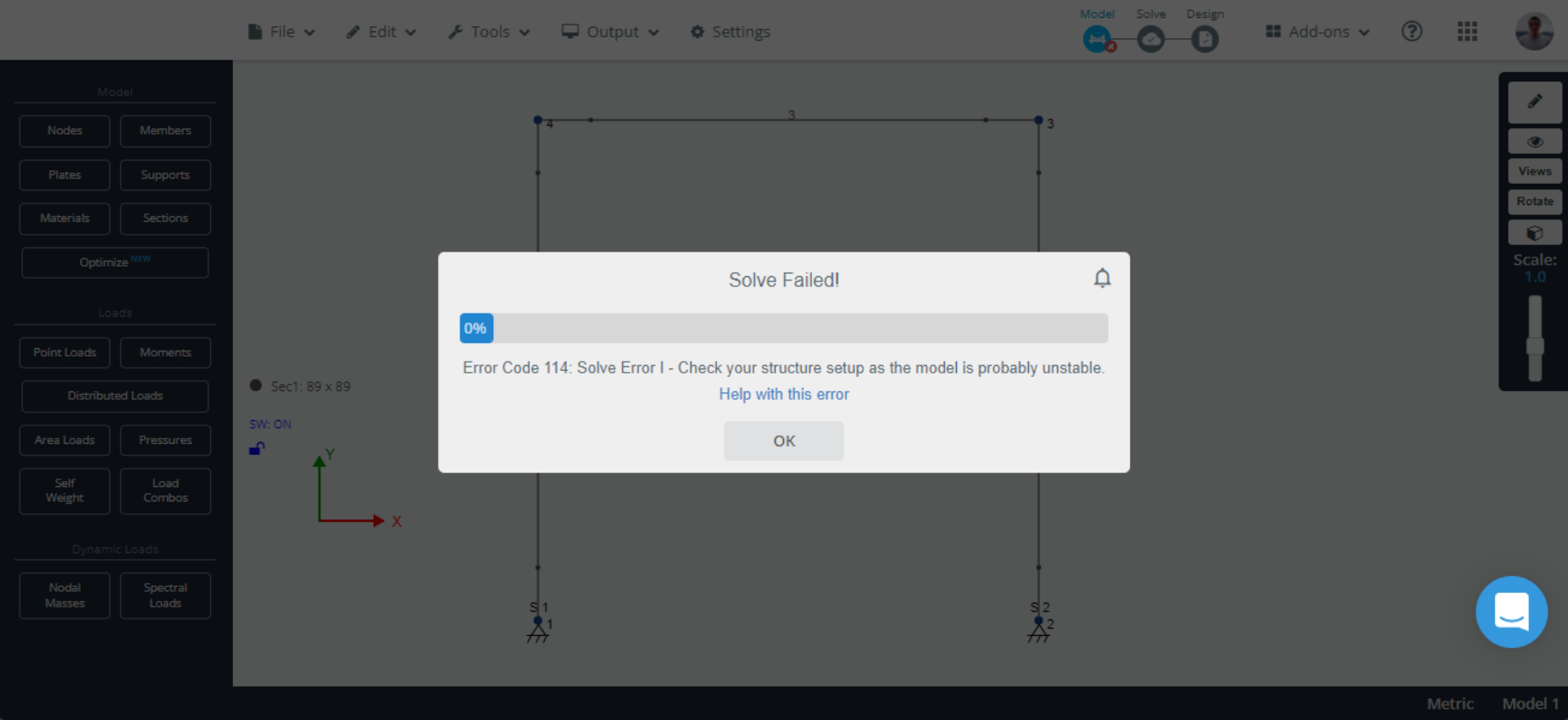
Once the structure is completely modeled and the loads are applied, it is time to solve the system to find all the results that come from the analysis stage: reactions, internal forces (shear force, bending moment, axial force, and torsion), displacements, and stresses. Sometimes things do not go as expected and when it comes to solving, you may get an annoying message saying “Solve Failed! Check your structure set up, as the model is probably unstable”, and chances are that you do not know exactly what is wrong with the model. This article explains the concept of structural stability along with static determinacy and indeterminacy which are very related topics, it also presents some tips for troubleshooting an unstable model.

In general, a structure is considered internally stable if it holds its shape when supports are removed. Conversely, a structure is considered internally unstable if once it is detached from the supports, the structure cannot maintain its shape and may undergo large displacements or even collapse. That said, we will have a closer look at the static determinacy formula, both for internally unstable and stable structures. The static determinacy formula helps to classify a structure as externally unstable, statically determinate, or statically indeterminate.

Static determinacy of internally stable structures

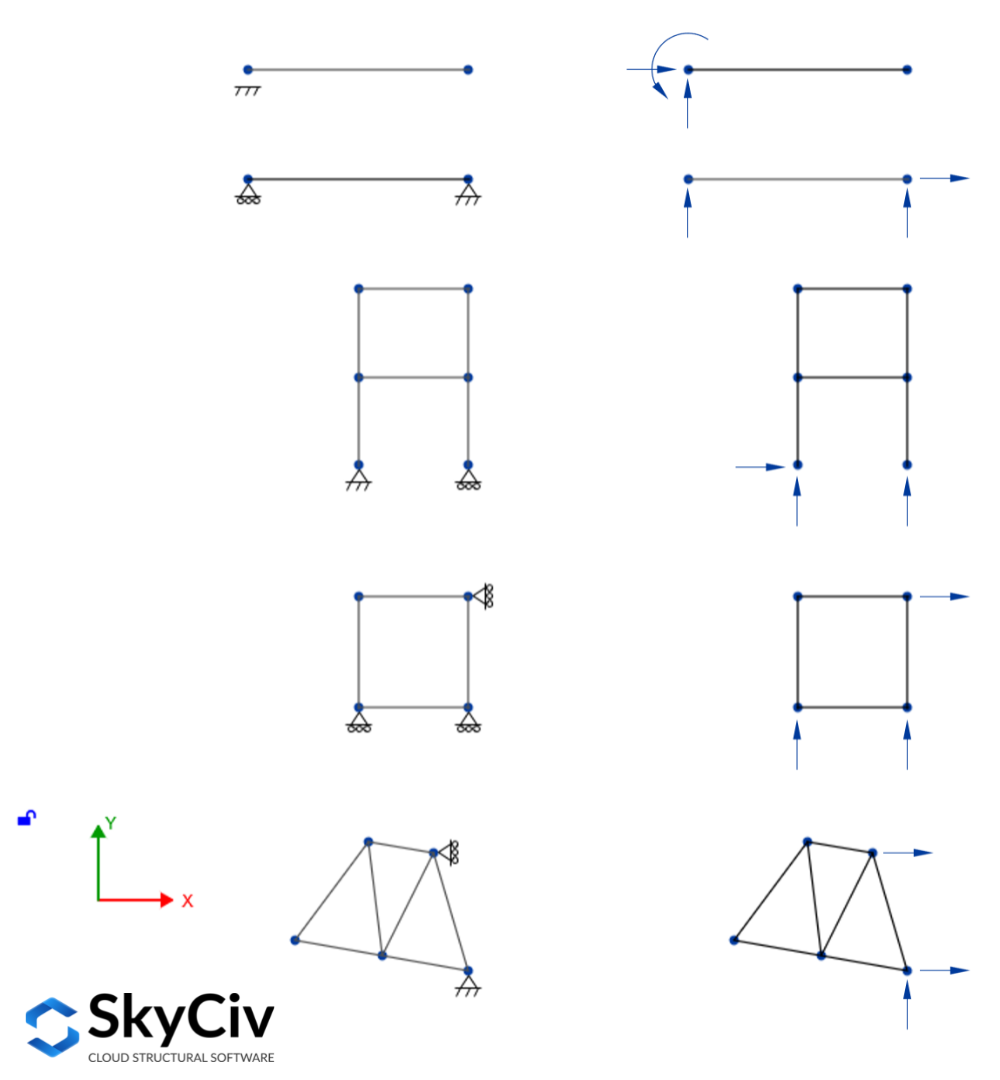
An internally stable structure can be taken as statically determinate externally if all its support reactions can be solved by solving the equations of equilibrium. For planar structures under in-plane loads, there need to be three supporting reactions for the structure to be in equilibrium. Additionally, since there are only three equilibrium equations available, three reactions can be found at the most, so there should be exactly three reactions supporting the plane structure. Some examples of externally statically determinate planar structures are shown in the following picture:

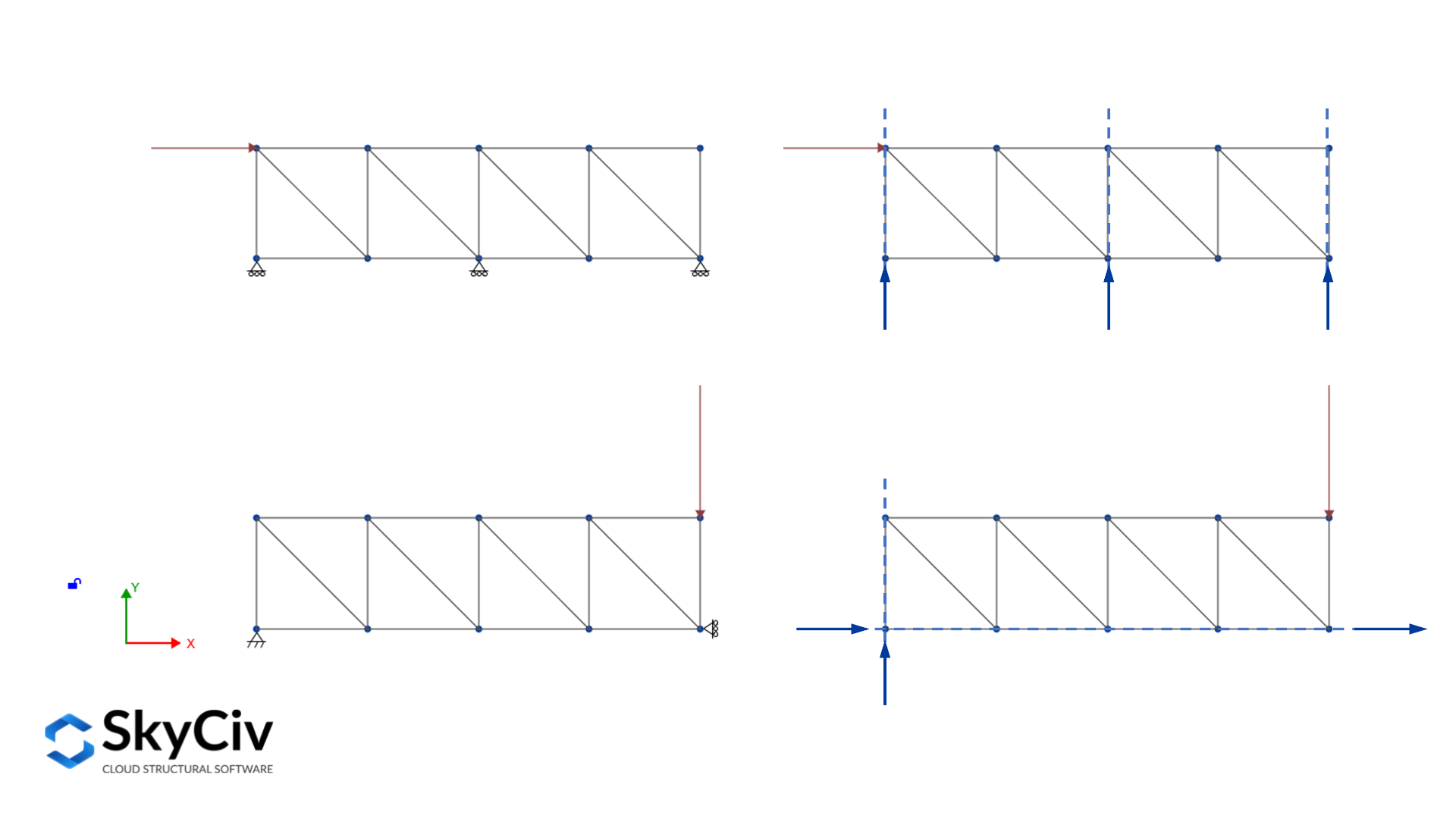
When more than three reactions are supporting the structure, it is called a statically indeterminate externally structure, since it is not possible to solve all the reactions using the three equations of equilibrium. Those reactions are called external redundant and the number of external redundant is known as the degree of external indeterminacy, written as an equation it looks like this:

\(i_e = r – 3\)

Where \(r\) is the number of reactions that support the structure.

In the cases that the structure is supported by less than three support reactions, those are not enough for preventing the structure from moving on its plane, since that structure would not remain in equilibrium under a general system of loads it is called a statically unstable externally. Based on the number of reactions \(r\), it is possible to determine the static determinacy, indeterminacy, and instability of internally stable structures using the criteria that follows:

\( r \begin{cases} < 3, \; \textrm{statically unstable externally structure} \\ = 3, \; \textrm{statically determinate externally structure} \\ > 3, \;  \textrm{statically indeterminate externally structure} \end{cases}\)

It is important to mention that once the last two conditions are fulfilled, it is not assured that the structure will be stable. It means that even when the structure is supported by more than three reactions if supports and not arranged properly the structure might still be unstable. This is called  geometrical external instability and is caused by two main reasons:

• When all the reactions’ lines of action are parallel because the structure will not be prevented from displacing in the perpendicular direction of the reactions
• When all the reactions’ lines of action are concurrent at one point because the structure will be allowed to rotate about the concurrency point

Static determinacy of internally unstable structures

Internally unstable structures are those that when detached from the supports cannot hold their original shape. Without supports, the members of the structure would undergo large displacements with respect to each other. To define the static determinacy, indeterminacy, and external stability of these structures, the equations change due to the additional equations of condition that come into play accounting for the special connections between members. The special connections are those that do not transmit moment, shear force, or axial force.

As an example, consider the structure in the picture below (top section), it is clearly supported by three reactions, but those are not enough for guaranteeing equilibrium under the applied in-plane forces thanks to the presence of the hinge between the members, it needs a fourth non-parallel, non-concurrent reaction to ensure equilibrium (bottom section).

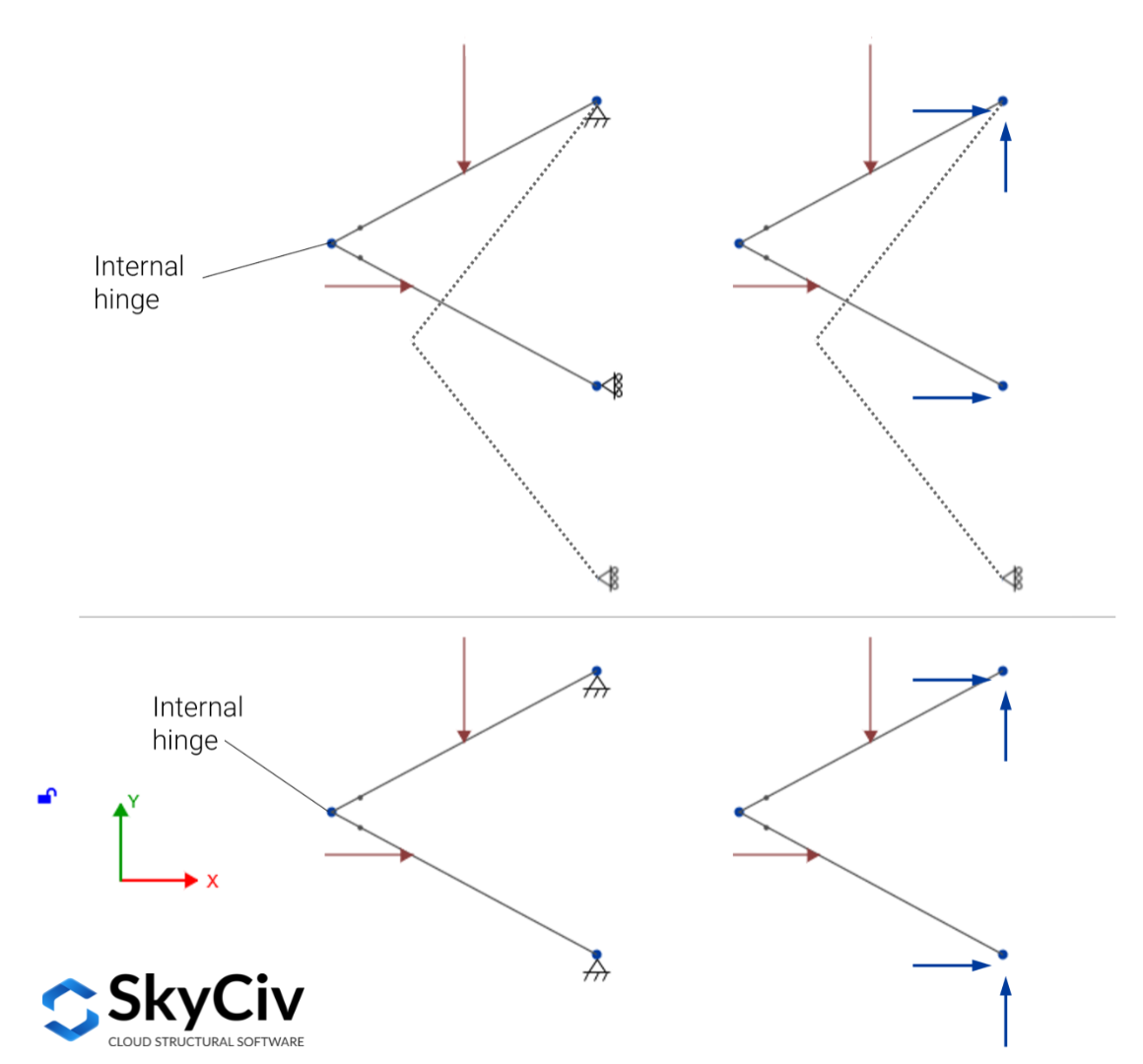
In general, for internally unstable structures, based on the number of reactions \(r\) and equations of condition \(e_c\), it is possible to determine the static determinacy, indeterminacy, and instability of internally stable structures using the criteria that follows:

\( r \begin{cases} < 3 + e_c, \; \textrm{statically unstable externally structure} \\ = 3 + e_c, \; \textrm{statically determinate externally structure} \\ > 3 + e_c, \;  \textrm{statically indeterminate externally structure} \end{cases}\)

For indeterminate externally internally unstable structures, the degree of external indeterminacy can be expressed as follows:

\(i_e = r – (3 + e_c)\)

Wrap-up

For planar structures that are internally stable to be externally stable, meaning that it remains in equilibrium under a general system of loads, the following must hold:

• The structure is supported by three or more reactions
• All the reactions cannot be parallel nor concurrent

For planar structures that are internally unstable to be externally stable, meaning that it remains in equilibrium under a general system of loads, the following must hold:

• The number of reactions supporting the structure is greater than or equal to the number of equations of condition plus three
• All the reactions cannot be parallel nor concurrent

Troubleshooting an unstable structure in S3D

There are a few things you can try when the model is not solving, and you are getting the “Unstable structure” error message:

• Select all the members and ensure they have their member end fixities as “FFFFFF”, and try to run the model. If some members need to have a different end fixity in the final model, start changing it one by one and solve the structure to see which is the exact member or set of members causing the instability.
• Select all the members and change their type from normal to continuous, which would properly connect members that do not have a node in the intersection but are meant to be connected.
• Suppress from the analysis all the cables, and try to solve the model. To learn how to suppress members, refer to this article.

References

Kassimali, Aslam. “3.4 Static Determinacy, Indeterminacy, and Instability.” Structural Analysis, Cengage Learning, 2011.