A fully worked example of IS 875-3 wind load calculations

In this article, an example wind load pressure calculation for a building in Walwane, Maharashtra, India (18.945695° N, 74.564866° E) will be shown. This calculation will be in accordance with IS 875-3:2015 wind load calculations. SkyCiv free wind load calculator recently added the IS 875-3 wind load calculations, hence, we are going to demonstrate how to calculate the wind loads, by using an S3D Barnhouse model below:

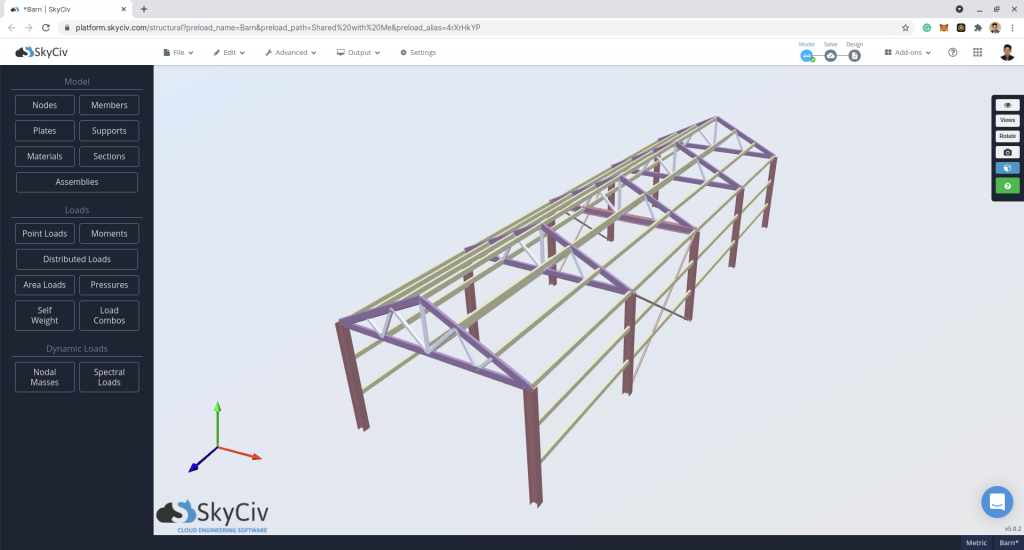
For this case study, the structure data are as follows:

Location	Walwane, Maharashtra, India (18.945695° N, 74.564866° E)
Occupancy	Miscellaneous – Farm structure
Terrain	Flat open land
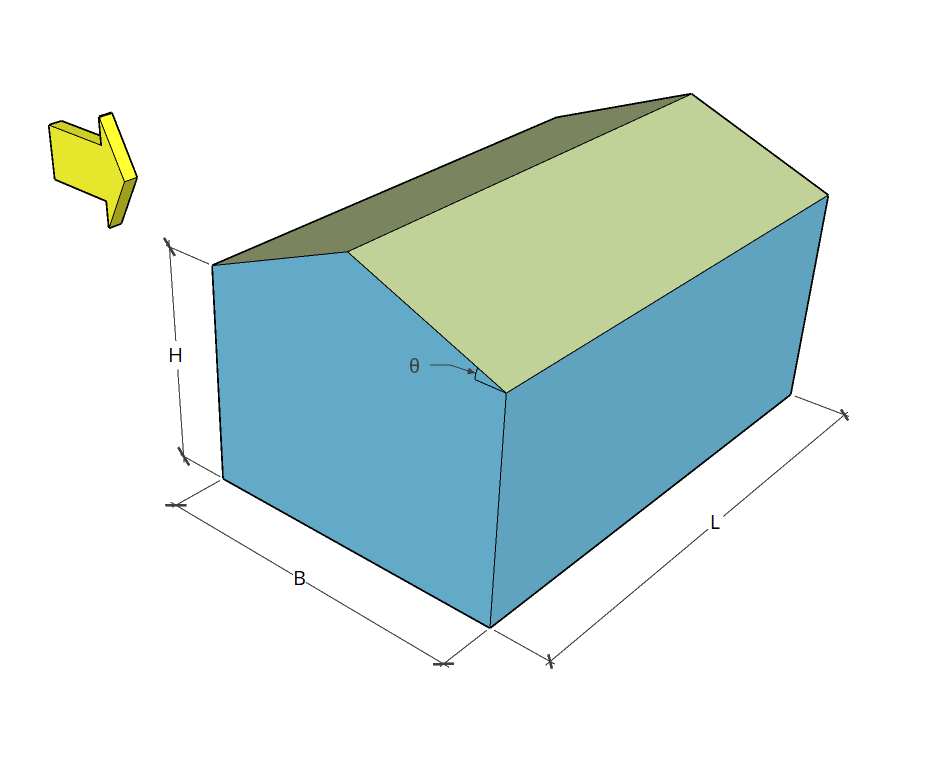
Dimensions	B = 4 m × L = 14 m in plan H = Eave height of 2.4 m Apex height at elev. 3.4 m Roof slope 1:2 (26.565°) No opening
Cladding	Purlins spaced at 0.745m Wall studs spaced at 0.8m

Using the IS 875-3: 2015, the design wind speed for the location and the design wind pressure for the rectangular building with pitched roof can be solved using the equations below:

Design wind speed at height z (in m/s): V_z = V_bk₁k₂k₃k₄ (1)

Where:
V_b is theBasic wind speed, m/s
k₁ is the Probability factor (risk coefficient) based on 6.3.1 of IS 875-3
k₂ is the Terrain roughness and height factor based on 6.3.2 of IS 875-3
k₃ is the Topography factor based on 6.3.3 of IS 875-3
k₄ is the Importance factor for the cyclonic region based on 6.3.4 of IS 875-3

Design wind pressure (in Pa): p_d = K_dK_aK_cp_z (2)

Where:
K_d is the Wind directionality factor based on 7.2.1 of IS 875-3. Equal to 1.0 when considering local pressure coefficients.
K_a is the Area averaging factor based on 7.2.2 of IS 875-3
K_c is the Combination factor based on 7.3.3.13 IS 875-3
p_z is equal to 0.60V_z² in Pa
Note that p_d should not be taken less than 0.70p_z

From the design pressure p_d obtained, the pressure will be distributed to the members of the by using:

Wind force on surface or members (in N): F = (C_pe – C_pi)Ap_d (3)

Where:
A is the surface area of the structural element or cladding unit
C_pe is the external pressure coefficients
C_pi is the internal pressure coefficients

We will dive deep into the details of each parameter below.

Basic Wind Speed V_b

From Figure 1 of IS 875-3, the site location is situation of the map where the basic wind speed V_b is equal to 39 m/s.

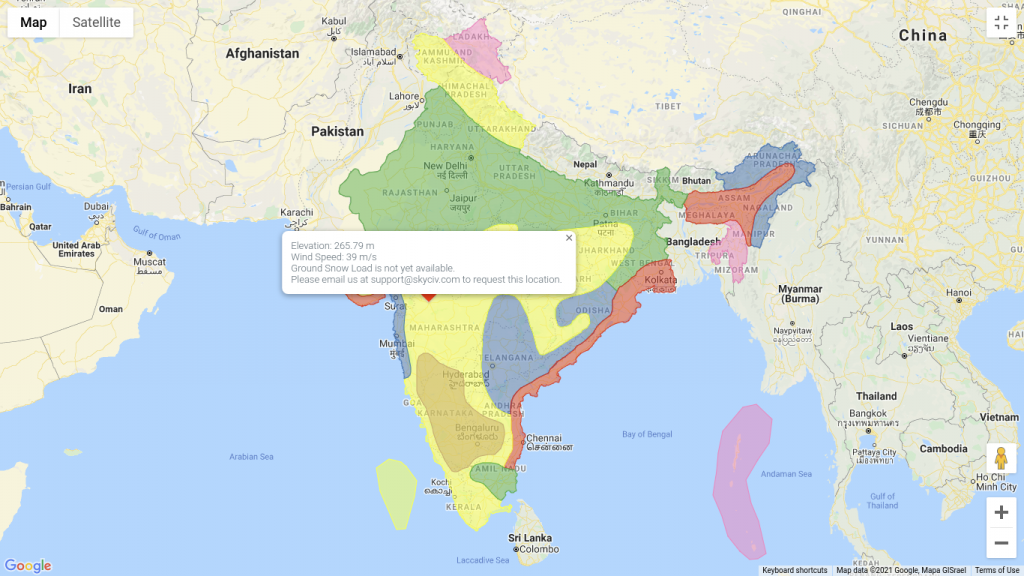
SkyCiv can automate the wind speed calculations just defining the site location in India. Try our SkyCiv Free Wind Tool.

Free Wind Load Calculator

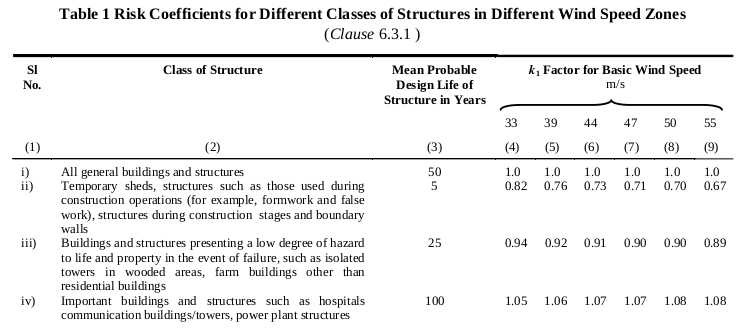
Probability Factor (Risk Coefficient) k₁

Table 1 of IS 875-3 presents the risk coefficients for different classes of structures in different wind speed zones. For this structure, since it is a barnhouse and will be used to shelter some livestock animals, the structure is classified under “Buildings and structures presenting a low degree of hazard to life and property in the event of failure, such as isolated towers in wooded areas, farm buildings other than residential buildings.” Hence, from Table 1 of IS 875-3, the corresponding probability factor (risk coefficient) k₁ is equal to 0.92.

Terrain Roughness and Height Factor k₂

For this structure, it is located at the center of a farm where there are no immediate obstructions. Hence, the terrain can be classified as Category 1. Using Table 2 of IS 875-3:2015, we can obtain k₂ values (which varies depending on the height being considered):

Height	k2
Reference height, H = 2.4 m	1.05

Topography Factor k₃

In order to account for topographic effects, we need to get the elevation data of the location for the eight (8) cardinal directions – N, S, W, E, NW, NE, SW, and SE – using Google elevation API. Based on the data, we can generally assume that the terrain is “Flat” for all directions. Hence, based on 6.3.3 of IS 875-3:2015, we can set our k₃ equal to 1.0.

Importance Factor k₄

Since the site location is not located within the east coast of India and the structure will only be used for agricultural purposes, the value of k₄ is equal to 1.0 based on 6.3.4 of IS 875-3:2015

Design Wind Speed V_z

From the factors above, we can already solve the design wind speed V_z using Equation (1):

Level	Vb m/s	k1	k2	k3	k4	Vz m/s
H = 2.4 m	39.0	0.92	1.05	1.0	1.0	37.674

From the design wind speed, we can calculate the design wind pressure p_d.

Wind Directionality Factor K_d

From 7.2.1 of IS 875-3:2015, the Wind Directionality Factor K_d is equal to 0.9 for frames and when considering local pressure coefficients, will be equal to 1.0. For this example, we will use K_d equal to 1.0 for purlins and wall studies and for K_d equal to 0.9 for the columns and trusses.

Area Averaging Factor K_a

The Area Averaging Factor K_a can be calculated using Table 4 of IS 875-3:2015:

K_a = 1.0 for area less than or equal to 10 sq.m.
K_a = 0.9 for area equal to 25 sq.m.
K_a = 0.8 for area greater than or equal to 100 sq.m.

Note that K_a can be linearly interpolated between values. For this structure, we need to get the tributary areas of columns for windward (Zone A), leeward (Zone B), sidewalls (Zone C and D), and truss for the roof. Moreover, we will also consider the tributary area of the wall studs and purlins.

Component	Area, sq.m.	Ka
Column	2.4×3.5 m = 8.4 sq.m.	1.0
Truss	4×3.5 m (projection) = 14 sq.m.	0.97
Wall studs	0.8×3.5 m = 2.8 sq.m.	1.0
Purlins	0.745×3.5 m = 2.608 sq.m.	1.0

Combination factor K_c

Since we will considered the simultaneous action of wall and roof pressures and internal pressures, the assumed Combination factor K_c is equal to 0.9 as referenced in 7.3.3.13 of IS 875-3:2015.

Design Wind Pressure, p_d

Using Equation (2), we can calculate the design wind pressure, p_d, Note that p_z = 851.598 Pa and p_d should not be less than 0.7p_z or 596.119Pa.

Component	Ka	Kd	Kc	pz	pd
Column	1.0	1.0	0.9	851.598	766.438
Truss	0.97	1.0	0.9	851.598	743.445
Wall studs	1.0	1.0	0.9	851.598	766.438
Purlins	1.0	1.0	0.9	851.598	766.438

From these data, we need to calculate the pressure coefficients in order to distribute the design pressure to the components.

Internal Pressure Coefficients C_pi

The internal pressure coefficients C_pi can be determined from 7.3.2 of IS 875-3:2015. For this structure, it is assumed the total opening on the wall is less than 5 percent of the total wall area. Therefore, the C_pi values for this example are +0.2 and -0.2.

External Pressure Coefficients C_pe

The External Pressure Coefficients C_pe depend on certain parameters such as height, width, length, roof angle, and roof profile.

Wall External Pressure Coefficients

The external pressure coefficients for walls depend on h/w and l/w ratio, where h is the eave height, w is the least dimension of the building, and l is the larger dimension of the building. For this example, h = H, l = L, and w = B. Therefore, h/w = 0.6 and l/w = 3.5. From Table 5 of IS 875-3:2015, the corresponding C_pe values are as follows:

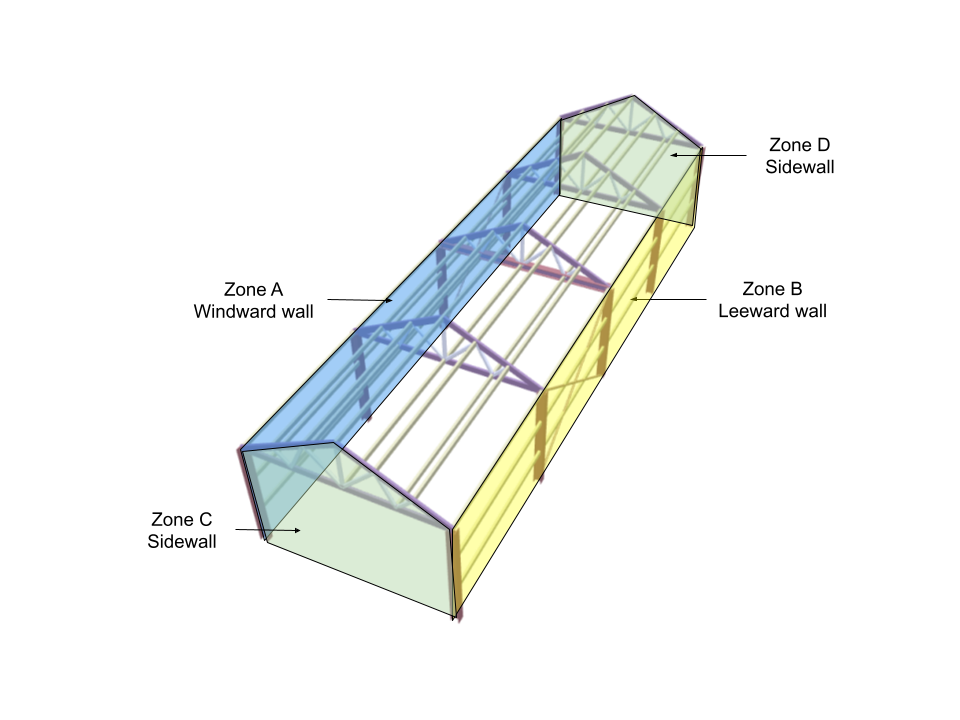
For wind angle = 0 degrees:

Zone/Surface	Cpe
Zone A – Windward wall	+0.7
Zone B – Leeward wall	-0.3
Zone C – Sidewall	-0.7
Zone D – Sidewall	-0.7
Local zone (0.25w from edge)	-1.1

For wind angle = 90 degrees:

Zone/Surface	Cpe
Zone A – Windward wall	-0.5
Zone B – Leeward wall	-0.5
Zone C – Sidewall	+0.7
Zone D – Sidewall	-0.1
Local zone (0.25w from edge)	-1.1

Note that w = 4 m.

Roof External Pressure Coefficients

For this structure, since the roof profile is gable or duopitch, the roof external pressure coefficients will be calculated based on Table 6 of IS 875-3:2015. For this example since h/w = 0.6, and the roof angle is 26.565°, the C_pe values will be interpolated using the following values:

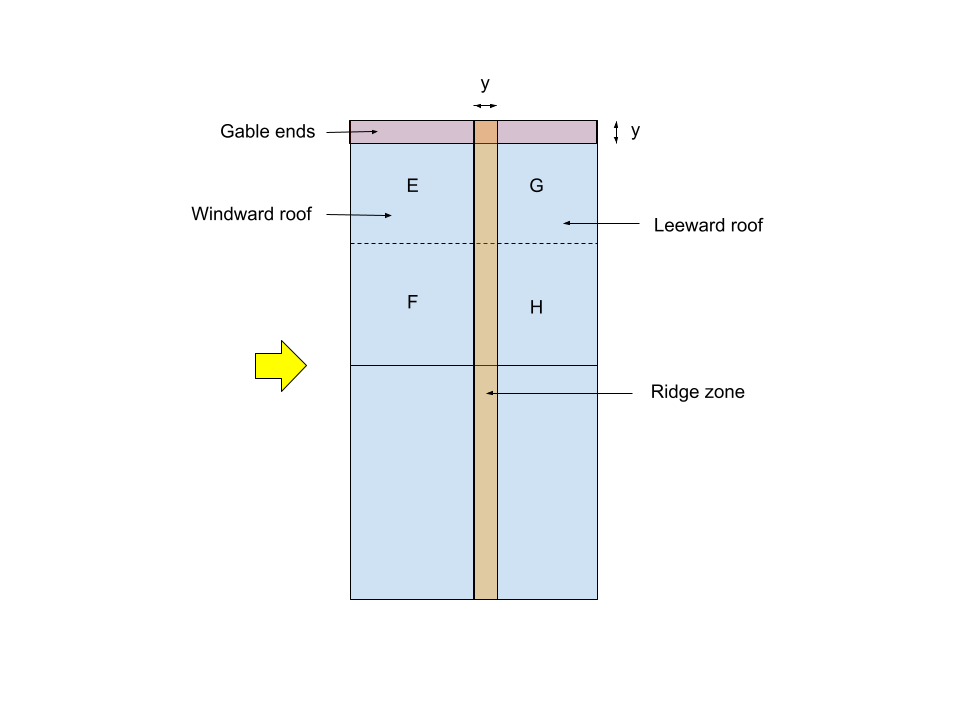
Note: y = 0.15w = 0.6m

For wind angle = 0 degrees:

Roof angle	Zone EF – Windward	Zone GH – Leeward
20°	-0.7	-0.5
26.565°	-0.109	-0.5
30°	-0.2	-0.5

For wind angle = 90 degrees:

Roof angle	Zone EG – Crosswind	Zone FH – Crosswind
20°	-0.8	-0.6
26.565°	-0.8	-0.6
30°	-0.8	-0.6

For local pressures:

Roof angle	Gable ends	Ridge zones
20°	-1.5	-1.0
26.565°	-1.172	-1.0
30°	-1.0	-1.0

The final roof pressure coefficients will be:

Zone/Surface	Wind direction – 0 degrees	Wind direction – 90 degrees
Zone EF – Windward	-0.109	–
Zone GH – Leeward	-0.5	–
Zone EG – Crosswind	–	-0.8
Zone FH – Crosswind	–	-0.6
Gable ends	-1.172	-1.172
Ridge zones	-1.0	-1.0

Combined internal and external pressures

From the values above, the wind force can be calculated using Equation (3). However, for simplicity, we will just be getting the design pressure (not multiplying the values to the area A) and also will be considering the wind direction angle 0 degrees for the main frame (column and truss). The frame spacing is equal to 3.5m. Note that p_d = 766.438 Pa for both column and wall studs.

For columns and wall studs – 0 degrees:

Zone/Surface	Cpe	Cpi	Cpe–Cpi	p = pd(Cpe-Cpi) Pa	For Column px3.5m N/m	For wall studs px0.8m N/m
Zone A – Windward wall	0.7	+0.2 -0.2	+0.5 +0.9	383.219 689.795	1341.267 2414.281	306.575 551.836
Zone B – Leeward wall	-0.3	+0.2 -0.2	-0.5 -0.1	-383.219 -76.644	-1341.267 -268.253	-306.575 -61.315
Local zone (1m from edge)	-1.1	+0.2 -0.2	-1.3 -0.9	-996.370 -689.795	-3487.295 -2414.281	-797.096 -551.836

The pressures on the columns will be multiplied to 3.5m in order to get a uniform load. Moreover, for the wall studs, it will be multiplied with 0.8m. Note that a positive pressure means it is acting towards the surface and negative is acting away from the surface (suction).

For truss and purlins – 0 degress:

Zone/Surface	Cpe	Cpi	Cpe–Cpi	p = pd(Cpe-Cpi) Pa	Truss px3.5m N/m	Purlins px0.745m N/m
Zone EF – Windward	-0.109	+0.2 -0.2	-0.309 +0.091	-229.725 67.654	-804.036 236.787	-171.145 50.402
Zone GH – Leeward	-0.5	+0.2 -0.2	-0.7 -0.3	-520.412 -223.034	-1821.441 -780.617	-387.707 -166.160
Gable ends	-1.172	+0.2 -0.2	-1.372 -0.972	-1051.553 -744.978	-3680.437 -2607.423	–
Ridge zones	-1.0	+0.2 -0.2	-1.2 -0.8	-919.726 -613.151	-3219.041 -2146.027	–

The pressures on the truss will be multiplied to 3.5m in order to get a uniform load. Moreover, for the wall studs, it will be multiplied with 0.745m. Note that p_d = 766.438 Pa for the purlins and p_d = 743.445 Pa for the truss.

Considering one critical frame – spacing is 3.5m:

For p_d(C_pe – +C_pi):

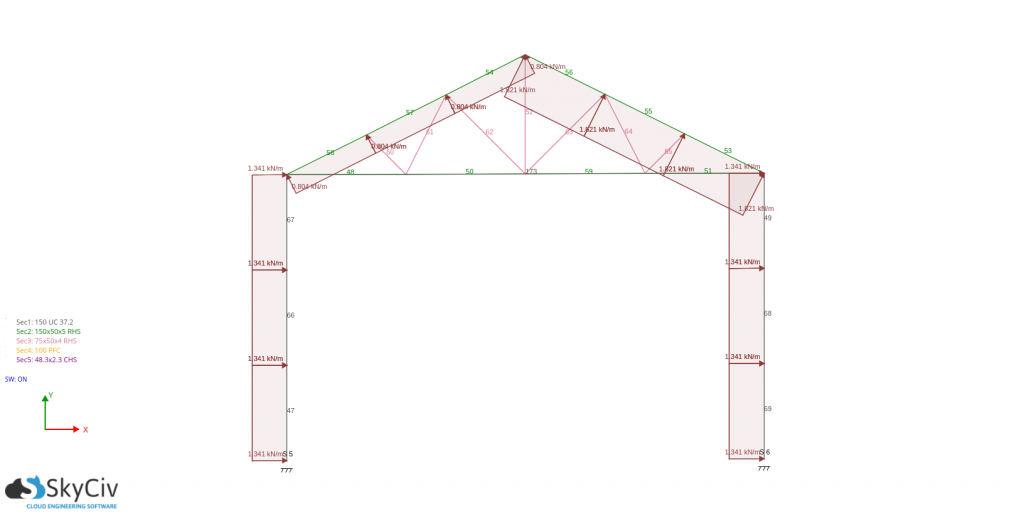
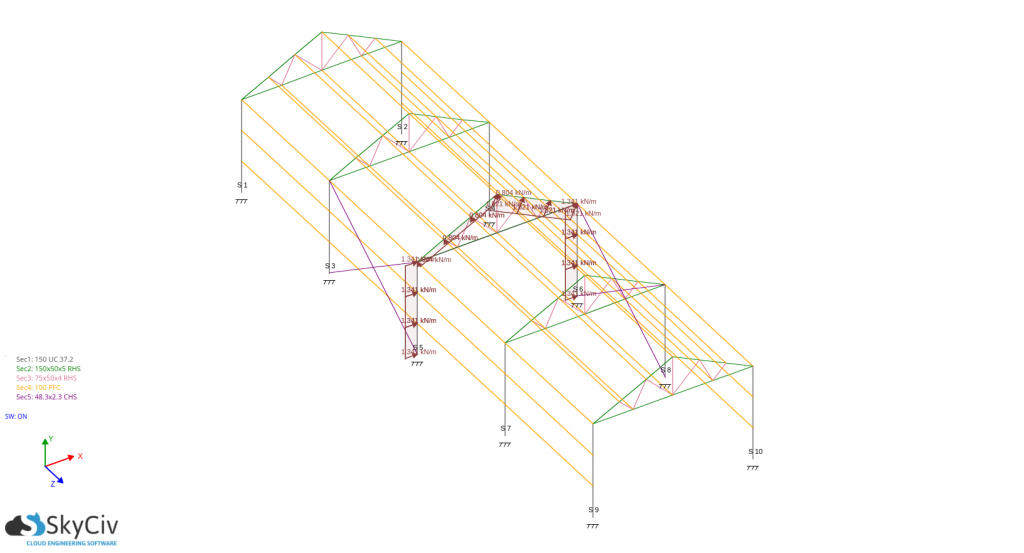
For p_d(C_pe – -C_pi):

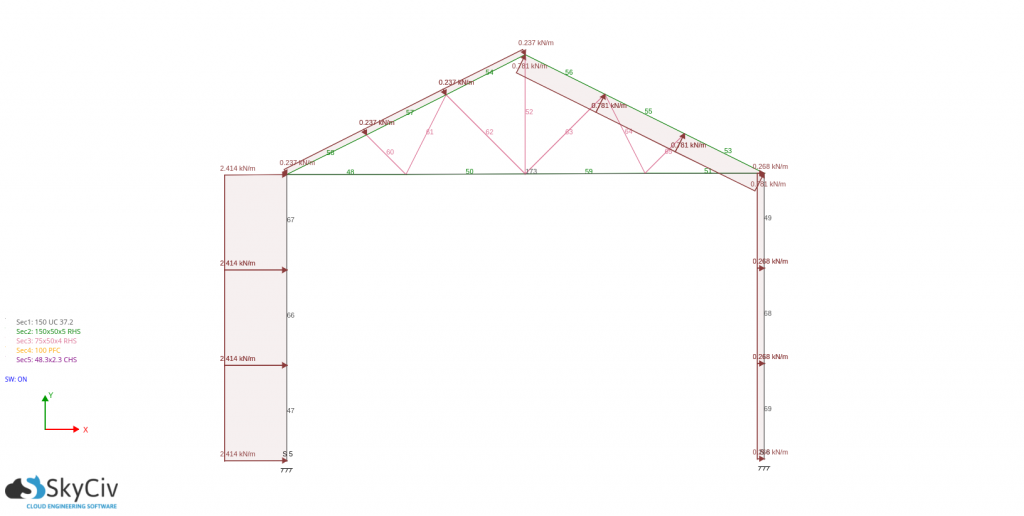
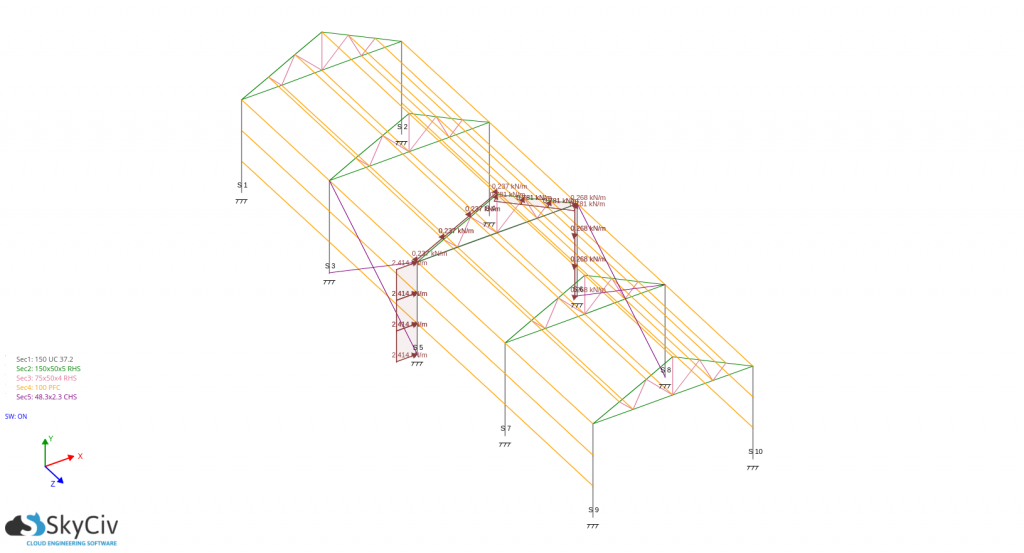
For the design of wall studs and purlins, you just need to get the absolute maximum pressure acting on it and use it as the basis in calculating the design forces. For this case, the design wind load are: -797.096 N/m for wall stud and -783.407N/m for the purlins,

These calculations can be all be performed using SkyCiv’s Load Generator Software for IS 875-3 and other codes as well. Users can enter in a site location to get wind speeds and topography factors, enter in building parameters and generate the wind pressures. Try our SkyCiv Free Wind Tool for wind speed and wind pressure calculations on gable structures.

Skyciv Wind Load Calculator

References:

• Design Loads (Other than Earthquake) for Buildings and Structures — Code of Practice (Part 3 Wind Loads ed.). (2015). Bureau of Indian Standards.