Base Plate Design Example using AISC 360-22 and ACI 318-19
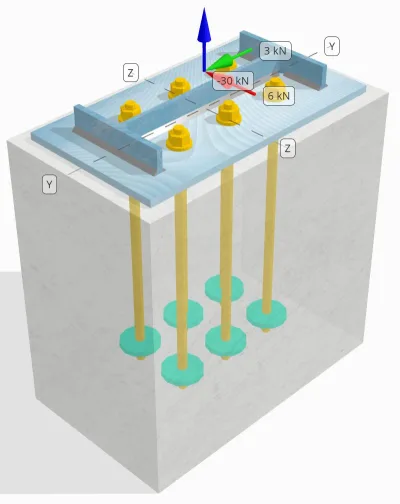
Problem Statement:
Determine whether the designed column-to-base plate connection is sufficient for 30 kN tension load, 3 kN Vy shear load, and 6 kN Vz shear load.
Given Data:
Column:
Column section: W14x30
Column area: 5709.7 mm2
Column material: A992
Base Plate:
Base plate dimensions: 12 in x 12 in
Base plate thickness: 1/2 in
Base plate material: A36
Grout:
Grout Thickness: 0 mm
Concrete:
Concrete dimensions: 300 mm x 500 mm
Concrete thickness: 500 mm
Concrete material: 20.7 MPa
Cracked or Uncracked: Cracked
Anchors:
Anchor diameter: 16 mm
Effective embedment length: 400 mm
Anchor Ending: Circular Plate
Embedded plate diameter: 70 mm
Embedded plate thickness: 10 mm
Steel Material: A325N
Threads in Shear Plane: Included
Welds:
Weld size: 1/4 in
Filler metal classification: E70XX
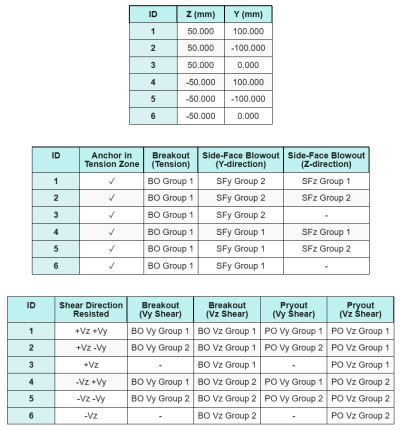
Anchor Data (from SkyCiv Calculator):
Note:
The purpose of this design example is to demonstrate the step-by-step calculations for capacity checks involving concurrent shear and axial loads. Some of the required checks have already been discussed in the previous design examples. Please refer to the links provided in each section.
Step-by-Step Calculations:
Check #1: Calculate weld capacity
To determine the weld capacity under simultaneous loading, we first need to calculate the weld demand due to the shear load and the weld demand due to the tension load. You may refer to this link for the procedure to obtain the weld demands for shear, and this link for the tension weld demands.
For this design, the weld demand at the web due to the tension load is found to be as follows, where the stress is expressed as force per unit length.
\(r_{u,\text{web}} = \frac{T_{u,\text{anchor}}}{l_{\text{eff}}} = \frac{5\ \text{kN}}{93.142\ \text{mm}} = 0.053681\ \text{kN/mm}\)
Furthermore, the weld stress at any part of the column section due to the shear load is determined as:
\(v_{uy} = \frac{V_y}{L_{\text{weld}}} = \frac{3\ \text{kN}}{1250.7\ \text{mm}} = 0.0023987\ \text{kN/mm}\)
\(v_{uz} = \frac{V_z}{L_{\text{weld}}} = \frac{6\ \text{kN}}{1250.7\ \text{mm}} = 0.0047973\ \text{kN/mm}\)
Since there is a combination of tension and shear loads at the web, we need to obtain the resultant. Expressing this as force per unit length, we have:
\(r_u = \sqrt{(r_{u,\text{web}})^2 + (v_{uy})^2 + (v_{uz})^2}\)
\(r_u = \sqrt{(0.053681\ \text{kN/mm})^2 + (0.0023987\ \text{kN/mm})^2 + (0.0047973\ \text{kN/mm})^2}\)
\(r_u = 0.053949\ \text{kN/mm}\)
For the flanges, only shear stresses are present. Thus, the resultant is:
\(r_u = \sqrt{(v_{uy})^2 + (v_{uz})^2}\)
\(r_u = \sqrt{(0.0023987\ \text{kN/mm})^2 + (0.0047973\ \text{kN/mm})^2} = 0.0053636\ \text{kN/mm}\)
Next, we calculate the weld capacities. For the flange, we determine the angle θ using the Vz and Vy loads.
\( \theta = \tan^{-1}\!\left(\frac{v_{uy}}{v_{uz}}\right) = \tan^{-1}\!\left(\frac{0.0023987\ \text{kN/mm}}{0.0047973\ \text{kN/mm}}\right) = 0.46365\ \text{rad} \)
Consequently, the kds factor and weld capacity are calculated using AISC 360-22 Eq. J2-5 and Eq. J2-4.
\(k_{ds} = 1.0 + 0.5(\sin(\theta))^{1.5} = 1 + 0.5 \times (\sin(0.46365\ \text{rad}))^{1.5} = 1.1495\)
\(\phi r_{n,flg} = \phi\,0.6\,F_{exx}\,E_w\,k_{ds} = 0.75 \times 0.6 \times 480\ \text{MPa} \times 4.95\ \text{mm} \times 1.1495 = 1.2291\ \text{kN/mm}\)
For the web, we calculate the angle θ using a different formula. Note that Vuy is used in the formula since it represents the load parallel to the weld axis.
\( \theta = \cos^{-1}\!\left(\frac{v_{uy}}{r_u}\right) = \cos^{-1}\!\left(\frac{0.0023987\ \text{kN/mm}}{0.053949\ \text{kN/mm}}\right) = 1.5263\ \text{rad} \)
Using AISC 360-22 Eq. J2-5 and Eq. J2-4, the kds factor and the resulting weld capacity are determined in the same manner.
\(k_{ds} = 1.0 + 0.5(\sin(\theta))^{1.5} = 1 + 0.5 \times (\sin(1.5263\ \text{rad}))^{1.5} = 1.4993\)
\(\phi r_{n,web} = \phi\,0.6\,F_{exx}\,E_w\,k_{ds} = 0.75 \times 0.6 \times 480\ \text{MPa} \times 4.95\ \text{mm} \times 1.4993 = 1.603\ \text{kN/mm}\)
Lastly, we perform base metal checks for both the column and the base plate, then obtain the governing base metal capacity.
\( \phi r_{nbm,col} = \phi\,0.6\,F_{u,col}\,t_{col,half} = 0.75 \times 0.6 \times 448.2\ \text{MPa} \times 3.429\ \text{mm} = 0.6916\ \text{kN/mm} \)
\( \phi r_{nbm,bp} = \phi\,0.6\,F_{u,bp}\,t_{bp} = 0.75 \times 0.6 \times 400\ \text{MPa} \times 12\ \text{mm} = 2.1595\ \text{kN/mm} \)
\( \phi r_{nbm} = \min\big(\phi r_{nbm,bp},\ \phi r_{nbm,col}\big) = \min(2.1595\ \text{kN/mm},\ 0.6916\ \text{kN/mm}) = 0.6916\ \text{kN/mm} \)
We then compare the fillet weld capacities and base metal capacities for the weld demands at the flanges and web separately.
Since 0.053949 kN/mm < 0.6916 kN/mm, the weld capacity is sufficient.
Check #2: Calculate base plate flexural yielding capacity due to tension load
A design example for the base plate flexural yielding capacity is already discussed in the Base Plate Design Example for Tension. Please refer to this link for the step-by-step calculation.
Check #3: Calculate anchor rod tensile capacity
A design example for the anchor rod tensile capacity is already discussed in the Base Plate Design Example for Tension. Please refer to this link for the step-by-step calculation. Please refer to this link for the step-by-step calculation.
Check #4: Calculate concrete breakout capacity in tension
A design example for the capacity of the concrete in tension breakout is already discussed in the Base Plate Design Example for Tension. Please refer to this link for the step-by-step calculation. Please refer to this link for the step-by-step calculation.
Check #5: Calculate anchor pullout capacity
A design example for the anchor pull out capacity is already discussed in the Base Plate Design Example for Tension. Please refer to this link for the step-by-step calculation. Please refer to this link for the step-by-step calculation.
Check #6: Calculate embed plate flexural capacity
A design example for the supplementary check on the embedded plate flexural yielding capacity is already discussed in the Base Plate Design Example for Tension. Please refer to this link for the step-by-step calculation.
Check #7: Calculate side-face blowout capacity in Y-direction
To calculate the Side-Face Blowout (SFBO) capacity, we first determine the total tension force on the anchors closest to the edge. For this check, we will evaluate the capacity of the edge along the Y-direction.
Since the failure cone projections of the SFBO along the Y-direction overlap, the anchors are treated as an anchor group.
The total tension demand of the anchor group is calculated as:
\(N_{ua} = \left(\frac{N_x}{n_{a,t}}\right) n_{y,g1} = \left(\frac{30\ \text{kN}}{6}\right) \times 3 = 15\ \text{kN}\)
Next, we determine the edge distances:
\(c_{z,\min} = \min(c_{\text{left},g1},\ c_{\text{right},g1}) = \min(100\ \text{mm},\ 200\ \text{mm}) = 100\ \text{mm}\)
\(c_{y,\min} = \min(c_{\text{top},g1},\ c_{\text{bottom},g1}) = \min(150\ \text{mm},\ 150\ \text{mm}) = 150\ \text{mm}\)
Using these edge distances, we calculate the anchor group capacity in accordance with ACI 318-19 Eq. (17.6.4.1).
\(N_{sbg} = \left(\frac{1 + \dfrac{c_{y,\min}}{c_{z,\min}}}{4} + \frac{s_{sum,y,g1}}{6\,c_{z,\min}}\right)\times 13 \times \left(\frac{c_{z,\min}}{1\ \text{mm}}\right)\times \sqrt{\frac{A_{brg}}{\text{mm}^2}}\ \lambda_a \sqrt{\frac{f_c}{\text{MPa}}}\times 0.001\ \text{kN}\)
\(N_{sbg} = \left(\frac{1 + \dfrac{150\ \text{mm}}{100\ \text{mm}}}{4} + \frac{200\ \text{mm}}{6\times 100\ \text{mm}}\right)\times 13 \times \left(\frac{100\ \text{mm}}{1\ \text{mm}}\right)\times \sqrt{\frac{3647.4\ \text{mm}^2}{1\ \text{mm}^2}}\times 1 \times \sqrt{\frac{20.68\ \text{MPa}}{1\ \text{MPa}}}\times 0.001\ \text{kN}\)
\(N_{sbg} = 342.16\ \text{kN}\)
In the original equation, a reduction factor is applied when the anchor spacing is less than 6ca₁, assuming the headed anchors have sufficient edge distance. However, in this design example, since ca₂ < 3ca₁, the SkyCiv calculator applies an additional reduction factor to account for the reduced edge capacity.
Finally, the design SFBO capacity is:
\(\phi N_{sbg} = \phi\,N_{sbg} = 0.7 \times 342.16\ \text{kN} = 239.51\ \text{kN}\)
Since 15 kN < 239.51 kN, the SFBO capacity along the Y-direction is sufficient.
Check #8: Calculate side-face blowout capacity in Z-direction
Following the same approach as in Check #7, the total tension demand of the anchor group for the anchors closest to the Z-direction edge is:
\(N_{ua} = \left(\frac{N_x}{n_{a,t}}\right)n_{z,g1} = \left(\frac{30\ \text{kN}}{6}\right)\times 2 = 10\ \text{kN}\)
The edge distances are calculated as:
\(c_{y,\min} = \min(c_{\text{top},g1},\ c_{\text{bottom},g1}) = \min(150\ \text{mm},\ 350\ \text{mm}) = 150\ \text{mm}\)
\(c_{z,\min} = \min(c_{\text{left},g1},\ c_{\text{right},g1}) = \min(100\ \text{mm},\ 100\ \text{mm}) = 100\ \text{mm}\)
The nominal SFBO capacity is then determined as:
\(N_{sbg} = \left(\frac{1 + \dfrac{c_{z,\min}}{c_{y,\min}}}{4} + \frac{s_{sum,z,g1}}{6\,c_{y,\min}}\right)\times 13 \times \left(\frac{c_{y,\min}}{1\ \text{mm}}\right)\times \sqrt{\frac{A_{brg}}{\text{mm}^2}}\ \lambda_a \sqrt{\frac{f_c}{\text{MPa}}}\times 0.001\ \text{kN}\)
\(N_{sbg} = \left(\frac{1 + \dfrac{100\ \text{mm}}{150\ \text{mm}}}{4} + \frac{100\ \text{mm}}{6\times 150\ \text{mm}}\right)\times 13 \times \left(\frac{150\ \text{mm}}{1\ \text{mm}}\right)\times \sqrt{\frac{3647.4\ \text{mm}^2}{1\ \text{mm}^2}}\times 1 \times \sqrt{\frac{20.68\ \text{MPa}}{1\ \text{MPa}}}\times 0.001\ \text{kN}\)
\(N_{sbg} = 282.65\ \text{kN}\)
Since the edge distance ca₂ is still less than 3ca₁, the same modified reduction factor is applied.
Finally, the design SFBO capacity is:
\(\phi N_{sbg} = \phi\,N_{sbg} = 0.7 \times 282.65\ \text{kN} = 197.86\ \text{kN}\)
Since 10 kN < 197.86 kN, the SFBO capacity along the Z-direction is sufficient.
Check #9: Calculate breakout capacity (Vy shear)
A design example for the concrete breakout capacity in Vy shear is already discussed in the Base Plate Design Example for Shear. Please refer to this link for the step-by-step calculation.
Check #10: Calculate breakout capacity (Vz shear)
A design example for the concrete breakout capacity in Vy shear is already discussed in the Base Plate Design Example for Shear. Please refer to this link for the step-by-step calculation.
Check #11: Calculate pryout capacity (Vy shear)
A design example for the capacity of the concrete against pryout failure due to Vy shear is already discussed in the Base Plate Design Example for Shear. Please refer to this link for the step-by-step calculation.
Check #12: Calculate pryout capacity (Vz shear)
A design example for the capacity of the concrete against pryout failure due to Vy shear is already discussed in the Base Plate Design Example for Shear. Please refer to this link for the step-by-step calculation.
Check #13: Calculate anchor rod shear capacity
A design example for the anchor rod shear capacity is already discussed in the Base Plate Design Example for Shear. Please refer to this link for the step-by-step calculation.
Check #14: Calculate anchor rod shear and axial capacity (AISC)
To determine the capacity of the anchor rod under combined shear and axial loads, we use AISC 360-22 Eq. J3-3a. In this calculator, the equation is rearranged to express the result as the modified shear strength instead.
The shear demand is defined as the shear load per anchor.
\(V_{ua} = V_{ua} = 2.5\ \text{kN}\)
The tension demand is expressed as the tensile stress in the anchor rod.
\(f_{ut} = \frac{N_{ua}}{A_{rod}} = \frac{5\ \text{kN}}{201.06\ \text{mm}^2} = 24.868\ \text{MPa}\)
The modified shear capacity of the anchor rod is then calculated as:
\(F’_{nv} = \min\!\left(1.3\,F_{nv} – \left(\frac{F_{nv}}{\phi F_{nt}}\right) f_{ut},\; F_{nv}\right)\)
\(F’_{nv} = \min\!\left(1.3\times 232.69\ \text{MPa} – \left(\frac{232.69\ \text{MPa}}{0.75\times 387.82\ \text{MPa}}\right)\times 24.868\ \text{MPa},\; 232.69\ \text{MPa}\right) = 232.69\ \text{MPa}\)
We then multiply this strength by the anchor area using AISC 360-22 Eq. J3-2.
\(\phi R_{n,\text{aisc}} = \phi F’_{nv} A_{\text{rod}} = 0.75 \times 232.69\ \text{MPa} \times 201.06\ \text{mm}^2 = 35.09\ \text{kN}\)
Since 2.5 kN < 35.09 kN, the anchor rod capacity is sufficient.
Check #15: Calculate interaction checks (ACI)
When checking the anchor rod capacity under combined shear and tension loads using ACI, a different approach is applied. For completeness, we also perform the ACI interaction checks in this calculation, which include other concrete interaction checks as well.
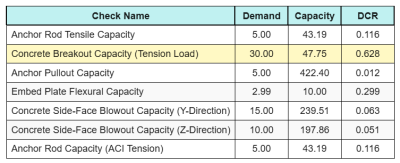
Here are the resulting ratios for all ACI tension checks:
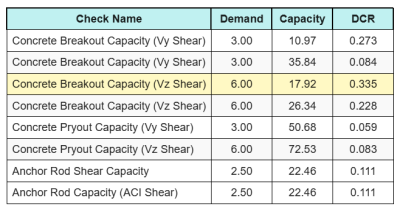
And here are the resulting ratios for all ACI shear checks:
We get the check with the largest ratio and compare it to the maximum interaction ratio using ACI 318-19 Eq. 17.8.3.
\(I_{int} = \frac{N_{ua}}{\phi N_n} + \frac{V_{ua}}{\phi V_n} = \frac{30}{47.749} + \frac{6}{17.921} = 0.96308\)
Since 0.96 < 1.2, the interaction check is sufficient.
Design Summary
The SkyCiv Base Plate Design software can automatically generate a step-by-step calculation report for this design example. It also provides a summary of the checks performed and their resulting ratios, making the information easy to understand at a glance. Below is a sample summary table, which is included in the report.
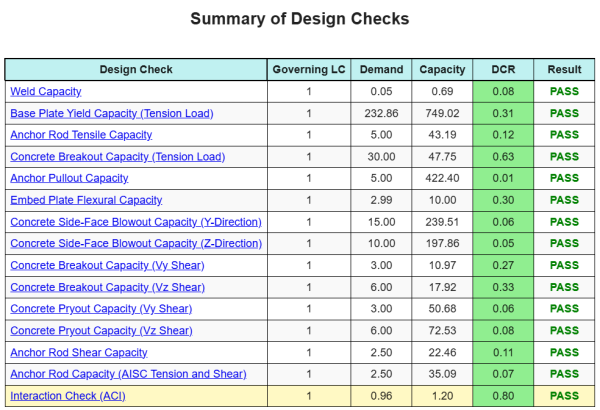
SkyCiv Sample Report
Click here to download a sample report.
Purchase Base Plate Software
Purchase the full version of the base plate design module on its own without any other SkyCiv modules. This gives you a full set of results for Base Plate Design, including detailed reports and more functionality.
