Tutorial: How to Solve a Truss Structure using Method of Sections
In this tutorial, we will explore and learn the benefits of using the Method of Sections to solve your truss structure. What are trusses? If you’re unsure about this, visit our What is a truss article. The method of sections is used to solve larger truss structures in a fast, simple manner. It involves taking a ‘cut’ through a number of members to evaluate their axial forces and use this as our basis to solve the rest of the truss structure.
The great thing is, SkyCiv Truss does this automatically for you. Model your own trusses and the software will show interactive step-by-step working out of the method of sections!
 Watch the Video Tutorial
Watch the Video Tutorial
Sample Question
For our worked example, we’ll be looking at the following question:
Question: Using the method of sections, determine the forces in members 10, 11, and 13 of the following truss structure:
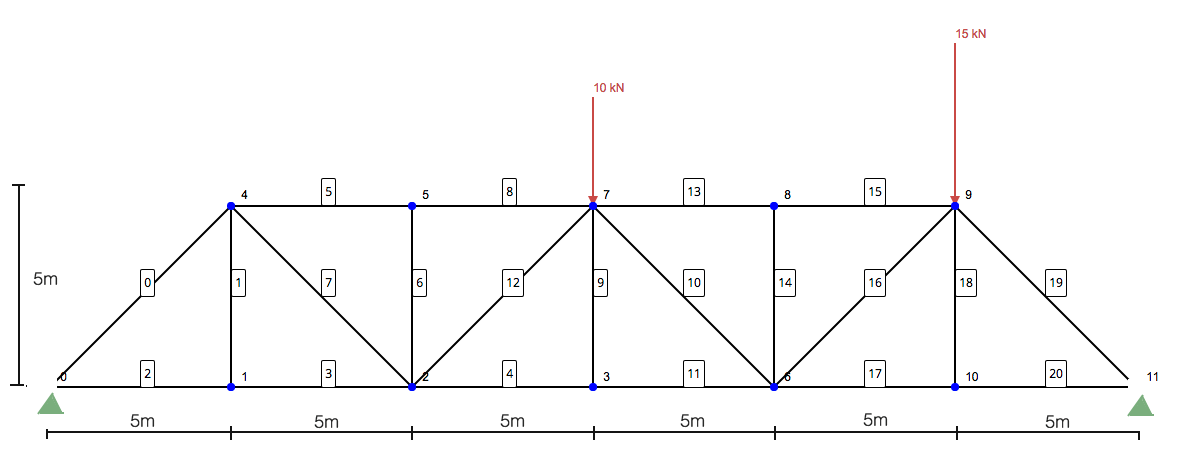
Step 1: Calculate the Reactions to the Supports
Like most static structural analyses, we must first start by locating and solving the reactions at supports. This will give us the boundary conditions we need to progress in solving the truss structure. Simplifying the structure to just include the loads and supports:
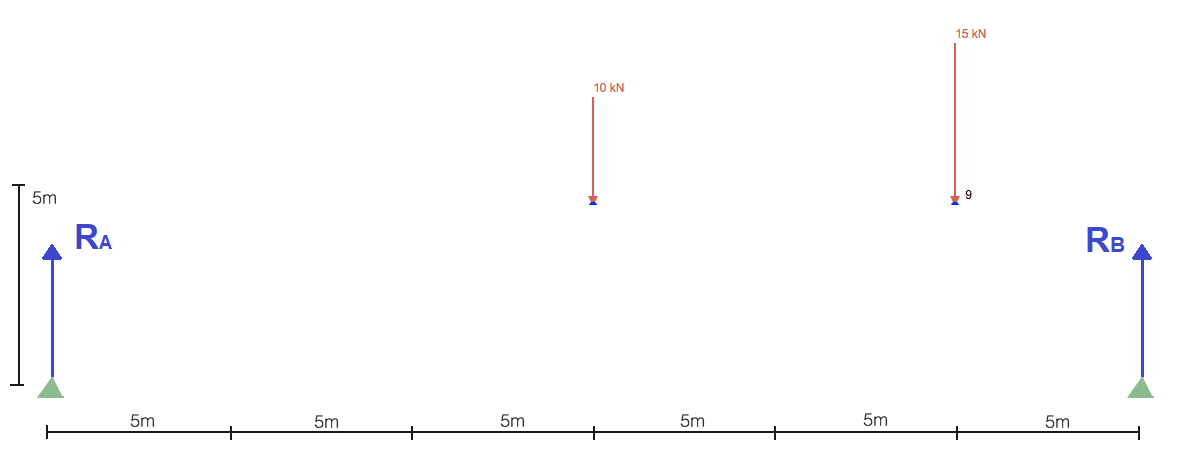
Without spending too much time calculating the reactions, you generally start by taking the sum of moments about a point. Taking the sum of moments about the left support gets us:

So the reaction at the right support (RB) is 17.5 kN in an upward direction. Now, taking the sum of forces in the y gives us the reaction RA as 7.5kN in an upward direction:

Step 2: Make a cut along the members of interest
Here comes the most important part of solving a truss using the method of sections. It involves making a slice through the members you wish to solve. This method of structural analysis is extremely useful when trying to solve some of the members without having to solve the entire structure using the method of joints. So, in our example here would be our slice:
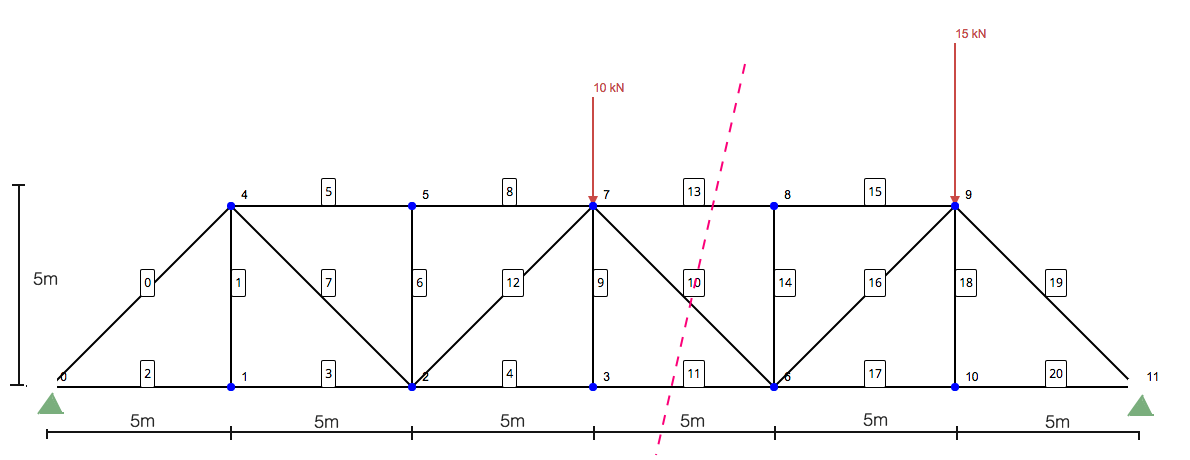
Focussing on the left side only, you are left with the following structure:
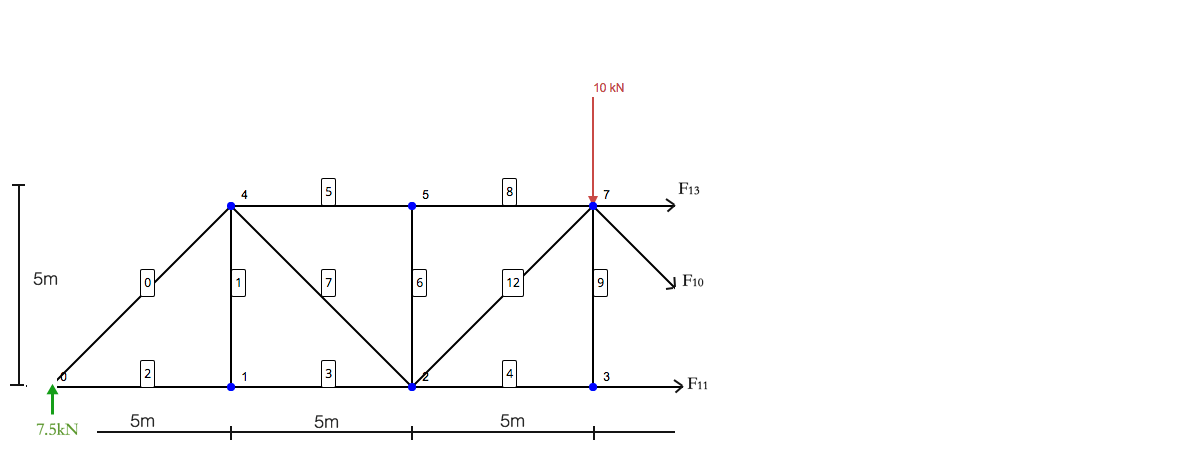
Now think of this structure as a single-standing structure. The laws of statics still apply – so the sum of moments and forces must all equal zero. The members with arrows (F13, F10, F11) are what stabilize the reaction and forces applied to the structure. Note that the sum of moments is taken about node 7 – as would exclude the forces of members 13 and 10 – leaving F11 to be isolated.
Using the above Free Body Diagram, we can obtain the following formulae:
Sum of forces in the y-direction:
[math]
\begin{align}
+\uparrow \text{ } \sum{F_y} &= 0\\
7.5\text{ kN} – 10 \text{ kN} – F_{10}sin(45^{\circ}) &= 0\\
F_{10} &= -3.536 \text{ kN}
\end{align}
[math]
Sum of moments about node 7:
[math]
\begin{align}
+\circlearrowleft \text{ } \sum{M_7} &= 0\\
-(15 \text{ m})(7.5 \text{ kN}) + (5 \text{ m})F_{11} &= 0\\
F_{11} &= 22.5 \text{ kN}
\end{align}
[math]
Sum of forces in the x-direction:
[math]
\begin{align}
+\rightarrow \text{ } \sum{F_x} &= 0\\
F_{13} + F_{11} + F_{10}cos(45^{\circ}) &= 0\\
F_{13} &= -F_{11} – F_{10}cos(45^{\circ}) \\
F_{13} &= – (22.5 \text{ kN}) – (-3.536 \text{ kN})cos(45^{\circ}) \\
F_{13} &= -22.5 \text{ kN} + (3.536 \text{ kN})cos(45^{\circ}) \\
F_{13} &= -20 \text{ kN}
\end{align}
[math]
Final Solution
We can use these results to solve the remaining members in the truss structure. We hope this truss calculation example has been useful and feel free to comment with your questions below. As a reference, the results for the entire Truss structure can be found below (using our Truss Calculator) which is great for checking your answers!

Summary of Steps
- Always Start by calculating reactions at supports
- Make a slice through the members you wish to solve
- Treat the half structure as its own static truss
- Solve the truss by taking the sum of forces = 0
- Take the moment about a node of more than one unknown member
SkyCiv Truss Software
We hope that you found this tutorial useful for your projects. Visit our truss tutorials for more useful information about truss and don’t forget to check out our guide to solving truss by Method of Joints.
SkyCiv Truss can calculate the method of sections automatically for you. Or try our Free Truss Calculator which will give you the final answer (no hand calculations).
To explore more functionality of SkyCiv software, sign up today to get started!

 Watch the Video Tutorial
Watch the Video Tutorial
