How to Calculate Axial Forces of A Truss System using Method of Joints?
In this tutorial, we will explain how to use the method of joints to calculate the internal member forces in a truss system or structure.
These forces are known as Axial Forces and are very important in truss analysis. If you’re unclear about what a truss is seen in our article – What is a Truss. The Method of Joints basically involves looking at each of the ‘joints’ (where the members meet) and applying static equations to solve.
The great thing is, SkyCiv Truss does this automatically for you. Model your own trusses and the software will show interactive step by step working out of the method of joints!

Step 1: Calculate the Reactions at the Supports
First, we calculate the reactions at the supports. We will start by looking at a simple example of a 5 member truss system:
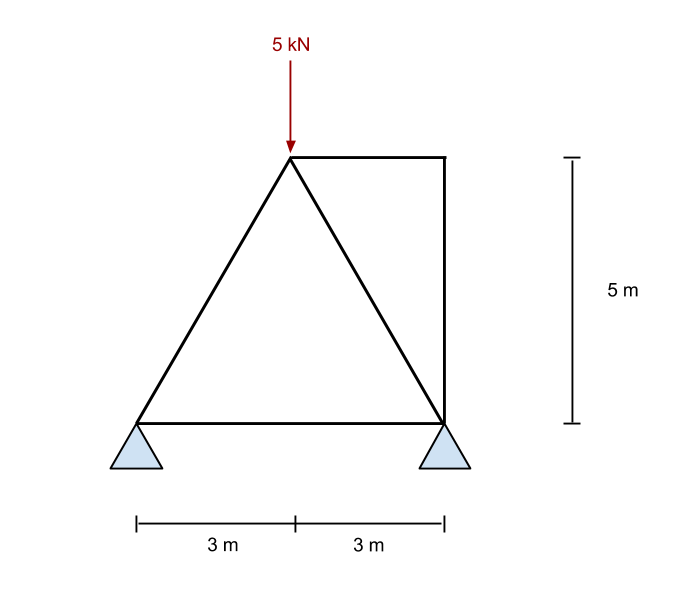
To calculate the bending moment in this truss system, we first take the sum of moments at the left reaction to be zero. We do this by ignoring all the members and just looking at the forces and supports in the structure. This is the same as the method used in the Bending Moment Reactions in our previous tutorial.
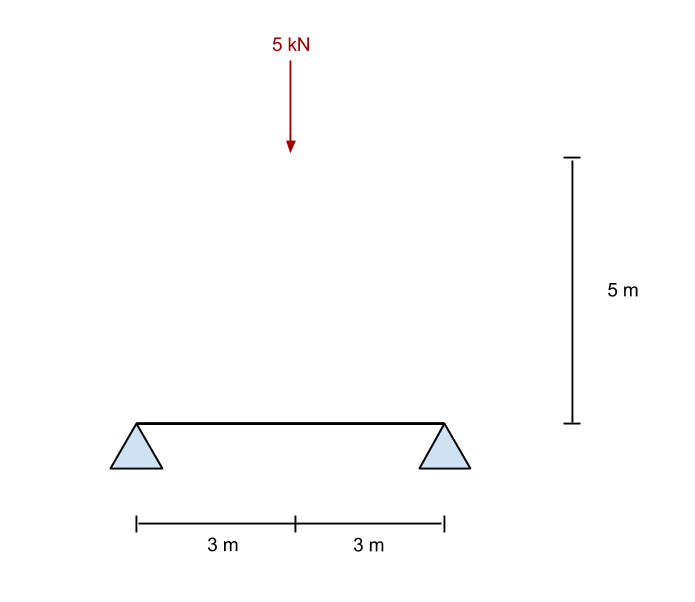
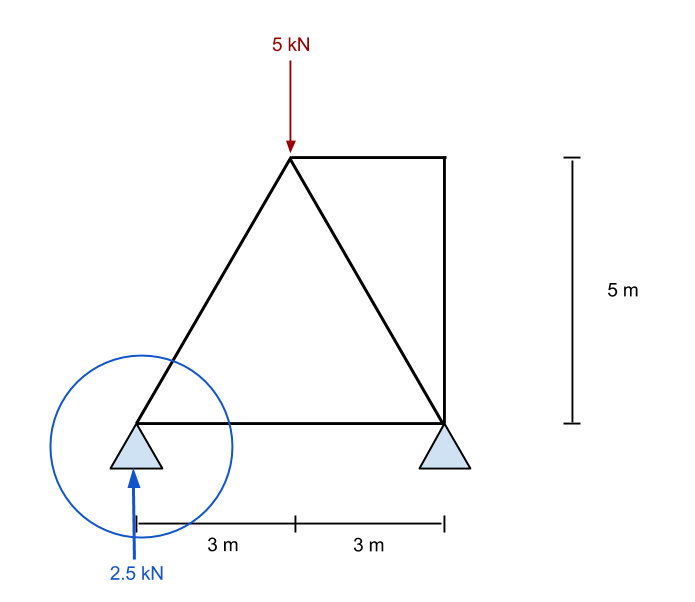
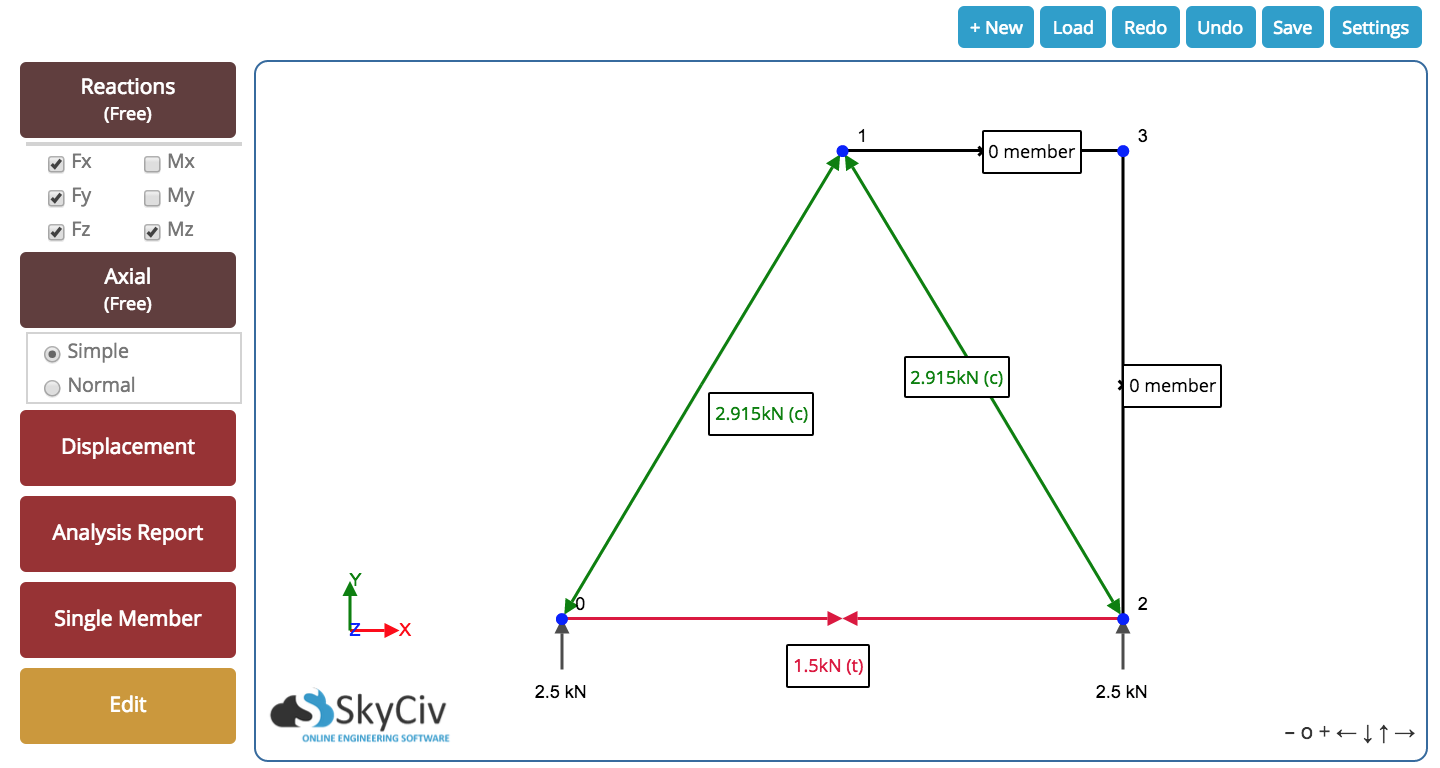
From the above equations, we solve for the reaction force at point B (the right support). In our example, this works out to be 2.5 kN in an upward direction. Now, if we take the sum of the forces in the y (vertical) direction, we find that support A (the left support) is also given as 2.5 kN.
Step 2: Consider one of the Supports:
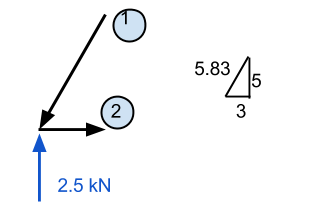
Now that we have the reaction forces we can start the analysis of the rest of this truss structure. Firstly, we look to one of our known forces – in this case, we will consider the left support reaction of +2.5 kN. Since we know this force occurs at this point, we will consider just this point in isolation. We repeat this process a number of times, so it is important to practice and learn the process in order to have a good grasp on how to solve axial forces in truss structures. So again, consider the first point at the support:
Zooming into this point, we see all the known forces acting on this point. From statics, we know that the forces in the x and y-direction both must sum to zero. Accordingly, if we know that there is an upward vertical force, then there must be a downward force to counteract it. Since we already have the value of an upward-facing force, then we will try to evaluate member number 1 first.
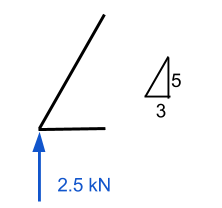
Here we require some knowledge of vectors. It is important to remember that all the forces must sum to zero for both the x and y-direction. In our example, the horizontal distance is 3m while the vertical is 5m – leaving us with the hypotenuse equal to approximately 5.83 m. Using this, we can deduce that the normal force component of member 1 is equal to (5.83)/(5) times the vertical force of 2.5 kN. This equates to 2.92 kN and MUST be a downward acting force if the point is to stay stationary.
Member 2 can be calculated in much the same way. If we know that member 1 is acting downwards, then we know it must also acting to the left. Accordingly, we know member 2 must be generating a force that is pulling the point to the right to maintain the forces in the x-direction. This value is calculated by (3/5.83) x 2.92 kN and is equal to 1.51 kN.
Step 3: Move to another point:
Having calculated the internal forces of the first member in our truss, we will now look to another point to repeat the process:
Again, we will zoom into the point of reference and consider all the known forces acting on the point:
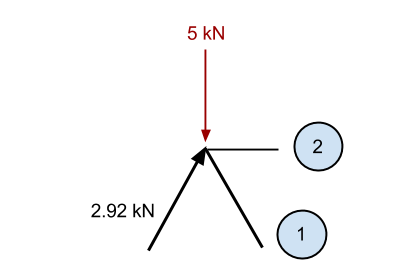
Much the same way as before, if we sum the known vertical component of the 2.92 kN member (2.5 kN in the vertical direction) and the – 5kN downward force, then we have excess in the downward direction of 2.5 kN (5 – 2.5). Accordingly, we know that member 1 must be causing a force in the upwards direction to keep the point static. This force must have a vertical component of 2.5 kN, and since it is at the same angle as the previous member, then the internal axial force must also be 2.92 kN.
Now we consider the forces in the x-direction. At this point, all the vertical force from member 1 is resisting the vertical force of the previously calculated member. This means the sum of forces in the x-direction is already zero. Accordingly, there can be no force in Member 2 or else the point will become unbalanced and no longer static.
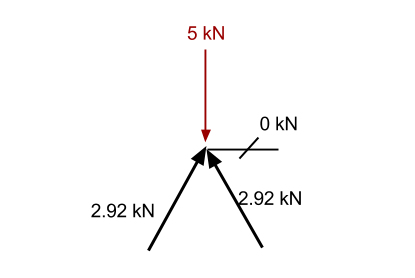
Step 4: Move to another point:
Looking at this point, we can see there is a special case. In this situation, any force pushing up will have no possible resisting action, as there is no other member that is able to provide a downward force to keep the point static. Accordingly, since the sum of forces must be zero, that member can have no force associated with it. It, therefore, has no force in it and is known as a Zero Member.
Again, if we look at summing the forces in the x-direction, we can see there is only one member that has any force in the x-direction. Accordingly, this must also have 0 axial force in order for the sum of forces to equal zero.

Final Solution
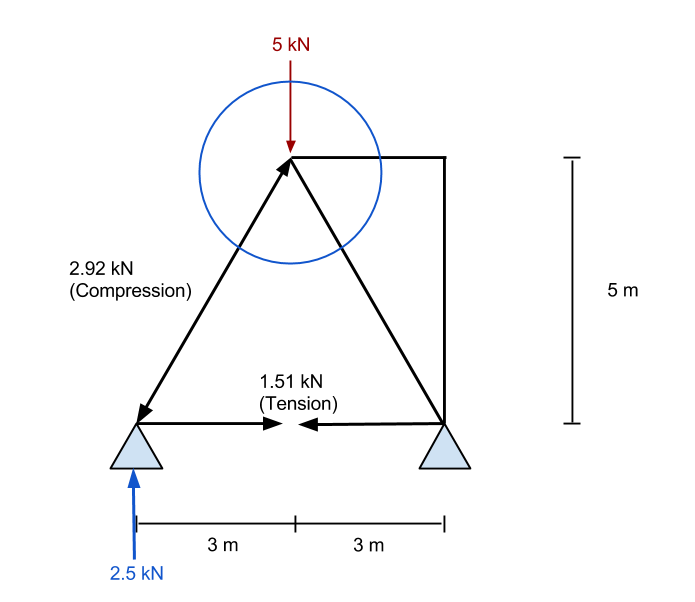
Finally, we end up with the following result for our truss. We can see all the resulting axial forces inside the member and the reactions at the supports. The following result was taken from our Free Truss Calculator – give it a go, it’s Free!
Simple Steps
- Always Start by calculating reactions at supports
- Pick a point with a known force and look at it in isolation
- Use vector geometry and the sum of forces = 0 to solve the other member forces
- Repeat the process until all members are solved
- Remember to look out for Zero Members
Relevant tutorial
- Solving truss by method of sections. Includes a video and step by step guide
SkyCiv Truss
SkyCiv Truss can calculate the method of joints automatically for you. Or try our Free Truss Calculator which will give you the final answer (no hand calculations).
To explore more functionality of SkyCiv software, sign up today to get started!


