The centroid or center of mass of beam sections is useful for beam analysis when the moment of inertia is required for calculations such as shear/bending stress and deflection. This article guides you through a simple process of how to calculate centroid and introduces you to SkyCiv Free Centroid Calculator.
How to Find Centroid
First of all, you need to know how to find centroid. Beam sections are usually made up of one or more shapes. So to find the centroid of an entire beam section area, it first needs to be split into appropriate segments. After this, the area and centroid of each individual segment need to be considered to find the centroid of the entire section.
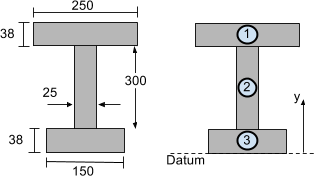
Consider the I-beam section shown below. To calculate the vertical centroid (in the y-direction) it can be split into 3 segments as illustrated:
Now we simply need to use the centroid equation for finding the vertical (y) centroid of a multi-segment shape:

We will take the datum or reference line from the bottom fo the beam section. Now let’s find Ai and yi for each segment of the I-beam section shown above so that the vertical or y centroid can be found.
[math]
\text{Segment 1:}\\
\begin{align}
{A}_{1} &= 250\times38 = 9500 {\text{ mm}}^{2}\\
{y}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \text{ mm}\\\\
\end{align}
[math]
[math]
\text{Segment 2:}\\
\begin{align}
{A}_{2} &= 300\times25 = 7500 {\text{ mm}}^{2}\\
{y}_{2} &= 38 + \tfrac{300}{2} = 188 \text{ mm}\\\\
\end{align}
[math]
[math]
\text{Segment 3:}\\
\begin{align}
{A}_{3} &= 38\times150 = 5700 {\text{ mm}}^{2}\\
{y}_{3} &= \tfrac{38}{2} =19 \text{ mm}\\\\
\end{align}
[math]

In the event that the cross-section is composed of two materials or a composite material, then one of the materials will have to be multiplied by the modular ratio such that the equation entire section becomes uniform.
[math]
n=\frac{E_{1}}{E_{2}}
[math]
Typically, E1 is the modulus of elasticity of the non-prevailing material, and E2 is the modulus of elasticity of the prevailing material, although whichever order that is preferred will not affect the solution of the centroid. Adjusting for the second material, the centroid equation becomes the following.
[math]
\bar{y}=\frac{\sum{A}_{i}{y}_{i}+\sum {n}{A}_{i}{y}_{i}}{\sum{A}_{i}+\sum {n}{A}_{i}}
[math]
Find centroid of beam with SkyCiv
Finding centroid of beam is important but calculating them by hands can be time-consuming. SkyCiv offers a Free Centroid Calculator that automates this process for you, helping you find the vertical (y) and horizontal (x) centroids of beam sections easily and accurately!
This tool is a free version of SkyCiv Section Builder, a comprehensive online section analysis software to analyze geometric, bending, shear and torsion section properties as well as FEA and reinforced concrete design. With this tool, you can create custom sections using predefined templates or define your own shapes with points, lines, or DXF imports from CAD.
To explore all the functionality SkyCiv Section Builder and experience the ease of modeling and analyzing your section, sign up for FREE today!
Related resources


