Moment of inertia is an important geometric property used in structural engineering. It is directly related to the amount of material strength your section has. Generally, a higher moment of inertia implies a greater strength in the section, resulting in reduced deflection when subjected to a load. The designation “moment of inertia” is a actually a widely used misnomer, as this property has nothing to do with inertia. The correct technical name is actually Second moment of area. This designation describes more accurately what is being measured this property, which can be though of roughly as a measure of how far out the section’s area is from the neutral axis.
Table of Contents
Moment of Inertia of a Rectangle Formula
The general formula used for determining the moment of inertia of a rectangle is:
[math] I_{xx}=\dfrac{BD^3}{12} , I_{yy}=\dfrac{B^3D}{12} [math]
Where the xx and yy refer to the particular axis, or direction, being considered.
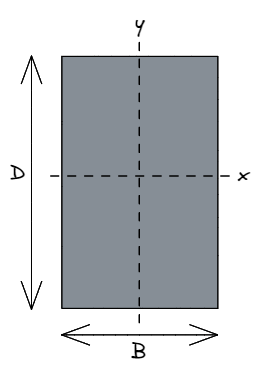
It is a common structural engineering convention that B refers to the width of the rectangle, parallel to a conventionally horizontal x-axis.
Similarly, D refers to the depth of the rectangle, parallel to a conventionally vertical y-axis.
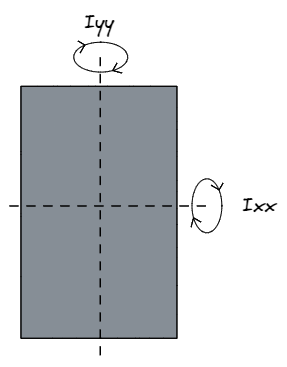
When structural engineers refer to Ixx they are referencing the strength of a section about the x-axis, meaning in a direction parallel to the D dimension, or y-axis. Similarly, Iyy refers to the strength about the y-axis, meaning in a direction parallel to the B dimension, or x-axis.
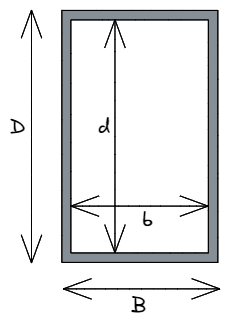
Rectangular Hollow Sections (RHS)
While engineers could hypothetically use solid rectangular sections when designing, this would use a significantly greater amount of raw material, with corresponding increases in weight and cost. It is much more common to use rectangular hollow sections (commonly referred to as an RHS). Here we can utilise the same equation defined above for the general rectangular case, however, we must subtract the inner hollow area of the rectangle:
[math] I_{xx}=\dfrac{BD^3}{12} – \dfrac{bd^3}{12} [math]
In this instance, lowercase b and d denote the size of the hollow area within the rectangle that we must subtract from the outer dimensions of the shape, being uppercase B and D. The difference between each corresponding dimension refers to the thickness of the material in that dimension – i.e. B – b = total thickness of the material parallel to the x-axis.
Besides the clear examples of weight and material use, why are hollow sections often described as more efficient than their solid counterparts?
Consider a beam undergoing a vertical load downwards. We expect the topmost fibres of the material to undergo a compressive force, while the corresponding bottom fibres will undergo a tensile force. The fibres along the neutral axis of the section (parallel to the section’s centroid) however, will experience neither compression nor tension, hence the name neutral axis.
Importantly, the magnitude of these compressive or tensile forces depend on the distance away from this neutral axis – material closer to the neutral axis needs to resist less force.
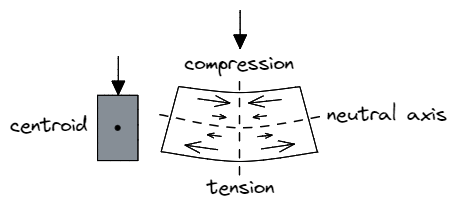
As a result, the inner material of a solid section resists only a small amount of force while occupying a large area, since the outermost material bears the most load! Removing this inner part of the section and making it hollow consequently improves the efficiency of the section in regard to its weight, cost, and material use.
Conclusion
In summary, the formula for determining the moment of inertia of a rectangle is Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. For rectangular hollow sections, the formula is Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.
The moment inertia is important for both bending moment force/stress and deflection. This is evident in their formulas, as in both cases, I (Moment of Inertia) is in the denominator:

Source: Bending Stress Formula
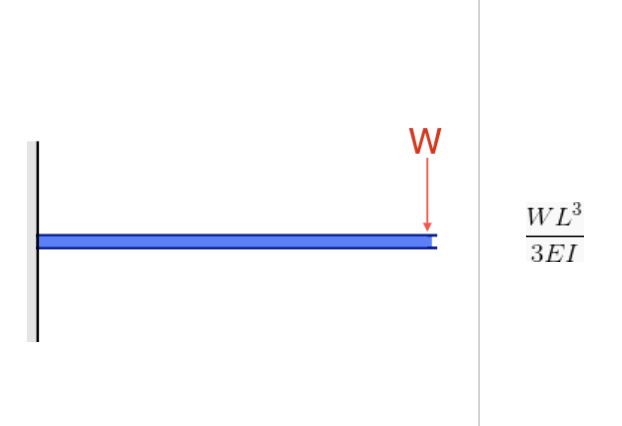
Source: Equation of Deflection in a Cantilever Beam
Moment of Inertia Calculator of a Circle
If you want to learn more, check out our tutorial on the Moment of Inertia of a Circle to see how circular and rectangular section shapes compare.
Free Moment of Inertia Calculator
Use our Free Moment of Inertia Calculator to experiment with the above calculations.
For a more detailed analysis, sign up to get started with our full SkyCiv Section Builder version!


