Composite sections involve more than one shape, made up of more than one material. SkyCiv’s Section Builder can perform calculations for composite shapes that involve stacking one shape on top / to the side of another such as with laminate beams. The method of calculation is the Transformed Section Method. The advantage of using our calculator is that most textbooks will only show you how to perform the transformation calculation on a simple rectangle. SkyCiv’s Section Builder is able to perform the transformation calculation on non-rectangular sections such as I-shapes, T-shapes, L-shapes and so on.

  Follow Us on YouTube Composite sections involving shapes within other shapes, such as steel rods within concrete blocks, are currently not supported. Send us an email if you wish to see this feature being implemented sooner.

Example: Concrete channel on top of steel I-Beam

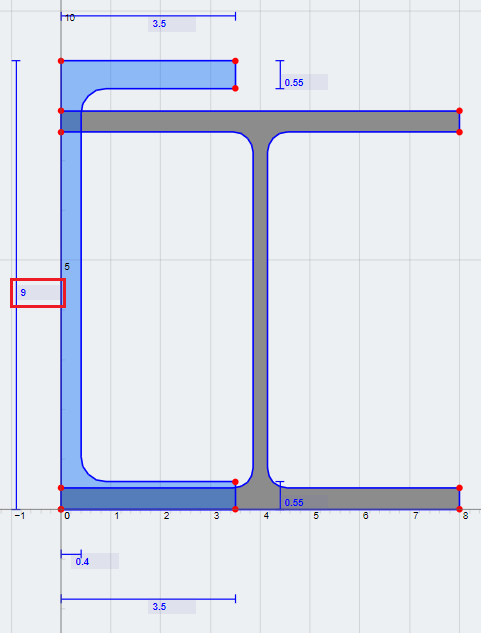
In this example, we’re going to create a composite section made up of a steel I-Beam and a concrete channel.

1) Make sure the ‘Clear Others’ checkbox is unticked while adding both sections.

2) Add the “I-Shape” and “Channel” onto the design area. Click into the channel’s height dimension and change it to be the same length as the I-beam’s width (i.e. 8 inches).

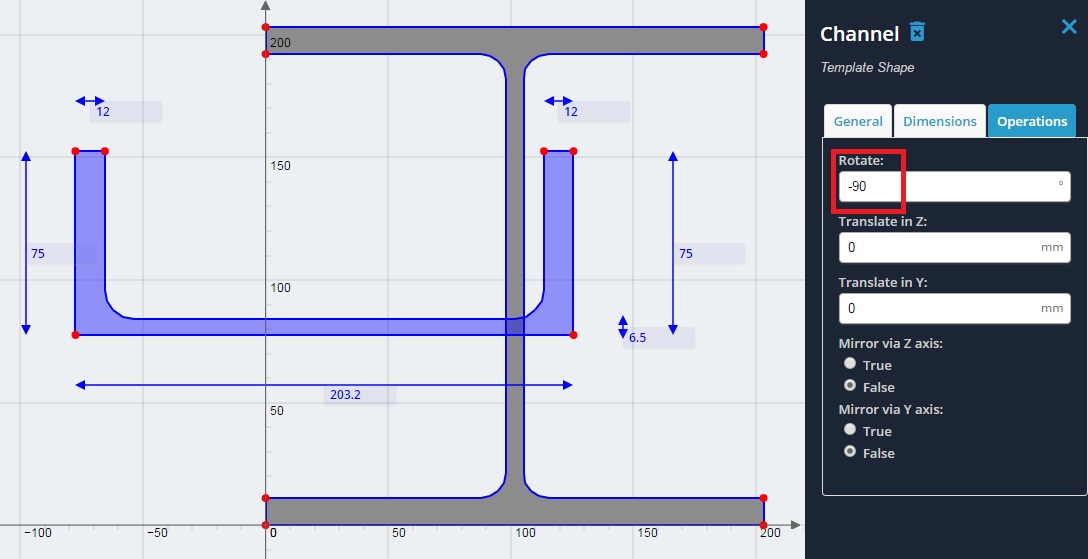
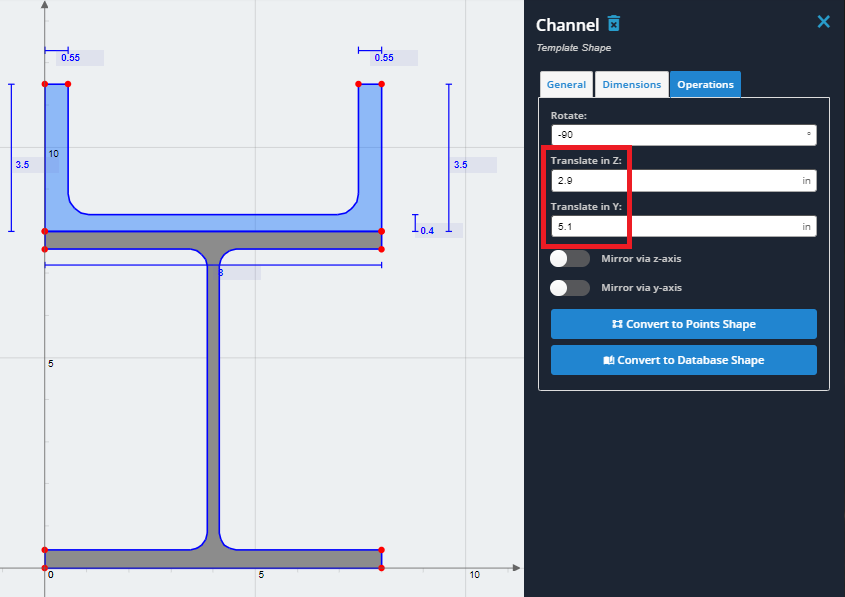
3) Rotate the channel by -90 degrees. Click into the ‘Operations’ tab and enter in -90 for the rotate value.

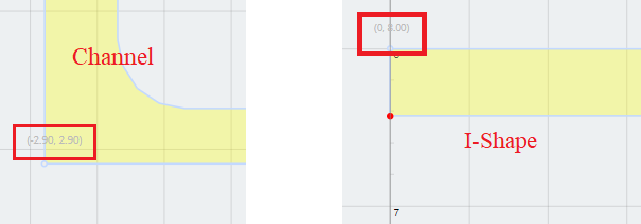
4) Stack the channel on top of the I-beam. Do this by hovering over the coordinates as shown, and performing some simple math. Note that the channel’s bottom left coordinates are (-2.90, -2.90), and the I-beam’s top left coordinates are (0, 8.0). To move the channel’s coordinate to the same place as the I-beam’s coordinate, simply do a final – initial calculation. I.e.

Z (horizontal) Translation distance = 0 – (-2.90) = 2.90

Y (vertical) Translation distance = 8.0 – 2.90 = 5.1

These are the values to translate the channel in the Z and Y axis directions respectively in the ‘Operations’ tab.

5) Select the I-beam and click the ‘General’ tab. This is where material properties can be changed. Note that by default, a shape will be assigned ‘Structural Steel’ as its material. Values are available to be changed for Young’s Modulus, Poisson’s Ratio, and Density. Leave these alone for this example. Note that if these properties are not visible, you may be using S3D’s integration of Section Builder. If so, then materials are edited in their own menu area.

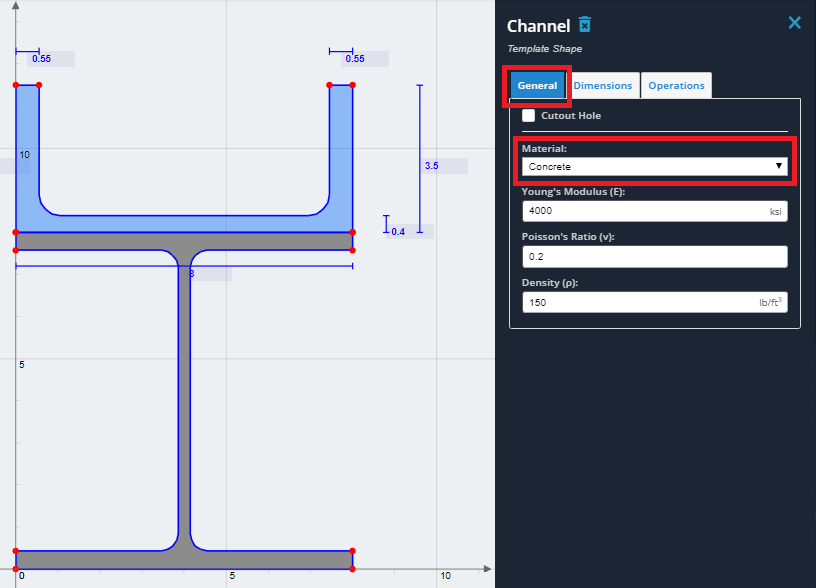
6) Select the channel and click the ‘General’ tab. In the ‘Material’ dropdown, select ‘Concrete’ from the list. Again, the material properties can be edited however for this example use the default concrete properties.

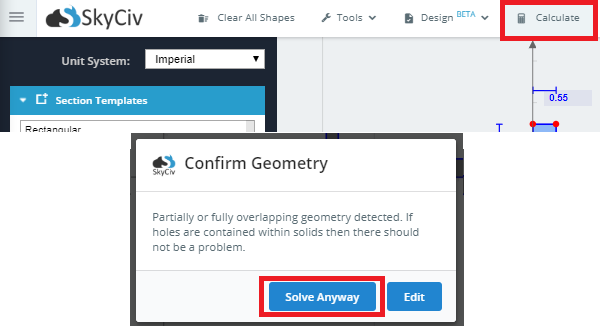
7) You’ve now successfully created a composite section. To calculate the section properties, click the ‘Calculate’ button on the top toolbar. If you see a pop up mentioning overlapping geometry, click ‘Solve Anyway’ as the geometries are just touching. Results will be presented for both the original section as well as the transformed section. An explanation of the results will be explored in the section on results.