Base Plate Design Example using AS 4100:2020 and AS 3600:2018
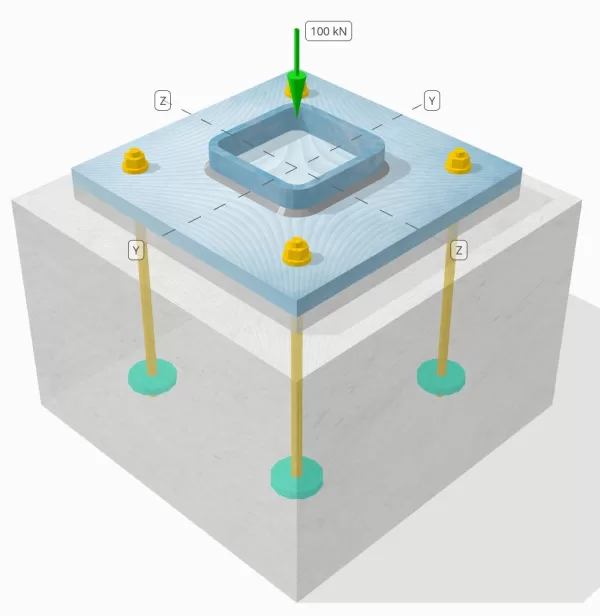
Problem Statement:
Determine whether the designed column-to-base plate connection is sufficient for a 100-kN compression load.
Given Data:
Column:
Column section: 50×10 SHS
Column area: 5260 mm2
Column material: AS/NZS 1163 Gr. C350
Base Plate:
Base plate dimensions: 350 mm x 350 mm
Base plate thickness: 20 mm
Base plate material: AS/NZS 3678 Gr. C250
Grout:
Grout thickness: 20 mm
Concrete:
Concrete dimensions: 450 mm x 450 mm
Concrete thickness: 300 mm
Concrete material: N28
Welds:
Weld size: 6 mm
Filler metal classification: E43XX
Compression load transferred through welds only? YES
Step-by-Step Calculations:
Check #1: Calculate concrete bearing capacity
To start, we determine the bearing areas per AS 3600:2018 Clause 12.6:
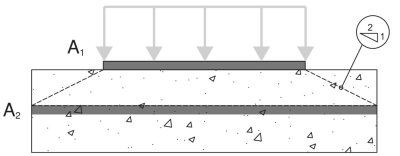
A1 – Base plate bearing area
A2 – Concrete support bearing area, projected at a 2:1 slope
\(
A_1 = L_{bp} B_{bp} = 350 \, \text{mm} \times 350 \, \text{mm} = 122500 \, \text{mm}^2
\)
\(
A_2 = N_{A2} B_{A2} = 450 \, \text{mm} \times 450 \, \text{mm} = 202500 \, \text{mm}^2
\)
From there, we calculate the concrete bearing capacity, expressed as an equivalent force. We use ASI Design Guide 07 1st Ed. Section 9.1 as reference.
\(
\phi N_c = \min \left( \phi 0.9 \left( f’_c \right) A_1 \sqrt{\frac{A_2}{A_1}}, \phi 1.8 \left( f’_c \right) A_1 \right)
\)
\(
\phi N_c = \min \left( 0.6 \times 0.9 \times \left( 28 \, \text{MPa} \right) \times 122500 \, \text{mm}^2 \times \sqrt{\frac{202500 \, \text{mm}^2}{122500 \, \text{mm}^2}}, 0.6 \times 1.8 \times \left( 28 \, \text{MPa} \right) \times 122500 \, \text{mm}^2 \right)
\)
\(
\phi N_c = 2381.4 \, \text{kN}
\)
Since 100 kN <2381.4 kN, the concrete bearing capacity is sufficient.
Check #2: Calculate weld capacity
To evaluate the weld capacity, we first determine the total weld length based on the column dimensions:
\(
L_{\text{weld}} = 2 \left( b_{\text{col}} – 2 r_{\text{col}} – 2 t_{\text{col}} \right) + 2 \left( d_{\text{col}} – 2 r_{\text{col}} – 2 t_{\text{col}} \right)
\)
\(
L_{\text{weld}} = 2 \times \left( 150 \, \text{mm} – 2 \times 15 \, \text{mm} – 2 \times 10 \, \text{mm} \right) + 2 \times \left( 150 \, \text{mm} – 2 \times 15 \, \text{mm} – 2 \times 10 \, \text{mm} \right) = 400 \, \text{mm}
\)
With this, we can calculate the stress per unit length of weld, assuming the 100 kN load is evenly distributed:
\(
v^*_w = \frac{N_x}{L_{\text{weld}}} = \frac{100 \, \text{kN}}{400 \, \text{mm}} = 0.25 \, \text{kN/mm}
\)
After that, we determine the weld capacity per unit length using AS 4100:2020 Clause 9.6.3.10:
\(
\phi v_w = \phi 0.6 f_{uw} E_w k_r = 0.8 \times 0.6 \times 430 \, \text{MPa} \times 4.243 \, \text{mm} \times 1 = 0.87576 \, \text{kN/mm}
\)
Since 0.87576 kN/mm < 0.25 kN/mm, the weld capacity is sufficient.
Check #3: Calculate base plate flexural yielding capacity due to compression load
The flexural capacity of the base plate depends on its dimensions. If the plate is too wide, it will require thicker material. Selecting the right base plate size for a given load requires experience, and performing multiple calculations can be time-consuming. The SkyCiv Base Plate Design software simplifies this process, enabling fast and efficient modeling and analysis in just seconds.
We use ASI Design Guide 07, 1st Ed., Table 7 to check the base plate flexural yielding capacity. First, we determine the kx factor.
\(
k_x = 1.65 \left( \frac{\sqrt{L_{bp} B_{bp}}}{b_{\text{col}}} \right) = 1.65 \times \left( \frac{\sqrt{350 \, \text{mm} \times 350 \, \text{mm}}}{150 \, \text{mm}} \right) = 3.85
\)
Next, we calculate the concrete bearing strength in terms of stress over area. Refer to Check #1 for the calculated bearing capacity.
\(
\phi f_b = \frac{\phi N_c}{L_{bp} B_{bp}} = \frac{2381.4 \, \text{kN}}{350 \, \text{mm} \times 350 \, \text{mm}} = 19.44 \, \text{MPa}
\)
We then use this value to obtain the X factor.
\(
X = \frac{4 N_c^*}{\phi f_b (2 b_{\text{col}})^2} = \frac{4 \times 100 \, \text{kN}}{19.44 \, \text{MPa} \times (2 \times 150 \, \text{mm})^2} = 0.22862
\)
Now, let us use the calculated kx and X factors to evaluate the λ (lambda) factor.
\(
\lambda = \min \left( \frac{k_x \sqrt{X}}{1 + \sqrt{1 – X}}, 1.0 \right) = \min \left( \frac{3.85 \times \sqrt{0.22862}}{1 + \sqrt{1 – 0.22862}}, 1 \right) = 0.98008
\)
We then calculate the cantilever length of the base plate experiencing the bearing load. According to ASI Design Guide 07, 1st Ed., Sections 6.1 and 9.1–9.2, the cantilever length is as shown:
\(
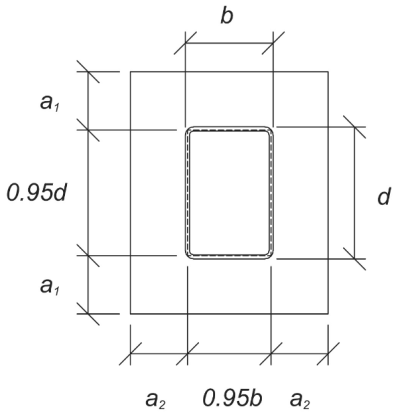
l = \max \left( \frac{L_{bp} – 0.95 d_{\text{col}}}{2}, \frac{B_{bp} – 0.95 b_{\text{col}}}{2}, \lambda 0.306 \sqrt{d_{\text{col}} b_{\text{col}}} \right)
\)
\(
l = \max \left( \frac{350 \, \text{mm} – 0.95 \times 150 \, \text{mm}}{2}, \frac{350 \, \text{mm} – 0.95 \times 150 \, \text{mm}}{2}, 0.98008 \times 0.306 \times \sqrt{150 \, \text{mm} \times 150 \, \text{mm}} \right)
\)
\(
l = 103.75 \, \text{mm}
\)
Considering this critical section of the base plate, let’s calculate the flexural yield stress. This is a rearranged equation from ASI Design Guide 07, 1st Ed., Section 9.2, with reference to Section 6.1.
\(
f^* = \frac{2 N_x l^2}{B_{bp} L_{bp} (t_{bp})^2}
\)
\(
f^* = \frac{2 \times 100 \, \text{kN} \times 103.75 \, \text{mm}^2}{350 \, \text{mm} \times 350 \, \text{mm} \times (20 \, \text{mm})^2} = 43.935 \, \text{MPa}
\)
The final step is to calculate the yielding capacity of the base plate using AS 4100:2020, Clause 5.2.1.
\(
\phi f_y = \phi f_{y_{bp}} = 0.9 \times 250 \, \text{MPa} = 225 \, \text{MPa}
\)
Since 43.935 MPa < 225 MPa, the base plate flexural capacity is sufficient.
Design Summary
The SkyCiv Base Plate Design software can automatically generate a step-by-step calculation report for this design example. It also provides a summary of the checks performed and their resulting ratios, making the information easy to understand at a glance. Below is a sample summary table, which is included in the report.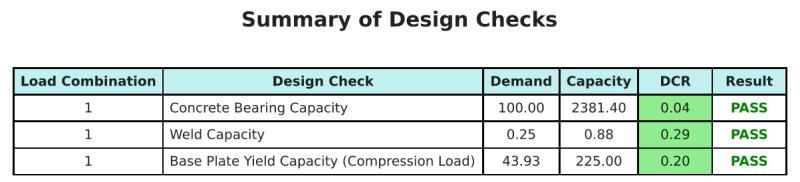
SkyCiv Sample Report
Click here to download a sample report.
Purchase Base Plate Software
Purchase the full version of the base plate design module on its own without any other SkyCiv modules. This gives you a full set of results for Base Plate Design, including detailed reports and more functionality.
