Base Plate Design Example using AISC 360-22 and ACI 318-19
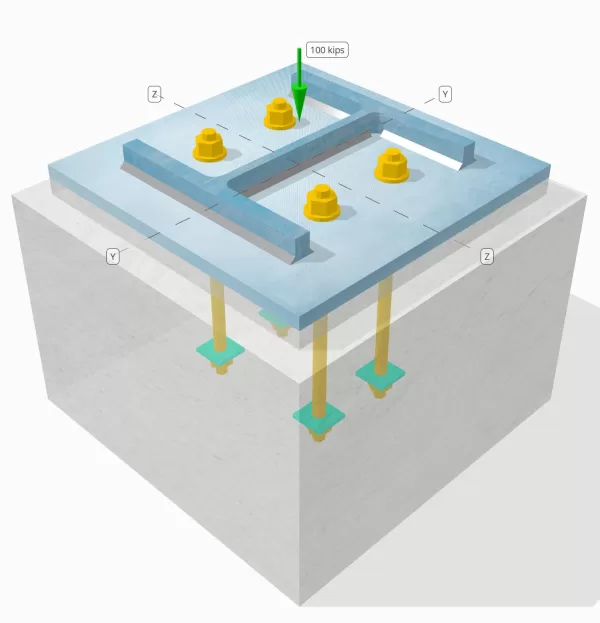
Problem Statement:
Determine whether the designed column-to-base plate connection is sufficient for a 100-kip compression load.
Given Data:
Column:
Column section: W12x96
Column area: 28.200 in2
Column material: A992
Base Plate:
Base plate dimensions: 18 in x 18 in
Base plate thickness: 3/4 in
Base plate material: A36
Concrete:
Concrete dimensions: 21 in x 21 in
Concrete thickness: 14 in
Concrete material: 3000 psi
Welds:
Weld size: 5/16 in
Filler metal classification: E70XX
Compression load transferred through welds only? YES
Step-by-Step Calculations:
Check #1: Calculate bearing capacity of column
Column loads are typically transferred to the base plate through direct bearing.
We begin by calculating the bearing capacity of the column using AISC 360-22 Eq. J7-1:
\(\phi R_n = \phi 1.8 F_{y\_col} A_{col} = 0.75 \times 1.8 \times 50 \text{ ksi} \times 28.2 \text{ in}^2 = 1903.5 \text{ kip}\)
Since 100 kips < 1903.5 kips, the column bearing capacity is sufficient.
Additionally, because the full compression load is transferred through the welds, full-contact bearing surfaces as per AISC 360-22 Chapter M4.4 are not required. We need to make sure that the weld has enough capacity to transfer the load.
Check #2: Calculate weld capacity
To evaluate the weld capacity, we first determine the total weld length based on the column dimensions:
\( L_{weld} = 2b_f + 2 \left( d_{col} – 2t_f – 2r_{col} \right) + 2 \left( b_f – t_w – 2r_{col} \right) \)
\( L_{weld} = 2 \times 12.2 \text{ in} + 2 \times \left( 12.7 \text{ in} – 2 \times 0.9 \text{ in} – 2 \times 0.6 \text{ in} \right) + 2 \times \left( 12.2 \text{ in} – 0.55 \text{ in} – 2 \times 0.6 \text{ in} \right) = 64.7 \text{ in} \)
With this, we can now calculate the stress per inch of weld, assuming the 100-kip load is evenly distributed:
\( r_u = \frac{N_x}{L_{weld}} = \frac{100 \text{ kip}}{64.7 \text{ in}} = 1.5456 \text{ kip/in} \)
After that, we determine the weld capacity per length using AISC 360-22 Eq. J2-4:
\( \phi r_{n} = \phi 0.6 F_{exx} E_{w} k_{ds} = 0.75 \times 0.6 \times 70 \text{ kso} \times 0.221 \text{ in} \ times 1 = 6.9615 \text{ kip/in}\)
Since 1.54 kpi < 6.96 kpi, the weld capacity is sufficient.
Check #3: Calculate base plate flexural yielding capacity due to compression load
The flexural capacity of the base plate depends on its dimensions. If the plate is too wide, it will require thicker material. Selecting the right base plate size for a given load requires experience, and performing multiple calculations can be time-consuming. The SkyCiv Base Plate Design software simplifies this process, enabling fast and efficient modeling and analysis in just seconds.
First, we determine the critical cantilever length, which is the larger of dimension m and dimension n. It should also not be less than \( \frac{ \sqrt{d_{col}b_{f}}}{4} \).
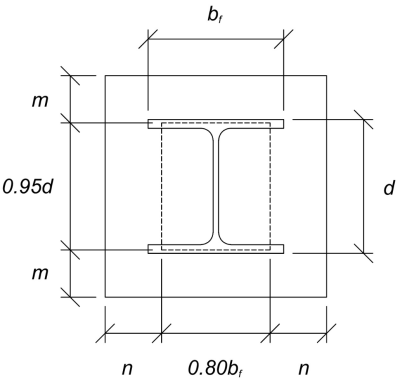
\( l = max \left( \frac{L_{bp} – 0.95 d_{col}}{2}, \frac{B_{bp} – 0.8 b_{f}}{2},\frac{ \sqrt{d_{col}b_{f}}}{4} \right) \)
\( l = max \left( \frac{18 \text{ in} – 0.95 \times 12.7\text{ in}}{2}, \frac{18 \text{ in} – 0.8 \times 12.2 \text{ in}}{2},\frac{ \sqrt{18 \text{ in} \times 12.2 \text{ in}}}{4} \right)\)
\(l = 4.12 \text{ in}\)
Once the critical length is identified, we calculate the applied moment per unit length, assuming the full compression load is uniformly distributed over the base plate area:
\( m_{u} = \left( \frac{N_{x}}{B_{bp} L_{bp}}\right) \left( \frac{l^{2}}{2}\right)\)
\( m_{u} = \left( \frac{100 \text{ kip}}{18 \text{ in} \times 18 \text{ in}}\right) \times \left( \frac{4.12 \text{ in}^2}{2}\right)\)
Now, using AISC 360-22 Eq. F2-1, we compute the flexural capacity per unit length:
\(\phi m_{n} = \phi F_{y\_bp}\left(\frac{t_{bp}^{2}}{4}\right) = 0.9 \times 36 \text{ ksi} \times \left(\frac{\left(0.75 \text{ in}\right)^2}{4}\right) = 4.5562 \text{ kip-in/in}\)
Since 2.62 kip-in/in < 4.55 kip-in/in, the base plate flexural capacity is sufficient.
Check #4: Concrete bearing capacity
The final check ensures that the concrete can support the applied load. While a wider concrete base increases bearing capacity, an efficient design must balance strength and cost-effectiveness. Now, let’s determine if our concrete support has sufficient capacity.
To start, we determine the bearing areas:
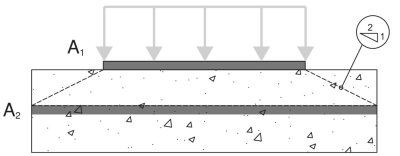
A1 – Base plate bearing area
A2 – Concrete support bearing area, projected at a 2:1 slope
\(A_1 = L_{bp} B_{bp} = 18 \, \text{in} \times 18 \, \text{in} = 324 \, \text{in}^2\)
\(A_2 = N_{A_2} B_{A_2} = 21 \, \text{in} \times 21 \, \text{in} = 441 \, \text{in}^2\)
From there, we apply AISC 360-22 Eq. J8-2 to calculate the concrete bearing capacity:
\(\phi P_p = \phi \left( \min \left( 0.85 \, f’_c \, A_1 \sqrt{\frac{A_2}{A_1}}, \, 1.7 \, f’_c \, A_1 \right) \right)\)
\(\phi P_p = 0.65 \times \left( \min \left( 0.85 \times (3 \, \text{ksi}) \times 324 \, \text{in}^2 \times \sqrt{\frac{441 \, \text{in}^2}{324 \, \text{in}^2}}, \, 1.7 \times (3 \, \text{ksi}) \times 324 \, \text{in}^2 \right) \right)\)
\(\phi P_p = 626.54 \, \text{kip}\)
Since 100 kips < 626.54 kips, the concrete bearing capacity is sufficient.
Design Summary
The SkyCiv Base Plate Design software can automatically generate a step-by-step calculation report for this design example. It also provides a summary of the checks performed and their resulting ratios, making the information easy to understand at a glance. Below is a sample summary table, which is included in the report.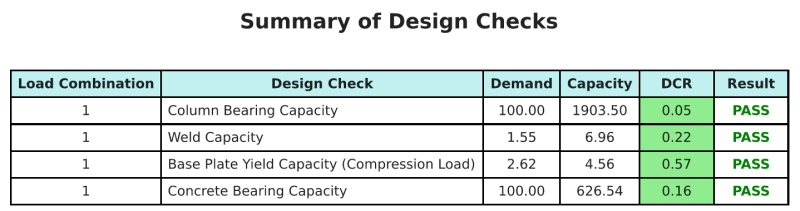
SkyCiv Sample Report
Click here to download a sample report.
Purchase Base Plate Software
Purchase the full version of the base plate design module on its own without any other SkyCiv modules. This gives you a full set of results for Base Plate Design, including detailed reports and more functionality.
