目次
概要概要 – 慣性モーメントとは?
構造工学の文脈で, 慣性モーメントは、構造要素が曲げ力やねじり力に抵抗する能力を決定するために使用される断面特性です。. 通常、これは負荷がかかった状態でのセクションの剛性と強度を示す非常に優れた指標です。. 慣性モーメントが高いということは、構造が曲げやたわみに対する耐性を備えていることを意味します。, 梁の設計において重要な要素となる, コラム, およびその他の耐荷重コンポーネント. 補足として: 場合によっては、これは誤って次の瞬間として定義されます。 詳細な内訳, しかし、これは正しくありません. 慣性モーメントの別名は次のとおりです。: 面積慣性モーメント, または次の瞬間 変換されたセクションの結果とともに結果.
例 – 梁断面の慣性モーメントの計算方法
ビームセクションの慣性モーメントを見つける前に (梁断面の断面二次モーメントとも呼ばれます), その重心 (または重心) 知らなければならない. 例えば, その水平の周りの断面の慣性モーメント (XX) 軸が必要で、次に垂直 (そして) 最初に重心が必要になります (チュートリアルをご覧ください ビーム断面の重心を計算する そして 静的/断面一次モーメントの計算).
始める前に, 私たちを探していたなら 慣性モーメントの計算機 詳細はリンクをクリックしてください. これは重心を計算します, 慣性モーメント, およびその他の結果、さらには段階的な計算を示します! しかし、今のところ, ステップバイステップガイドと慣性モーメントの計算方法の例を見てみましょう:
ステップ 1: ビームセクションをパーツに分割する
断面二次モーメントを計算するとき, 小さなセグメントの慣性モーメントを計算する必要があります. それらを単純な長方形のセクションに分割してみてください. 例えば, 以下のIビームのセクションを検討してください, 重心チュートリアルでも紹介されました. このセクションを分割することにしました 3 長方形セグメント:
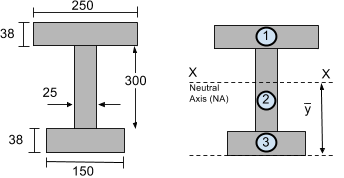
ステップ 2: 中立軸を計算する (NA)
中立軸 (NA) または、水平XX軸は重心または重心にあります. セントロイドのチュートリアルでは, このセクションの重心は以前に 216.29 セクションの下部からmm – これは私たちの 形状の重心を見つける方法 チュートリアル. これらは、私たちから簡単に計算することもできます。 この記事では、図心を計算する簡単なプロセスについて説明します。 または共通から 重心方程式.
重心の計算, または中立軸, に不可欠です ビームの慣性モーメントを計算する方法, 慣性モーメントが作用する軸なので.
ステップ 3: 慣性モーメントを計算する
セクションの総慣性モーメントを計算するには、 “平行軸定理”:

3つの長方形のパーツに分割したので, これらの各セクションの慣性モーメントを計算する必要があります. 重心軸を中心とした長方形の慣性モーメント方程式は、:
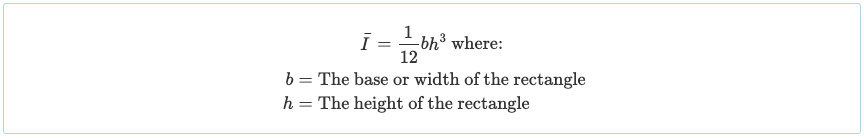
他の形状の慣性モーメントは、教科書の表/裏、またはこのガイドからしばしば述べられています。 慣性モーメント形状. ただし、ビーム断面では長方形の形状が非常に一般的です, おそらく覚える価値がある.
これで、使用する必要があるすべての情報が揃いました。 “平行軸定理” Iビーム断面の総慣性モーメントを求めます. 慣性モーメントの例:

ビーム断面のモーメント領域の計算に関するガイドがあります. この結果は構造工学では重要であり、ビームのたわみの重要な要素です. チュートリアルを楽しんでいただき、コメントをお待ちしております. 詳細については, のチュートリアルにアクセスしてください 慣性モーメントの式と方程式.
公式と方程式
各セクションタイプ (長方形の, アイビーム, 円形) 迅速な計算のための独自の計算式があります. これらは、エンジニアがこの重要な特性を迅速かつ簡単に計算できるようにする簡略化された方程式です。.
方程式は上記の手順を簡略化したものです. 例えば, 中空長方形の慣性モーメントの公式は、基本的には大きなセクションの MOI です。 – 小さいほうの (内部) セクション:

[数学] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [数学]
SkyCiv は、共通の便利なリソースをまとめました。 慣性モーメントの計算式.
電卓
慣性モーメントの求め方にはいろいろな方法があります, そのうちの 1 つは、ソフトウェアを使用してプロセスを簡単にすることです。.
SkyCivセクションビルダー 慣性モーメント計算機をはるかに超えた、完全に機能する断面設計ツールです。. また、慣性モーメントを見つける方法の段階的な計算も示します。:
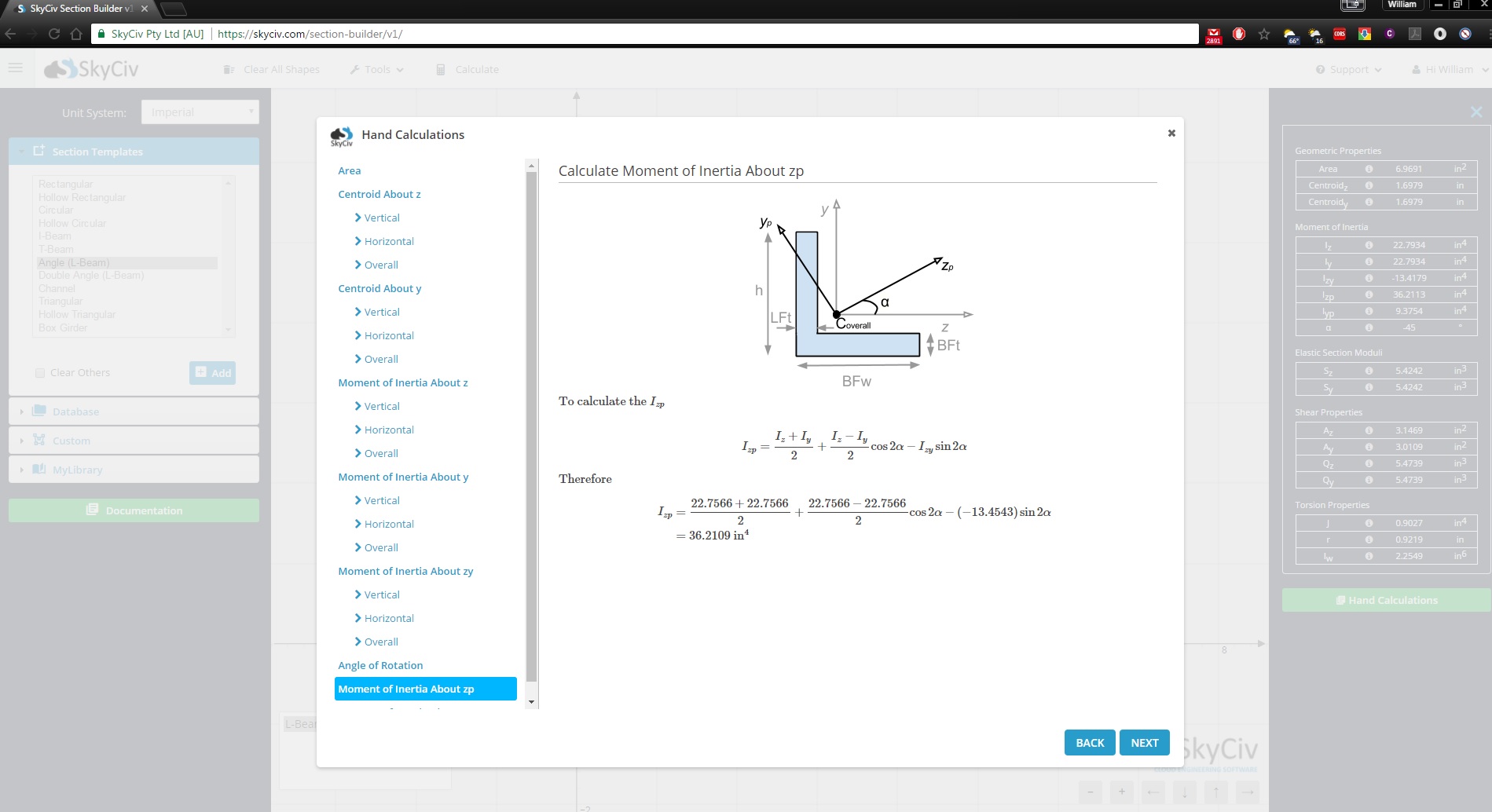

今すぐサインアップして SkyCiv ソフトウェアについて詳しく調べてください, または予約する 無料デモ 既存ユーザー向けのエンジニアリング プロジェクトを支援するため!
さらに, SkyCivには無料があります 断面特性計算ツール クイック デザイン ライブラリの一部として. 簡易的なツールです, ただし、一般的な断面形状の慣性モーメントも計算されます。.
練習問題
質問 1: 長方形セクション
問題: 慣性モーメントを計算する (Ixx と Iyy) 幅のある長方形のセクションの場合 (b) の 200 mmと高さ (h) の 300 んん.
解決: 長方形の慣性モーメントの公式は次のとおりです。:
与えられた値を代入する:
- b=200 mm
- h=300 mm
Ixxの場合:
いいのために:
質問 2: アイビーム
問題: 長軸の慣性モーメントを計算する (Ixx) 以下の寸法の I ビーム断面の:
- 上フランジ幅 (TFw) = 6 に
- 上フランジの厚さ (TFt) = 0.43 に
- セクションの深さ = 6 に
- ウェブの厚さ (Wt) = 0.29 に
- 下フランジ幅 (BFw) = 6 に
- 底フランジの厚さ (BFt) = 0.43 に

解決:


