ACIに準拠した単杭設計 318 (2014)

杭は長くて細い部材で、上部構造からより深い土や適切な支持力のある岩に荷重を伝達します。. 杭に使用される材料には、木材が含まれる場合があります, 鋼, とコンクリート. 地面への杭の設置は推進されるかもしれません, ドリル, またはジャッキで杭頭に接続します. 多くの要因, サイトの状態など, 土壌タイプ, 荷重の伝達, 杭の種類と設置を分類するために考慮されます. この記事では、米国コンクリート学会に準拠したコンクリート杭の設計に焦点を当てます。 (ACI) 318 – 2014.

SkyCiv Foundation Designモジュールには、American ConcreteInstituteに準拠した杭の設計が含まれています (ACI 318) およびオーストラリアの基準 (なので 2159 & 3600).

SkyCivのFoundationDesignソフトウェアを試してみたい? 私たちの無料ツールを使用すると、ユーザーはダウンロードやインストールなしで耐荷重計算を実行できます!

基礎設計計算機

杭の耐荷力

一般的に, 杭にかかる垂直荷重は、杭の端部支持によって支えられます。, そしてその長さに沿って発達した皮膚摩擦抵抗. 究極の負荷容量 (Q_U) 式で表されるものとする (1). 安全率は、許容負荷容量を計算するために適用されます (Q_あ).

\({Q}_{あなた} = {Q}_{p} + {Q}_{s}\) (1)

Q_U =究極の負荷容量

Q_P =エンドベアリング抵抗

Q_S =皮膚摩擦抵抗

\({Q}_{あ} = frac{{Q}_{U}}{FOS} \) (2)

Q_あ =許容負荷容量

FOS =安全率

より詳細なガイドについて, 計算に関する記事をご覧ください 皮膚摩擦抵抗とエンドベアリング能力.

単杭の構造強度

杭も軸力を受けます, 剪断力, と曲げモーメント, そのため、柱と同様に構造的に設計されています. セクション 10.5.1.1 すべての因数分解された荷重は、対応する設計強度を超えてはならないことを述べています.

\( {øP}_{N} ≤ {P}_{U} \) (3a)

\( {痛い}_{N} ≤ {M}_{U} \) (3b)

\( {øV}_{N} ≤ {V }_{U} \) (3c)

P_U, M_U, V _U =ファクタリングされた軸, 曲げモーメント, せん断荷重

P_N, M_N, V _N =公称軸方向, 曲げモーメント, せん断荷重

ø=強度低下係数 (テーブル 1)

強度低下係数(ϕ)
アキシャル	0.65-0.90
曲げ	0.65-0.90
剪断	0.75

テーブル 1: 強度低下係数 (テーブル 21.2.1, ACI 318-14)

単一杭のせん断耐力 (øV_N)

公称せん断強度は、コンクリートと鉄筋のせん断耐力の寄与を組み合わせたものと同等でなければなりません。.

コンクリートのせん断強度 (V _c)

せん断耐力へのコンクリートの寄与は、式に示すように計算されます (4) セクションで定義されています 22.5.5.1 ACIの 318-14.

\( {V }_{c} = 0.17 ×λ× sqrt{fc ’} ×b×d \) (4)

λ=具体的な修正係数= 1 (普通重量コンクリート, テーブル 19.2.4.2)

fc’ =コンクリートの強度

b =杭の幅または直径

d = 0.80 ×杭の深さ (セクション 22.5.2.2)

棒鋼のせん断強度 (V _s)

せん断耐力に対する横方向のせん断補強材の寄与は、方程式間の最小値として計算されます (5) そして (6).

\( {V }_{s} = 0.066 [object Window]{fc ’} ×b×d \) (5)

\( {V }_{s} = frac{{あ}_{v} × {f}_{yt} ×d }{s} \) (6)

あ_V =せん断鉄筋の面積

f_yt =せん断鉄筋の降伏強度

s =せん断鉄筋の中心間の間隔

公称せん断強度 (øV_N)

方程式の出力を要約する 4-6 杭の公称せん断強度になります. 強度低下係数 (ø) に等しいものとする 0.75 表で定義されているように 22.2.1 ACIの 318-14.

\( {øV}_{N} =ø× ({V }_{c} + {V }_{s}) ≤ {øV}_{U} \) (7)

基礎設計計算機

単一杭の軸方向および曲げ能力 (øP_N, 痛い_N )

軸方向および曲げ能力は、相互作用図を使用してチェックされます. この図は、純粋な曲げ点から平衡点に達するまでの荷重の増加によって引き起こされる曲げおよび軸方向の容量の動作を視覚的に表したものです。.

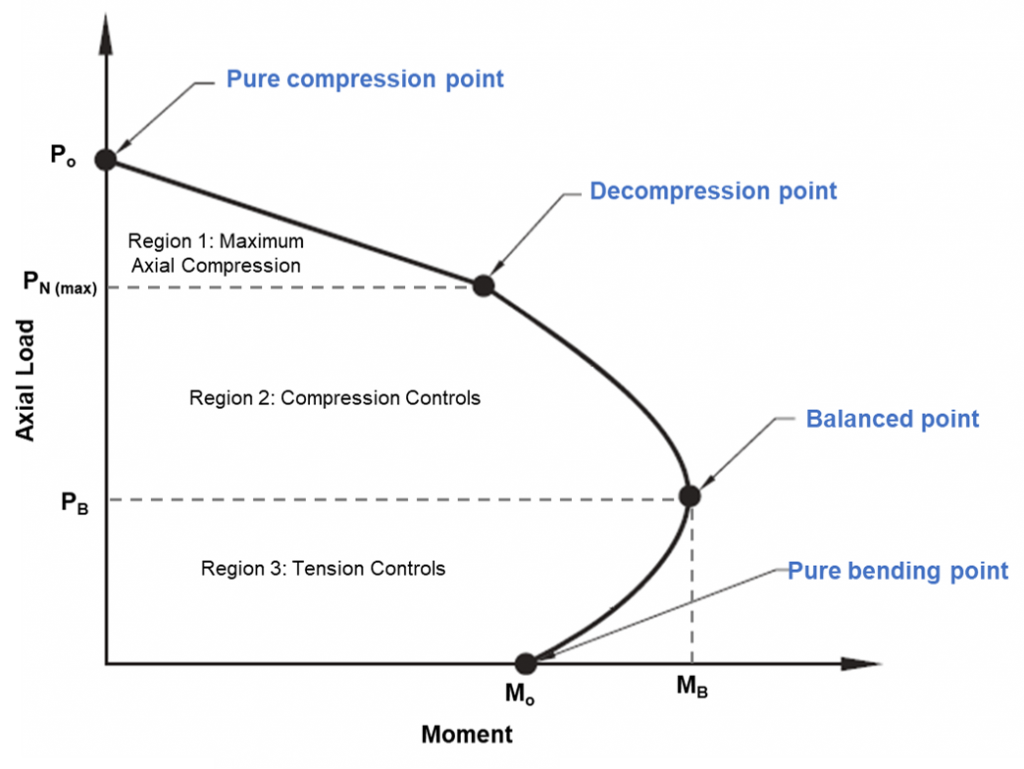
図 1: カラム相互作用図

列の相互作用図

図の純粋な圧縮ポイントは、パイルが純粋に圧縮に失敗する場所です。. この時点で, 軸方向の荷重がセクションのプラスチック重心に適用され、曲げることなく圧縮されたままになります. 線形補間により減圧点までの純粋な圧縮点間の杭の強度を計算できます. 減圧点は、極限圧縮繊維でのコンクリートひずみがに等しい場所です。 0.003, 極限引張繊維のひずみはゼロです. 純粋な曲げ点は、軸方向の耐荷重がゼロになる場所です。. 減圧点から純粋な曲げ点への移行の間, バランスの取れた状態が達成されます. この時点で, コンクリートのひずみは限界にあります (e_c= 0.003), 外側の鋼のひずみが降伏に達する (e_s= 0.0025). 図の外側の軸方向荷重と曲げモーメントの任意の組み合わせは、故障の原因になります.

設計の最大公称軸方向圧縮強度 (øP_N)

セクションの設計軸方向強度は、以下に限定されるものとします。 80-85% 偶発的な偏心を説明するための公称軸方向強度の.

\( {øP}_{N} =ø× {P}_{の} \) (8a)

\( {P}_{の} = F× [0.85 × {f}_{c} × ({あ}_{g} – {あ}_{st}) + ({f}_{そして} × {あ}_{st}) ] \) (8b)

F = 0.80 (ネクタイ)

F = 0.85 (螺旋)

あ_G =杭断面の総面積

あ_st =縦棒鋼の総面積

f_そして =棒鋼の降伏強度

公称曲げ強度 (痛い_N)

列の相互作用図の作成には、Pの一連の値のプロットが含まれます。_N そしてM_N. Pの値_N 引張力と圧縮力の合計に相当するものとする, 図2aおよび2bに示すように, 対応するM_N 中立軸の周りでこれらの力を解決することによって計算されます. これらの力には、圧縮領域に作用する圧縮力と、圧縮または引張のいずれかである可能性がある各鉄筋によって加えられる力が含まれます。. 提示された方程式を使用して相互作用図を作成するための一般的な手順を以下に示します。.

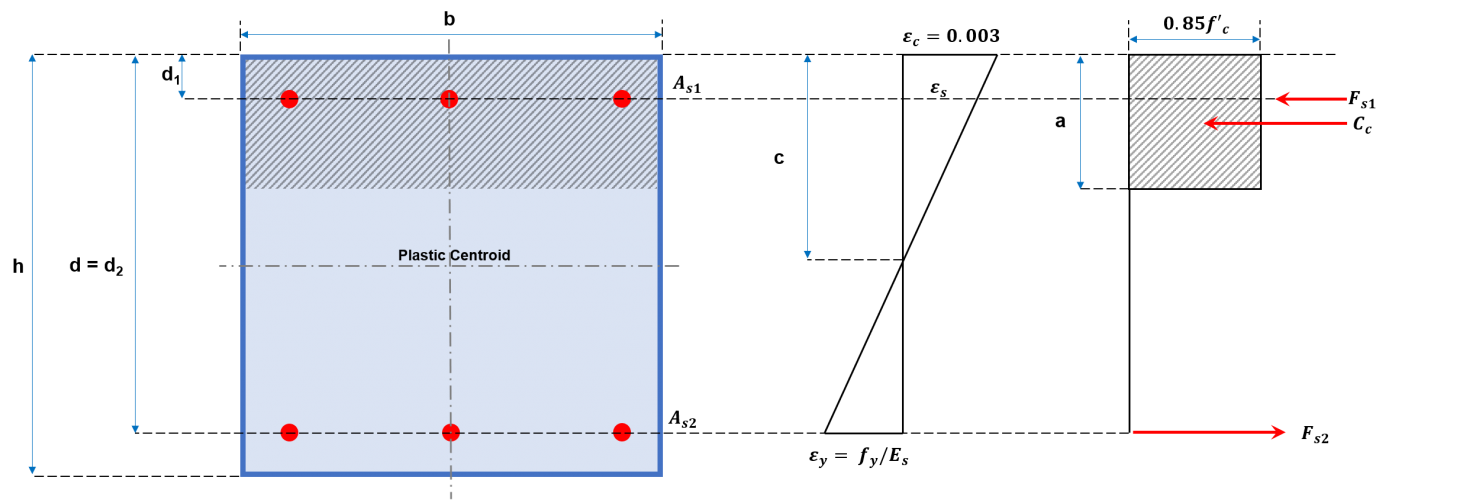
図2a: 長方形の柱の断面

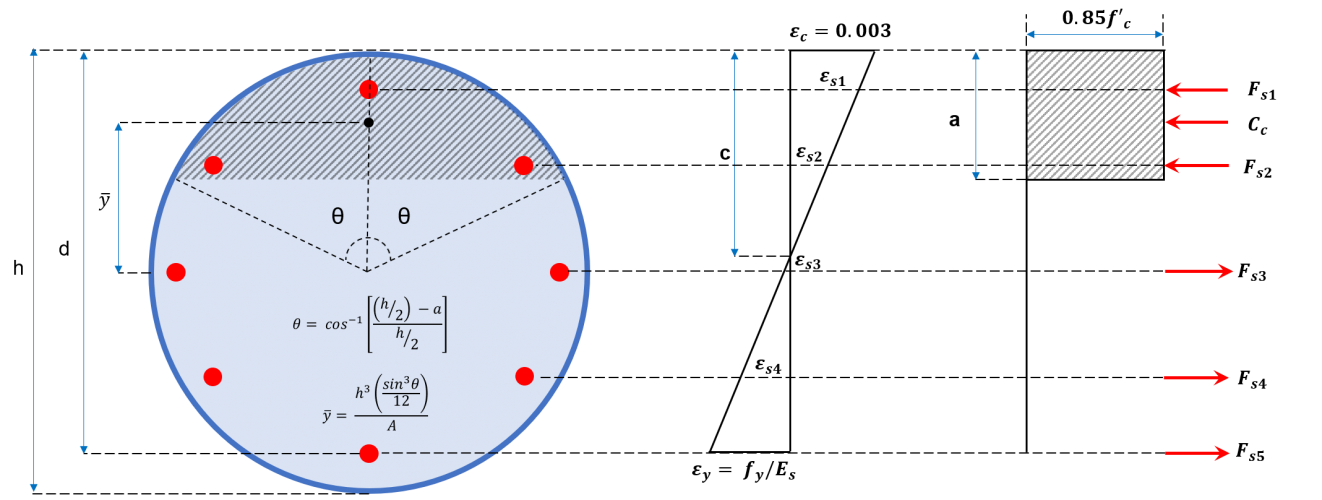
図2b: 円柱の断面

列の相互作用図の一般的な手順

(1) Pの値を計算します_の およびP_N (式8aおよび8b).

(2) cと鉄筋のひずみを決定します.

\( c = 0.003 [object Window]{{d}_{1}}{0.003 + (と + {e}_{そして})} \) (9)

c =中立軸の深さ

e_そして =鋼のひずみ= f_そして/E_s

Z =任意の値 (0, -0.5, -1.0, -2.5)

中立軸のさまざまな位置を選択することにより、一連のケースを検討する必要があります。, c. 中立軸の位置を設定するには, 鋼の降伏強度に任意の値Zを掛けることにより、異なる鋼ひずみを選択する必要があります。. Zにはさまざまな値があります. しかしながら, 相互作用図に使用する必須のポイントは4つだけです.

• Z = 0: この時点で, 張力の極限層でのひずみはゼロです. この点は、すべての縦棒で許可されている圧縮重ね継ぎから引張重ね継ぎへの変更を示しています。.
• Z = -0.5: このひずみ分布は、柱の引張り重ねスプライスの長さに影響します & 通常、相互作用図にプロットされます.
• Z = -1: これはバランスの取れた状態のポイントを示します. このひずみ分布は、セクションの圧縮面の押しつぶしによって発生する圧縮破壊から、縦方向の補強材の降伏によって開始される引張破壊への変化を示します。.
• Z = -2.5: この点は、の張力制御ひずみ限界に対応します。 0.005.

(3) 補強層の応力を計算します.

\({f}_{そして} ={e}_{そして} × {E}_{s} \) (10)

f_そして =鋼の応力

e_そして =鋼のひずみ

\({e}_{そして} = frac{c -{d}_{私}}{c} × 0.003 \) (11)

E_s =鋼の弾性係数

(4) 圧縮応力ブロックの高さを決定します, a.

\(a = {b}_{1} ×c \) (a≤h)(12)

f’c≤の場合 4000 psi (28 MPa):

b₁ = 0.85

f’cの場合 > 4000 psi (28 MPa):

\( {b}_{1} = 0.85 – \フラク{0.05 × (f’c – 4000)}{1000} \) (インペリアル)

\( {b}_{1} = 0.85 – \フラク{0.05 ×(f’c – 28)}{7} \) (メトリック)

(5) コンクリートと鋼の力を計算する.

圧縮応力ブロックの面積:

\({あ}_{c} = a×b \) (長方形の断面)

\({あ}_{c} ={h}^{2} [object Window]{θ – sinθcosθ}{4} \) (円形断面)

コンクリートの圧縮力:

\({C}_{c} = (0.85 ×f’c) × {あ}_{c}\) (14)

鋼の引張力 (d_私≤a):

\({F}_{そして} = {f}_{そして} × {あ}_{そして} \) (15)

鋼の圧縮力 (d_私 > a):

\({F}_{そして} = [{f}_{そして} – (0.85 ×f’c)] × {あ}_{そして} \) (16)

(6) 軸方向の容量を計算します (P_N).

\({P}_{N} = {C}_{c} + Σ {F}_{そして} \) (17)

(7) 曲げ能力を計算する (M_N).

\({M}_{N} = [{C}_{c} × (\フラク{h}{2} – \フラク{a}{2})]+ Σ [{F}_{そして} × (\フラク{h}{2} – {d}_{私}) \) (18)

(8) 強度低下係数の値を計算します (ø).

表に示すように 1, 軸方向とたわみの両方の強度低下係数は、 0.60 に 0.90. セクション 21.2 ACIの 318-14 今のところその価値を示しています, 軸力, またはモーメントと軸力の組み合わせ, 表に示すように 2 未満.

分類	螺旋	結ばれた
圧縮制御	0.75	0.65
圧縮から引張への移行	0.75 + [50 × (et – 0.003) ]	0.65 + [(250/3) × (et – 0.003) ]
張力制御	0.90	0.90

テーブル 2: 軸方向の強度低下係数, モーメントまたは軸とモーメントの組み合わせ (テーブル 21.2.2, ACI 318-14)

(9) 手順を繰り返します 2-8 Zのさまざまな値.

(10) øPの値を図にプロットします_N およびøM_N.

SkyCiv Free Foundation Calculatorを使用したコンクリートパイル設計

SkyCiv無料財団電卓 コンクリート杭の設計や、フーチングやコンクリート杭の設計などのその他の作業に役立ちます. 今すぐチェックして、当社の電卓がコンクリート杭プロジェクトにどのように役立つかを調べてください!

基礎設計計算機

参考文献

• • 構造コンクリートの建築基準要件 (2014). 交流! 318-14 アメリカコンクリート学会.
  • シャオ, J.K. (2012). 荷重モーメントに対する曲げ軸の影響 (P-M) 限られた数の縦方向鉄筋を使用した円形コンクリート柱の相互作用図. 構造工学の電子ジャーナル 12 (1). httpから取得://www.ejse.org