スチール接続設計, ボルト 通常、特定の荷重に抵抗する 1 つのボディとして機能するボルト グループとして設計されています。. ボルト グループの強度は通常、最も重要なボルトの強度を制御することによって計算されます。. 直接荷重はボルトの総数に分散されます, 一方、荷重の偏心によって誘発されるモーメントは、ボルトグループの慣性モーメントと重心からの距離に関連して分布します。. この分析は弾性分析と呼ばれます. 負荷分散に関する単純化された控えめな仮定のため, 過剰に設計されたボルト締結が生じることがよくあります.
バリューエンジニアリングと経済的な設計について話すとき, 非弾性的なアプローチは、ほとんどのメーカーに好まれています. 同じ大きさの荷重に対して必要なボルトの数が少なくて済みます. 非弾性アプローチを行うには, 瞬間回転中心 (ICOR) 反復を使用する方法が最善の方法です.
記事上で, の強度を計算する方法を説明します。 ボルト接続 ICOR メソッドを使用する. ボルトあたりの反応は、式を使用して計算されます (7-1) ページ上 7-7 の AISC 第 15 版マニュアル. これを使用して、ボルト グループの瞬間的な中心の想定位置が正しいかどうかを確認します。. 最後に, 正しい IC の位置がわかったら, 次に、ボルト グループ係数 C を計算して、その強度を決定します。.
ボルト グループ係数を取得する際の ICOR メソッドの使用は、瞬間中心を取得する試行錯誤の方法が必要なため、長いプロセスになります。 (IC) ロケーション. 今日では, コンピュータソルバーを使用して, ボルト グループの IC は、プログラムされた反復を使用して簡単に計算できます。. SkyCiv ボルト グループ ソルバー 高速反復法を使用して、IC の位置とボルト グループの係数をわずか数秒で決定します. 現在、AS に実装されています。 4100 設計コードですが、すぐに残りの設計コードに統合される予定です.
ボルト グループ プロパティの取得
偏心垂直せん断荷重が負荷された 4 本のボルトからなるボルト グループで簡単な解析を開始しましょう。 10 キップ. x軸に沿った負荷の偏心は 4 ボルトグループの右側にインチ. 垂直からの角度はゼロ、y 軸に沿った偏心はゼロです。.
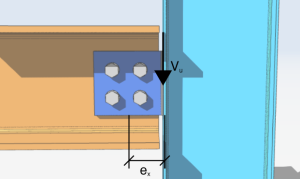
\(V_{あなた} = 10キップ \)
\(\シータ = 0 度)
\(e_{バツ} = 4 の)
\(e_{そして} = 0インチ)
最初に行うことは、ボルト グループ内のすべてのボルトの座標を取得することです。. 視覚的なガイドと表の使用を強くお勧めします.
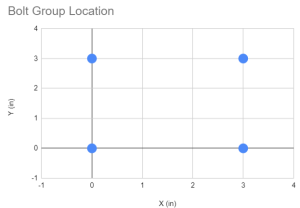
| 店舗ID | バツ (に) | そして (に) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
x に沿ってボルト グループの重心を取得するには- およびy軸, 以下の式が必要です.
させて \(ん \) = ボルトの総数
\(バツ_{CG} = frac{\合計 X}{ん}\)
\(Y_{CG} = frac{\合計 Y}{ん} \)
その後, 私たちのソリューションは:
\(バツ_{CG} = frac{\合計 X}{ん} = frac{0 に + 0 に + 3 に + 3 に}{4} = 1.5 の)
\(Y_{CG} = frac{\合計 Y}{ん} = frac{0 に + 3 に + 0 に + 3 に}{4} = 1.5 の)
I.Cの位置を想定する.
重心を取得した後, 瞬間的な中心の位置を仮定します \(IC). 最初の試みとして, IC はボルト グループの幾何学的重心にあると想定できます。.
そう, 推定
\(バツ_{IC} = X_{CG} = 1.5 の)
\(Y_{IC} = Y_{CG} = 1.5 の)
その後, ICの位置までの各ボルトの変位を表にします. これは、最初に x に沿った距離と y に沿った距離を取得することで簡単に実行できます。, 次に、その変位を取得します
| 店舗ID | cx (に) | サイ (に) | c (に) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
どこ,
\(c_{バツ} = X_{私} – バツ_{IC}\)
\(c_{そして} = Y_{私} – Y_{IC}\)
\(c = sqrt{{\左(c_{バツ} \正しい)}^{2} + {\左(c_{そして} \正しい)}^{2}}\)
ボルトNo用. 1, 私たちのソリューションは
\(c_{バツ} = 0インチ – 1.5 =で -1.5 の)
\(c_{そして} = 0インチ – 1.5 =で -1.5 の)
\(c = sqrt{{\左( -1.5 right で)}^{2} + {\左( -1.5 right で)}^{2}} = 2.121in\)
ICからの距離に対するボルト1本当たりの変形量を計算
したがって, 想定される IC 位置からのボルト距離を取得した後, 次に、各ボルトの変形をその距離の関数として計算します.
ボルトあたりの最大変形量, に設定 \(\デルタ_{最高} = 0.34 の), AISC ページに記載されている ASTM ボルトの実験データに基づいています。 7-8. 線形比例を使用して, と設定 \(\デルタ_{最高} = 0.34 の), 最大距離までの部分に対する個々のボルトの変形を計算できます \(c_{最高}\). 取得の式 以下に示す.
\(\デルタ_{1} = 0.34in times left( \フラク{c}{c_{最高}}\正しい) \)
ボルトNo用. 1, 変形は
\(\デルタ_{1} = 0.34in times left( \フラク{2.121 に}{2.121 に}\正しい)\)
残りのボルトについて, 計算された変形を以下に表にします.
| 店舗ID | \(\Delta\) (に) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
ボルトごとの反応を取得する
ボルトごとの変形が得られたら, その後、AISC 15th Ed を使用できます. Eq (7-1) ボルトごとの反応を取得する.
\(R = R_{圧縮力の合計が引張力と等しくない間、上記の手順が繰り返されます} \左 ( 1 – e ^{-10\デルタ}\正しい )^{0.55}\)
の \(R_{圧縮力の合計が引張力と等しくない間、上記の手順が繰り返されます}\) 式の は、ボルトにかかる想定される最終荷重です。, これをボルトのせん断強度として設定できます.
\(R_{圧縮力の合計が引張力と等しくない間、上記の手順が繰り返されます} = phi R_{ん} \)
私たちの例では, のボルトせん断強度を使用します。 \(24.4 キップ). 別の値を使用することもできます。これは、ボルト グループ係数を計算するときに相殺されるためです。 \(C) 後で.
ボルトNo用. 1, 計算された反応は
\(R = R_{圧縮力の合計が引張力と等しくない間、上記の手順が繰り返されます} \左 ( 1 – e ^{-10\デルタ}\正しい )^{0.55}\)
\(R = 24.4 キップ左 ( 1 – e ^{-10 \倍左 ( 0.34 right で )}\正しい )^{0.55}\)
\(R = 23.949 キップ)
残りのボルトについて, 計算された反応は次のとおりです。. 同時に, ボルト反力の成分 \(R ) x と y に沿って表示されます.
| 店舗ID | R (キップ) | 処方箋 (キップ) | ライ (キップ) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
ボルトNo.1用, x および y コンポーネントを取得するためのソリューションを以下に示します。.
\(R_{バツ} = -R 左 ( \フラク{c_{そして}}{c} \正しい ) = -23.949 \倍左 ( \フラク{-1.5に}{2.121に} \正しい ) = 23.949 キップ)
\(R_{そして} = R 左 ( \フラク{c_{バツ}}{c} \正しい ) = 23.949 \倍左 ( \フラク{1.5に}{2.121に} \正しい ) = 23.949 キップ)
しかも, 偏心によるボルトごとの誘導モーメント荷重を取得する必要があります. これを計算するには, コンポーネントを使用します \(R_{バツ}\) そして \(R_{そして}\) それらに偏心率を掛けます \(c_{そして}\) そして \(c_{バツ}\), それぞれ.
ボルトNo.1用, ICが反応した瞬間
\(M_{r} = -R_{バツ}c_{そして} + -R_{そして}c_{バツ} \)
\(M_{r} = -16.937 kip times left ( -1.5right で) + -16.937 kip times left ( -1.5 right で ) \)
\(M_{r} = 50.811 チキンイン)
残りのボルトについて, 対応するモーメント反応を以下に表にします.
| 店舗ID | 氏 (チキンイン) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀さん= 101.622 |
IC の場所の確認
ボルトごとのせん断反力とモーメント反力が得られたので、, これを使用して、このボルト グループが抵抗する Pu 負荷の量を決定します。. これをする, x に沿ったすべての反応の合計と y に沿ったすべての反応の合計の結果を取得します。.
前のセクションから, 私たちはそれを計算しました
\(\合計R_{バツ}=0kip\)
そして
\(\合計R_{そして}=0kip\)
そう,
\(P_{あなた} = sqrt{{\左( \合計R_{バツ} \正しい)}^{2} + {\左( \合計R_{そして} \正しい)}^{2}} = 0 キップ)
結果として生じる負荷から \(P_{あなた} = 0kip), この時点で、データがゼロになるため、検証を続行しないことを決定できます. また、最初に想定された I.C. の位置を推測することもできます。, ボルトグループの重心にある, 間違っています. しかしながら, この議論の目的のために, 以下の手順に進みます.
\(P_{ux} = -P_{あなた}罪左 ( \シータ右 ) = 0 キップ \)
\(P_{あなた} = -P_{あなた}cos左 ( \シータ右 ) = 0 キップ \)
\(M_{あなた} = -P_{ux}\左 ( Y_{CG} + e_{そして} – Y_{IC} \正しい ) + -P_{あなた} \左 (バツ_{CG} + e_{バツ} – バツ_{IC} \正しい ) = 0 キップ \)
以来,
\(P_{ux} \neq sum R_{バツ} \)
\(P_{あなた} \neq sum R_{そして} \)
\(M_{あなた} \私はM_ではありません{r} \)
したがって, I.Cの想定位置. 間違っています. これで、次の想定される場所に進むことができます.
SkyCiv はボルト グループ計算をオーストラリア標準モジュールに完全に統合しています. 当社の接続設計ソフトウェアを試してみたい?
2 回目の繰り返し
2回目の反復, I.C. 以下に示す座標にあります.
推定
\(バツ_{IC} = 0.062 の)
\(Y_{IC} = 1.5 の)
その後, 最初の反復で行った手順を実行しましょう. 要約すれば, 下の表は座標を示します, 想定される I.C からの各ボルトの距離, および距離に関する対応する変形.
| 店舗ID | バツ (に) | そして (に) | cx (に) | サイ (に) | c (に) | \(\Delta\) (に) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
計算された重心は、 ボルトグループ ボルト座標は何も変わっていないので、同じままです.
\(バツ_{CG} = 1.5 の)
\(Y_{CG} = 1.5 の)
その後, xに沿って反応を計算します, y に沿った反応, そして対応する瞬間. 値を以下に表にします.
| 店舗ID | R (キップ) | 処方箋 (キップ) | ライ (キップ) | 氏 (チキンイン) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀さん= 222 |
次, x と y に沿ったすべての反応の合成負荷を決定します。.
\(P_{あなた} = sqrt{{\左( \合計R_{バツ} \正しい)}^{2} + {\左( \合計R_{そして} \正しい)}^{2}}\)
\(P_{あなた} = sqrt{{\左( 0 キップ右)}^{2} + {\左( 40.703 キップ右)}^{2}}\)
\(P_{あなた} = 40.703 キップ)
その後, 与えられた荷重に基づく合力荷重の成分 \(\theta ) 以下に示す.
\(P_{ux} = -P_{あなた}罪左 ( \シータ右 ) = -41kip times sin left ( 0 度右 )= 0 キップ)
\(P_{あなた} = -P_{あなた}cos左 ( \シータ右 ) = -41kip times cos left ( 0 度右 )= -41 キップ)
次に、これらのコンポーネントを使用して、想定される I.C に関するモーメント荷重を解決します。.
\(M_{あなた} = -P_{ux} \左 ( Y_{CG} + e_{そして} – Y_{IC} \正しい) + P_{あなた} \左 ( バツ_{CG} + e_{バツ} – バツ_{IC} \正しい)\)
\(M_{あなた} = -0 キップ左 ( 1.5 に +0 に – 1.5 right で) + 41 キップ左 ( 1.5 に +4 に – 0.06 right で)\)
\(M_{あなた} = -222 チキンイン)
次, 計算して比較してみましょう Pux, Pux, そして Mあなた ボルトグループの反応に.
\(P_{ux} \約 – \合計R_{バツ}\)
\(P_{あなた} \約 – \合計R_{そして}\)
\(M_{あなた} \約 – \合計 M_{あなた}\)
式の左辺と右辺はほぼ等しいので、, I.Cの想定位置と言えます。. 正しい!
C係数の解法
I.Cになったら. 場所が決まる, 以下の式でボルト グループ係数 C を取得できます。.
\(C = frac{P_{あなた}}{\ファイR_{ん}} = \frac{40.703 キップ}{24.4 キップ} = 1.668\)
フリーボルトグループ計算機
このアプローチでボルト締結をどのように設計するかを確認してください。 無料の鉄骨接続設計電卓! より多くの機能を使用するには, 今すぐ Structural 3D ソフトウェアにサインアップして開始してください!


