周波数分析の定義?
建物を設計するとき, 二つあります 荷重の種類 考慮する: 静的および動的. 最初のもののために, 変位と応力に関して適用される永久荷重に対する構造の直接応答を計算することだけが必要です。. これは、剛性または有限要素法を使用して達成できます。.
動的解析の場合, 時間依存の荷重による構造の応答の可能な変動の範囲を考慮することは、より困難です。. したがって, いくつかの新しいツールまたは機能を分析に含めることが不可欠になります. そう, 周波数分析, 振動力学における基本的な方法, 発生する.
この方法は、加えられた動的荷重による構造物の運動の時間変化を取得します。. すなわち, これは、構造システムの振動の自然な特性を使用して内力を計算することを意味します。, 変位, 安定性の問題, 等.
トピックの詳細については, 実行方法を簡単に説明するSkyCivの記事を読むことをお勧めします 動的周波数分析 を使用して SkyCiv構造解析ソフトウェア.
周波数解析が設計に関係する理由?
設計における周波数解析の重要性を測る最良の方法は、悪い動的挙動のために失敗したいくつかの構造のケースを観察することです. 北米で有名な橋の 1 つは、タコマ ナロウズです。, 風によって引き起こされた持続的な周期的な振動の後、最終的に崩壊しました. 次の画像は、崩壊直前の橋に沿った変位の増加を示しています。, 主に車道を中心に:

図 i. Tacoma Narrows 橋の横ねじり振動

図Ⅱ. 崩壊前の橋の変位の増加.

図ⅲ. 壊滅的な橋の崩壊
このケーススタディでは, 適切な周波数解析が実行されておらず、構造の固有振動数を考慮するように構造が適切に設計されていませんでした。.
単純な振り子
周波数分析は、構造が外部の動的作用を受けたときに構造が発達するさまざまな形態を研究します。. これが、いくつかの異なるものを取得する理由です モード. 次に、これらのフォームを使用して, 平衡を保証するために必要な内力によって、構造の要素サイズを確立できます。.
周波数解析の技術的および数学的考慮事項に入る前に, 図 iv に示す振り子柱の次の単純なシステムを確認してください。.
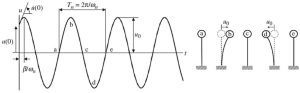
図iv. 自由振動振り子システムの動的応答
最後の画像に示されているように、単純な分析を使用する, 振り子柱の上部質量の動きを毎回定義できます. この記事の主な目的は、2 つの典型的なケースの周波数分析をカバーすることです。, 単一および複数の自由度.
単一の自由度
この特定のケースは、動的分析にとって最も単純です. この動作は、ダランベールの平衡法則を使用して記述されます, 第 2 ニュートンの法則の拡張.
次の図は、SDOF システムの要素を示しています。, 剛性 (k), ダンピング (c), と質量源 (メートル) 慣性力用. 質量に加えられる時間変化する外力は、次のように表されます。 \({p(t)}\).
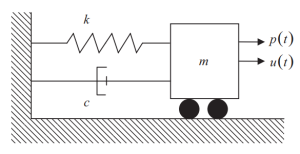
図 1. 単一の自由度 (SDOF) システム. (丼鉢, 2017, ページ 56)
すべての要素が動的平衡条件を満たす必要があります:
\({メートル}{\ドット{あなた}}+{c}{\ドット{あなた}}+{k}{あなた}={p(t)}\)
これは線形 2 階微分方程式です。, そのソリューションには2つのコンポーネントがあります:
\({あなた(t)}={あなた}_{h}(t)+{あなた}_{p}(t)\)
どこ:
- \({あなた(t)}\) は絶対変位です.
- \({あなた}_{h}(t)\) は同次解です, 一般的に自由振動ケースを含む.
- \({あなた}_{p}(t)\) 適用される励起に応じた特定のソリューション.
振動挙動と構造物が持つ最も重要な動的特性を説明するために、均一なソリューションのみに焦点を当てます。.
次の用語を定義しましょう:
\({\オメガ_{ん}}={\平方根(\フラク {k}{メートル})}\) 角周波数
\({\xi}={\フラク{c}{{2}{メートル}{\omega_n}}}={\フラク{c}{{2}{\平方根(\フラク {k}{メートル})}}}\) 臨界減衰率
臨界減衰の割合が以下の場合 1, 振動ケースは減衰不足になります; あれは, モーションが停止する前に完了したサイクルがあります.
解は次の一般的な形式です
\({u_h}={e ^{{-\xi}{\オメガ_{ん}}{t}}}{[{あ}{cos}{\omega_d}{t}+{B}{それなし}{\omega_d}{t}]}\)
どこ:
- A と B は運動の初期条件に依存する積分定数です。.
- \({\omega_d}={\omega_n}{\平方根({{1}-{\xi^2}})}\) は減衰角周波数
A 定数と B 定数の評価後, 減衰しない場合の一般的な解は、
\({u_h}={e ^{{-\xi}{\オメガ_{ん}}{t}}}{[{u_0}{cos}{\omega_d}{t}+{\フラク{{\ドット{u_0}}+{\xi}{\omega_n}{u_0}}{\omega_d}}{それなし}{\omega_d}{t}]}\)
どこ:
- \({u_0}\) は質量の初期変位です
- \(\ドット{u_0}\) は質量初速度
初期条件のいくつかの値で解をプロットすると, 次の図が得られます.
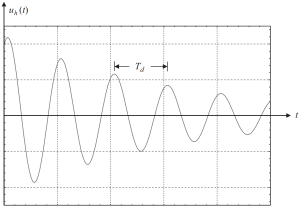
図 2. 変位は、亜臨界減衰の場合に解の均一な部分をもたらします. (丼鉢, 2017, ページ 58)
それ以外の場合, 臨界減衰の一部の値が 1. \({\xi}=1). この条件は、完全な減衰を持つ構造を意味します.
使用する方程式は
\({u_h}={e ^{{-\オメガ_{ん}}{t}}}{\{u_0+({\ドット{u_0}}+{\omega_n}{u_0}){t}}\}\)
そして、初期条件のさまざまなケースを示すグラフは、次の画像にあります.
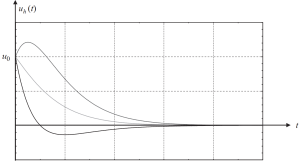
図 3. 変位は、臨界的に減衰した場合に解の均一な部分をもたらします. (丼鉢, 2017, ページ 58)
応答パラメータ
前のセクションは、SDOF システムにおける自由動的振動のソリューションを定義するのに役立ちました。. 2 つの主なパラメータは固有振動数です \(\omega_n) これは、構造がそれ自体でどのように振動するかを示します, および臨界減衰の割合 \(\xi), 減衰振動の速度を定義します.
一般的に, 構造物は減衰が低く、最大値は \(\xi)=10 %. この値を用いて減衰固有振動数を評価すると, 結果は \({\omega_d}=0.995{\omega_n}\). そう, 使用することをお勧めします \({\omega_d}{\厚い近似}{\omega_n}\).
次の表に動的プロパティをまとめます。.
| 角周波数 (ラジアン/秒) | 固有振動数 (Hz) | 自然周期 (s) | |
|---|---|---|---|
| 角周波数 \({\omega_n}\) | \({\omega_n}\) | \(2{\パイ}{f_n}\) | \(\フラク{2{\パイ}}{T_n}\) |
| 固有振動数 \({f_n}\) | \(\フラク{\omega_n}{2{\パイ}}\) | \(f_n\) | \(\フラク{1}{T_n}\) |
| 自然周期 \({T_n}\) | \(\フラク{2{\パイ}}{\omega_n}\) | \(\フラク{1}{f_n}\) | \(T_n\) |
テーブル 1. 角周波数の関係, 固有振動数, と期間 (丼鉢, 2017, ページ 60)
複数の自由度
構造物に多くの塊が存在する場合, これらの質量の位置をいつでも記述するために、複数の座標を定義する必要があります. 次の図に、特定の明らかな例を 1 つ示します。, 運動のあらゆる瞬間に位置を確立するために異なる角度が必要な複雑な振り子からなる.
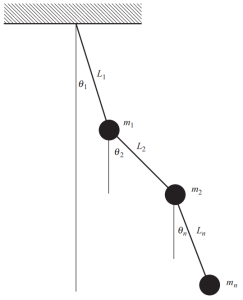
図 4. 複数の質量を持つ振り子. (丼鉢, 2017, ページ 53)
このセクションで, 構造を分析します’ 特性の拡張を使用した一般的な動的応答 多自由度の周波数解析.
実際の構造を扱うときは、モデリング プロセスを認識することが不可欠です。. 次の図は、周波数解析を適用して動的応答を記述する準備が整った数学的モデルを構築するために必要な手順を示しています。.
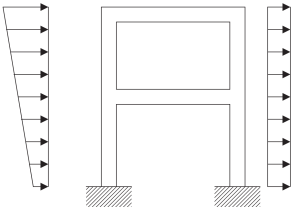
図 5. 連続構造フレームの物理モデル. (丼鉢, 2017, ページ 23)
最初のステップでは、梁と柱のすべてのレベルの交点で質量を集中させます. 各ノードには 3 つの可能な動きがあります, 2 つの線形変位, そして一回転. 分析に一貫性を持たせる, 質量と極慣性特性を考慮する必要があります.
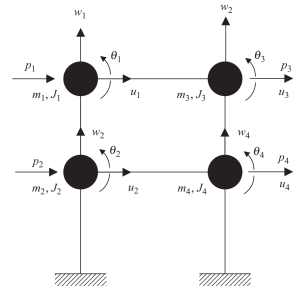
図 6. 変位と回転の自由度を持つ節点での集中質量. ディスクリート システム. (丼鉢, 2017, ページ 23)
静的凝縮法は、分析の複雑さを軽減するのに役立ちます, 回転慣性と並進慣性を無視.
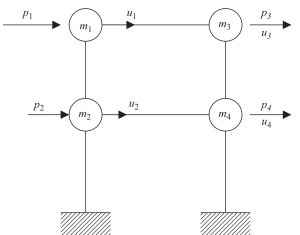
図 7. 自由度を水平移動のみに静的に凝縮. (丼鉢, 2017, ページ 23)
最後のステップで, このフレームの例では、水平方向の動きを 2 つのノードだけにまとめることができます.
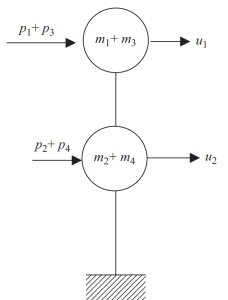
図 8. 2 つのノードへの最終的な静的凝縮と水平変位の自由度. (丼鉢, 2017, ページ 24)
前のセクションで SDOF システムで行ったように, 多自由度の運動方程式の解を開発します.
運動方程式は、行列形式で次のように記述します。
\([M]\{\ドット{あなた}\} + [C]\{\ドット{あなた}\}+[K]\{あなた}={p(t)}\)
どこ:
- \([M]\) は質量行列です
- \([C]\) クーラムの減衰行列
- \([K]\) それは 剛性マトリックス
応答パラメータを取得するには、自由振動解を調べる必要があります。. システムに適用されるダンピングと力はありません, 評価される初期条件のみ.
\([M]\{\ドット{あなた}\} +[K]\{あなた}={0}\)
SDOF の最初のケースと同様に, 次の形式の正弦波解をテストできます.
\({あなた(t)}={\ファイ}{({a}{cos}{\オメガ}{t}+{b}{それなし}{\オメガ}{t})}\)
\({\ドット{あなた}{(t)}}={-{\オメガ}^ 2}{\ファイ}{({a}{cos}{\オメガ}{t}+{b}{それなし}{\オメガ}{t})}\)
ベクトル \(\ファイ) は時間に依存しない形状ベクトルです. 係数 “a” そして “b” 初期条件を評価するときに得られる定数です.
テスト解の両方の式を運動方程式に代入した後, 線形固有値-固有ベクトル問題を取得します:
\([K]{\ファイ}={{\オメガ}^ 2}[M]{\ファイ}\)
どこ:
- \({{\オメガ}^ 2}\) は固有値のセットです
- \({\ファイ}\) は固有ベクトルの集合です
最新の図のフレーム例のこの古典的な問題の解決策は、質量がどのように振動するかを示しています. これは、すべての質量が固有ベクトルの値に従って水平方向に移動することを意味します.
この動作の次の画像を見てください.
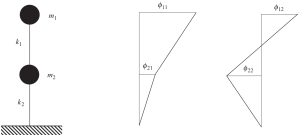
Figure No.9. 2 つの固有ベクトルの結果を示す周波数分析. (丼鉢, 2017, ページ 135)
SkyCiv構造3D
で構造の周波数解析を実行します SkyCiv構造3D. 今すぐサインアップして始めましょう!
参考文献:
- エドゥアルド・カウセル, (2017). “高度な構造力学” 1初版, ケンブリッジ大学出版局


