NBCC の完全に機能した例 2015 積雪荷重計算

構造物に積もった雪は、屋根のメンバーやその他の露出した構造要素にとって非常に危険です。. の カナダの建築基準法 (2015) ディビジョンB – セクション 4.1.6 雪の負荷と関連する雨の負荷の詳細な計算を提供します. このガイドラインの使用, 構造 3D の例を使用して、積雪荷重を計算する方法を実演します。 (S3D) 倉庫モデル, 以下に示すように:

図 1: S3D 倉庫モデルの例

図 2: Google マップを使用したサイトの場所の例 (説明のみ).

テーブル 1: 積雪荷重計算に必要な建物データ.

ロケーション	オグデン, カルガリー, アルバータ州 (説明のみ)
占有	材料の倉庫または保管
外形寸法	19.508 m × 31.70 各構造の m 小さい建物の軒高 9.144 メートル 小さい建物の頂点の高さ 11.941 メートル 上下の屋根の違いは 3.50 メートル 屋根ピッチ角 16°
追加の詳細	屋根の表面が滑りやすい 構造間のギャップは 2.30 メートル

テーブルから 1, 指定された積雪荷重, \(S ), 式を使用して計算できます:

\(S = {私}_{s}[{S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{a} +{S}_{r}]\) (1)

どこ:

\({私}_{s}\) = 積雪荷重の重要度, 表 4.1.6.2-A
\({S}_{s}\) = 1-50 年間の地上積雪荷重, kPa, サブセクション 1.1.3
\({C}_{b}\) = 基本的な屋根の積雪負荷率, 4.1.6.2 (2)
\({C}_{w}\) = 風曝露係数に基づく, 4.1.6.2 (3) そして (4)
\({C}_{s}\) = 勾配係数, 4.1.6.2 (5), (6), そして (7)
\({C}_{a}\) = 累積係数, 4.1.6.2 (8)
\({S}_{r}\) = 50 年に 1 回の関連する降雨量, kPa, サブセクション 1.1.3, より大きくない \({S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{a}\)

各パラメータは、次のセクションで個別に検討されます。. 次の積雪荷重ケースが計算されます: 各屋根の積雪荷重のバランスとアンバランス (尾根に垂直な風), 滑りによる蓄積を考慮したロアルーフに発生するドリフト.

重要度, \({私}_{s}\)

最初に決定されるのは重要度の要素です, \({私}_{s}\), を使用して見つかります 表 4.1.6.2-A 参照として. 構造物が万一の故障時に人命への直接的な影響が少ない貯蔵庫であるため, 重要度のカテゴリは 低. しかも, 計算はUltimate Limit状態になります (ULS). だからから 表 4.1.6.2-A, \({私}_{s}\) に等しい 0.80.

重要性カテゴリー	重要度, \({私}_{s}\)
	ULS	SLS
低	0.8	0.9
正常	1.0	0.9
高い	1.15	0.9
災害後	1.25	0.9

地面雪荷重, \({S}_{s}\), および関連する降雨荷重, \(({S}_{r})\)

地積雪荷重, \({S}_{s}\), および関連する降雨荷重, \(({S}_{r})\), 値は表に示されています 付録C, NBCCのディビジョンB 2015 場所や都道府県にもよる. この例では, 対応します \({S}_{s}\) そして \(({S}_{r})\) に カルガリー アルバータ州 に等しい 1.10 kPa そして 0.1 kPa, それぞれ.

NBCC では、地面の雪とそれに伴う降雨量を探すのに苦労しています。 2015? 試す の SkyCiv 無料ロード ジェネレーター ツール 検索を高速化し、対応する \({S}_{s}\) そして \({S}_{r}\) あなたの構造の場所に基づいて.

SkyCiv雪負荷計算機

風露出係数, \({C}_{w}\)

風曝露係数について, \({C}_{w}\), と等しいことが許されます 1.0 に基づく 4.1.6.2 (3). の条件が満たされている限り、この要因はまだ削減できます。 4.1.6.2 (4) 満足しています. この例では, \({C}_{w}\) に等しいものとする 1.0 場所が構造物を完全に風にさらすような開けた地形ではないため.

基本的な屋根雪負荷係数, \({C}_{b}\)

基本屋根積雪負荷率, \({C}_{b}\), 次の式を使用して計算できます, で参照されているように 4.1.6.2 (2):

\({C}_{b} = 0.8\) (2) ために \({l}_{c} ≤ (70/{{C}_{w}}^{2})\) そして
\({C}_{b} = (1/{C}_{w}) [1 – (1 – 0.8{C}_{w})経験値(-0.01({l}_{c}{{C}_{w}}^{2} – 70))] \) (3) ために \({l}_{c} > (70/{{C}_{w}}^{2})\)

どこ:

\({l}_{c}\) = として定義される上部または下部の屋根の特性長: \(2w -{w}^{2}/l)
\(l) = 屋根のより大きな平面寸法
\(w) = 屋根の小さい平面寸法

この例では,\(l) そして \(w) に等しい 31.7 mと 19.51 メートル, それぞれ, したがって, \({l}_{c}\) に等しい 27.01. 以来 \({l}_{c}\) よりも少ない \((70/{1.0}^{2})\), 屋根の基本積雪負荷率, \({C}_{b}\), に等しい 0.8.

勾配係数, \({C}_{s}\)

勾配係数の計算は次のとおりです。 \({C}_{s}\) 詳細に 4.1.6.2 (5), (6), そして (7) 以下に示す.

遮るもののない滑りやすい屋根用:

\({C}_{s} = 1.0\) ために \(α ≤ 15°\)
\({C}_{s} = 0\) ために \(a > 60°\)
\({C}_{s} = (60° – a)/45°\) ために \(15° < α ≤ 60°\)

その他の場合:

\({C}_{s} = 1.0\) ために \(α ≤ 30°\)
\({C}_{s} = 0\) ために \(a > 70°\)
\({C}_{s} = (70° – a)/40°\) ために \(30° < α ≤ 70°\)

雪の比重, \(γ\)

雪の比重は、 4.1.6.13 とみなされます:

\(γ = 0.43{S}_{s} + 2.2 kN/{メートル}^{3} ≤4.0kN/{メートル}^{3}\) (4)

この例では, \(γ\) に等しい \(2.673 kN/{メートル}^{3}\).

累積係数, \({C}_{a}\)

累積係数, \({C}_{a}\), l l 4.1.6.2 (8). l .

指定積雪荷重, \(S )

このセクションで, 指定雪荷重, \(S ), バランスとドリフトの場合について計算されます.

バランス/ドリフトのないケース

バランス・ノンリフトの場合, の 累積係数 \({C}_{a}\) に等しい 1.0. しかも, l \(α\) です \(16°\) 屋根の表面は障害物がなく滑りやすいと想定されます, 勾配係数, \({C}_{s}\), 私たちの例では 0.978. 方程式の使用 (1), 指定された積雪荷重, \(S ), バランス型/リフトなしの場合は:

\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa

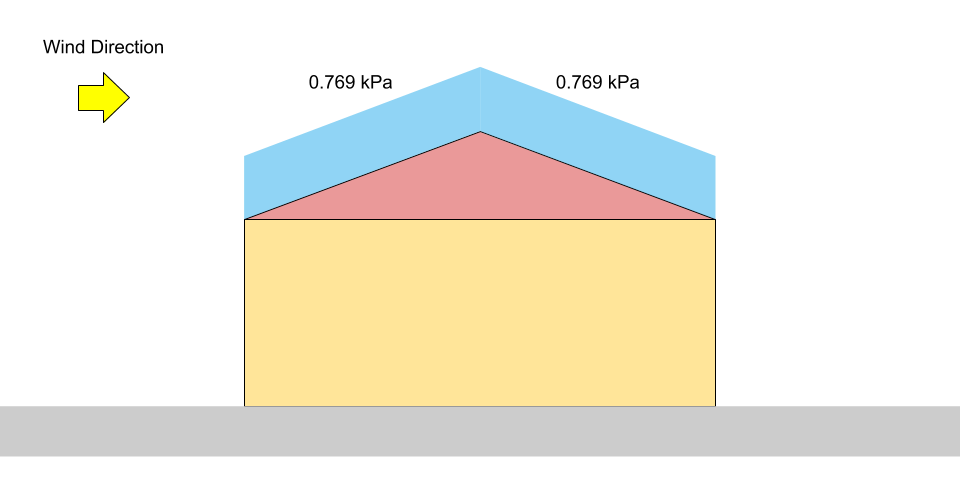
図 3: 切妻屋根の積雪荷重のバランス荷重図.

アンバランス・ドリフトケース

尾根に垂直に作用する風

建物は切妻屋根なので, アンバランスな積雪 (尾根に垂直に作用する風) 累積係数 \({C}_{a}\) を使用して見つかります 4.1.6.9:

\({C}_{a, 風上} = 0\)
\({C}_{a, 風下} = 0.25 +α/20\) ために \(15° ≤ α ≤ 20°\)
\({C}_{a, 風下} = 1.25\) ために \(20° < α ≤ 90°\)

両方の構造の屋根のピッチ角が 16° に等しいため, 累積係数 \({C}_{a, 風上}\) そして \({C}_{a, 風下}\) 等しい 0 そして 1.05, それぞれ. しかも, l \(α\) です \(16°\) 屋根の表面は障害物がなく滑りやすいと想定されます, 勾配係数, \({C}_{s}\), 私たちの例では 0.978.

リッジに垂直なアンバランス/ドリフトの場合, \({C}_{a}\) に基づいて計算されます 4.1.6.9 切妻屋根の場合. 上記の計算から, \({C}_{a, 風上} = 0\) そして \({C}_{a, 風下} = 1.05\). したがって, 各側の指定雪荷重は:

\({S}_{風上} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S}_{風下} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)

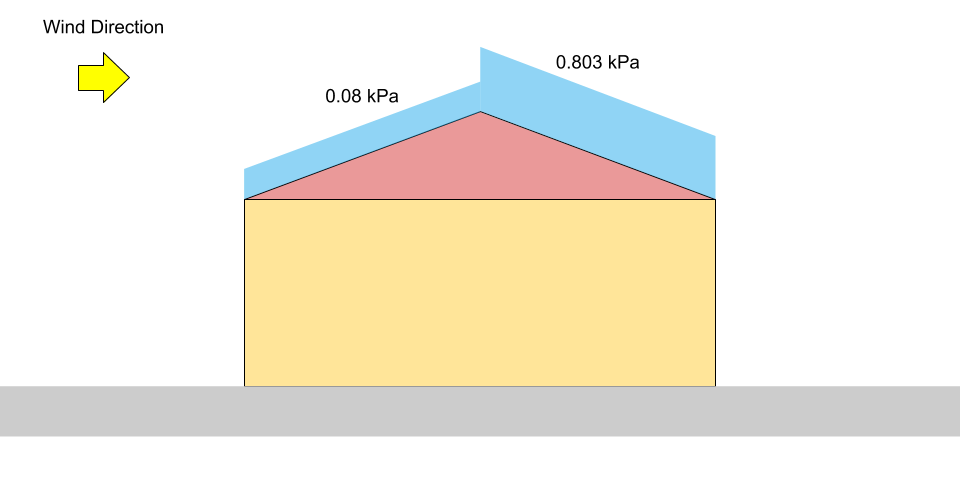
図 4: 切妻屋根の不均衡な積雪荷重の荷重図 (スケールしない).

尾根に平行な風の作用 – ケースⅠ – 上から下への風

尾根と平行に風が吹いているとき, 吹きだまりが下部の屋根に発生する可能性が最も高い. l 累積係数 \({C}_{a}\), から次の式 4.1.6.2 (8) 使用されています:

\({C}_{a} ={C}_{a0} – ({C}_{a0} – 1)(バツ/{バツ}_{d})\) ために \(0 ≤x≤ {バツ}_{d}\)
\({C}_{a} = 1.0\) ために \(バツ > {バツ}_{d}\)

どこ:

\({C}_{a0}\) = のピーク値 \({C}_{a0}\) x = 0
\(バツ) = ルーフステップからの距離
\({バツ}_{d}\) = 図に示すドリフトの長さ 3 未満

図 5: 屋根寸法パラメータの図

 

図 6: に基づくロアルーフの対応ドリフト荷重 図 4.1.6.5-A.

\({C}_{a0}\) そして \({バツ}_{d}\) 次の式を使用して計算できます:

\({C}_{a0} = frac{βγh}{{C}_{b}{S}_{s}}\) または \({C}_{a0} = frac{F}{{C}_{b}}\) (5), どちらか少ない方

\({バツ}_{d} = 5 \フラク{{C}_{b}{S}_{s}}{c}({C}_{a0} – 1)\) (6)

\(F = 0.35β\sqrt{\フラク{c({l}_{cs} – 5{{h}_{p}}^{」})}{{S}_{s}}} +{C}_{b}\) だが \(F ≤ 5\) ために \({C}_{ws} = 1.0\) (7)

\({h}^{」} = h – \フラク{{C}_{b}{C}_{w}{S}_{s}}{c}\) (8)

\({{h}_{p}}^{」} ={h}_{p} – \フラク{0.8{S}_{s}}{c}\) だが \(0 ≤ {{h}_{p}}^{」} ≤ \frac{{l}_{cs}}{5}\) (9)

どこ:

\({h}_{p}\) = 上部屋根の欄干の高さ (0 この場合、欄干がないので)
\(h ) = 屋根の上下の高さの差
\({C}_{ws}\) =の値 \({C}_{w}\) ドリフトの発生源に適用
\({l}_{cs}\) = として定義されるソース領域の特性長: \(2{w}_{s} -{{w}_{s}}^{2}/{l}_{s}\)
\({l}_{s}\) = 図に示すように、ソース領域のより大きな平面寸法 7 そして 8, 下に示された
\({w}_{s}\) = 図に示すように、ソース領域のより小さな平面寸法 7 そして 8, 下に示された
\(β\) = 1.0 ケースⅠの場合, そして 0.67 ケース II および III の場合.

 

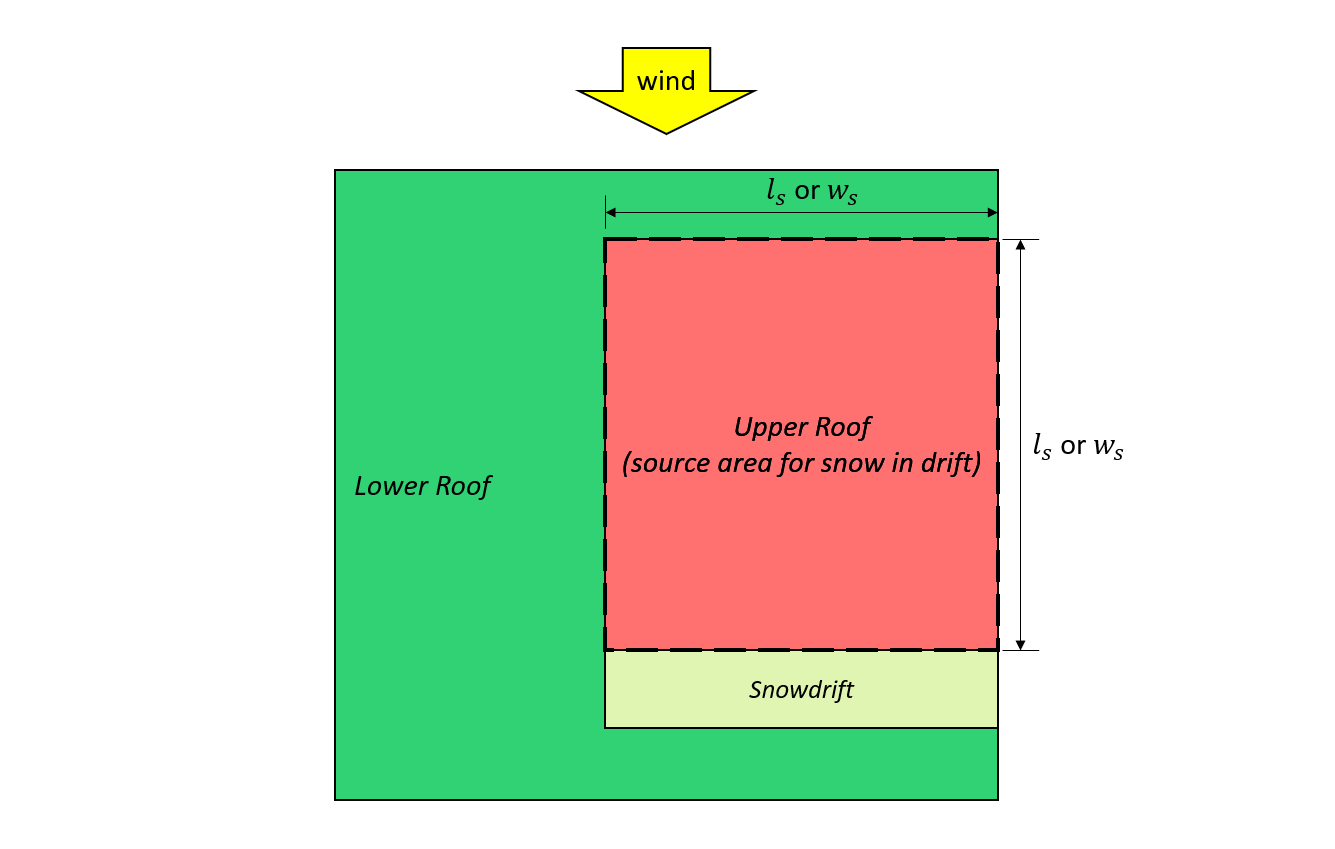
図 7: ケースⅠ – 上屋根から吹く風でできた吹きだまり 図 4.1.6.5-B.

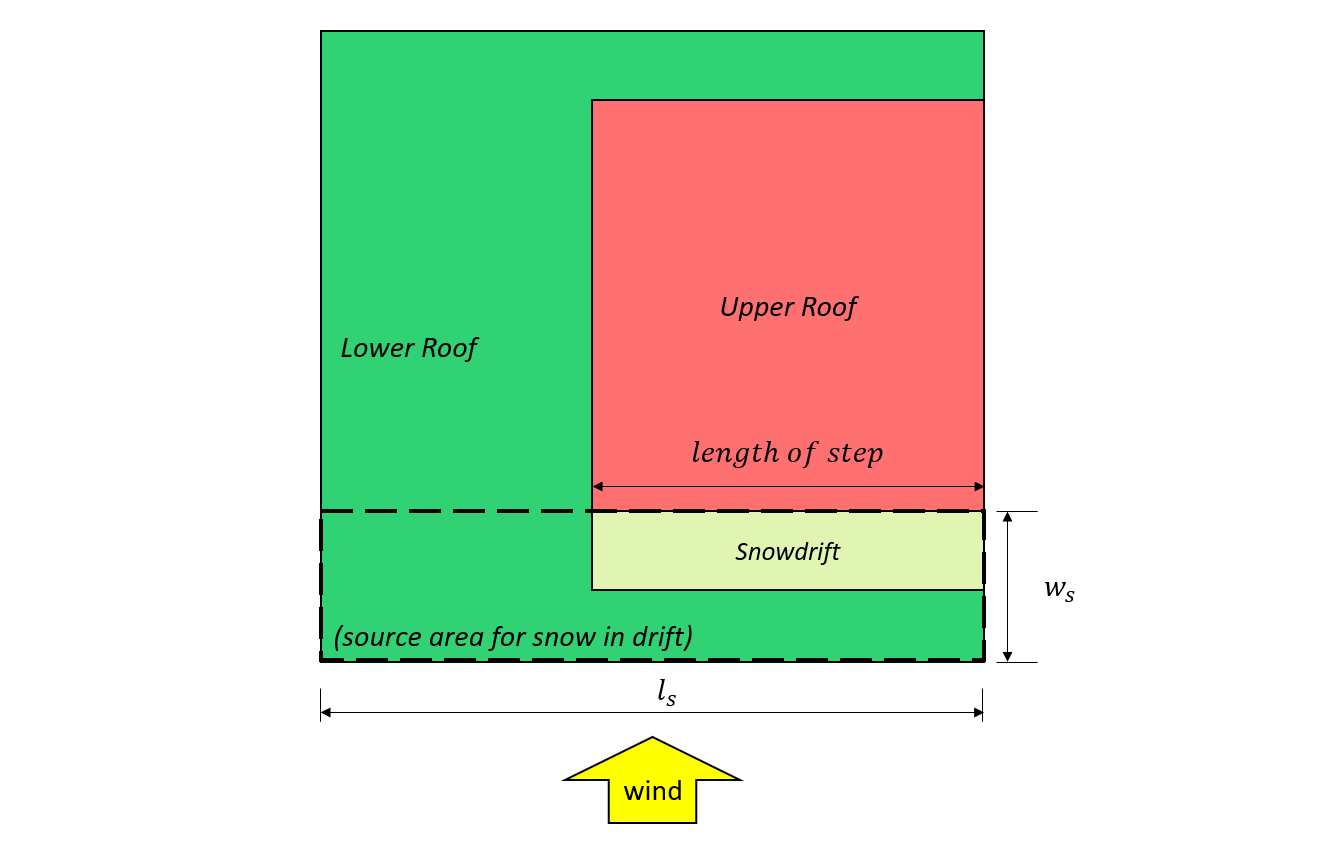
図 8: ケースⅡ – に基づいて、下部の屋根から来る風によって形成された雪の吹きだまり 図 4.1.6.5-B.

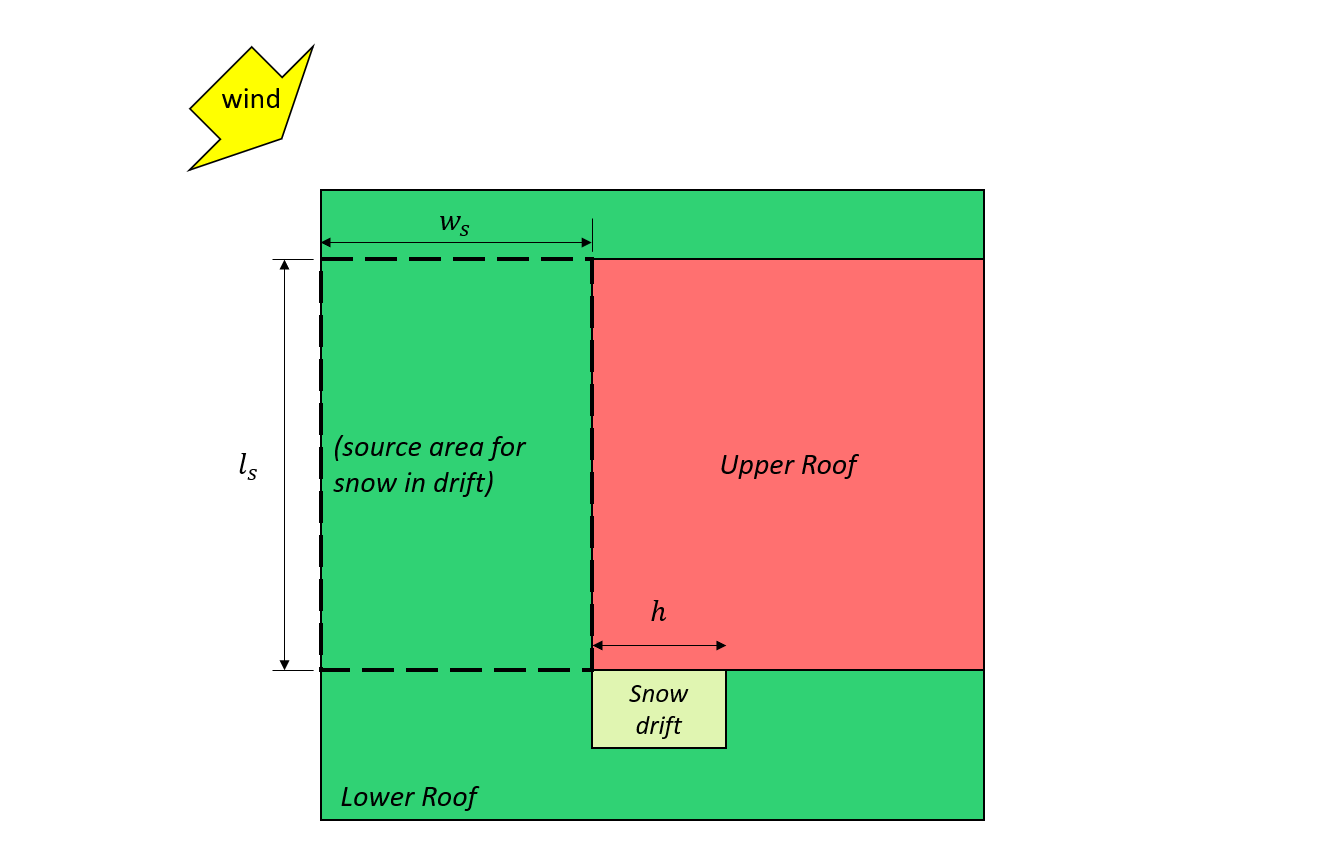
図 7: ケースⅢ – に基づいて、下部の屋根から来る風によって形成された部分的な雪の吹きだまり 図 4.1.6.5-B.

この例では, ケース I と II が考慮されます。.

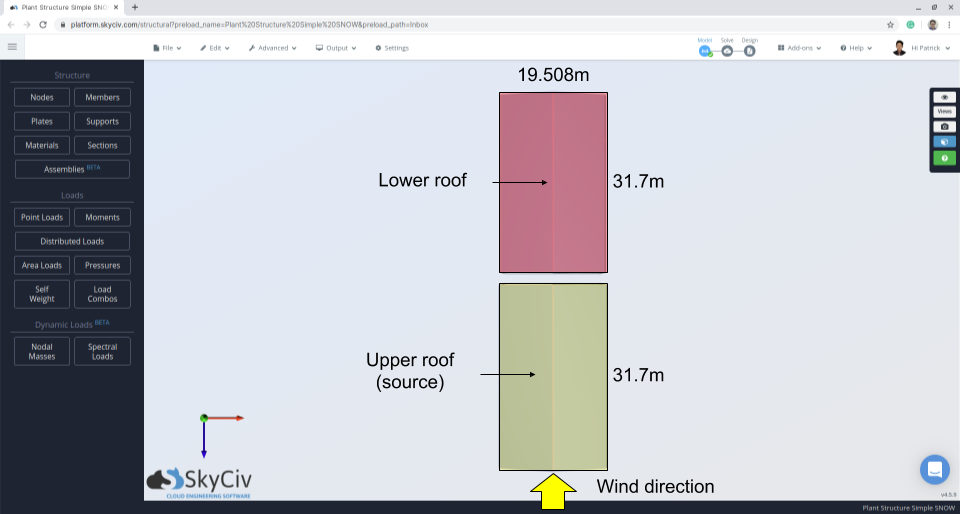
図 10: 風向と震源域を示す構造図.

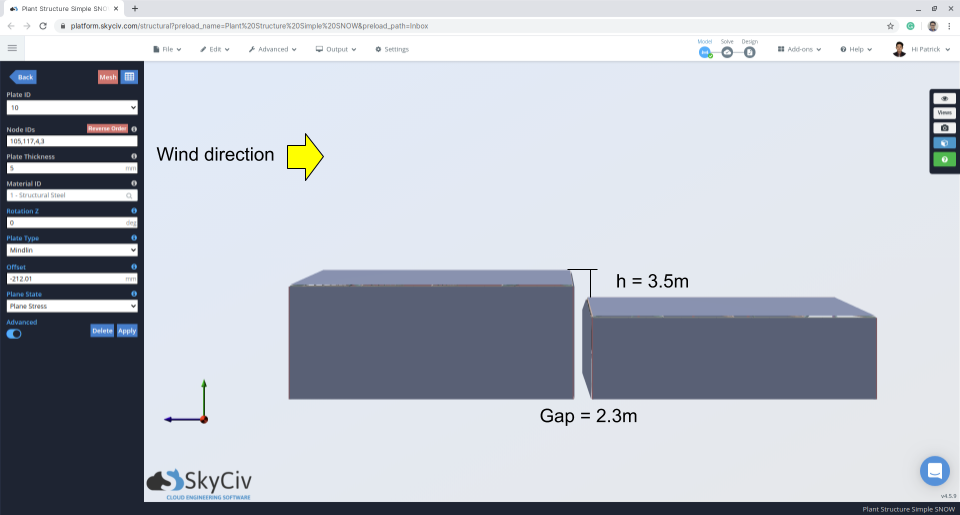
図 11: 上下の屋根の隙間と違いを示す立面図.

リッジに平行なアンバランス・ドリフトの場合, \({C}_{a}\) に基づいて、ケース I およびケース II について計算されます。 4.1.6.5 マルチレベル屋根の場合. ケースⅠの場合, これらの次のパラメータは、この例で前述したさまざまな式を使用して最初に計算する必要があります。:

\(β = 1.0\)
\({h}^{」} = (3.5) – \フラク{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m)
\({h}_{p} = 0\)
\({{h}_{p}}^{」} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m)
\(F = 0.35(1.0)\平方根{\フラク{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)

\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) または \({C}_{a0} = frac{3.66}{0.8} = 4.544\)
\({C}_{a0} = 4.544\)
\({バツ}_{d} = 5 \フラク{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 m)

これらのパラメータから, 累積係数, \({C}_{a}\), の値を代入することで計算できます。 \({C}_{a0}\) それぞれで \(バツ) 距離. 計算する必要があることに注意してください \({C}_{a}\) で \(x = a\) どこ \(a\) は屋根の隙間が小さいので、屋根の間の隙間です 5 で指定されたm 4.1.6.6.

で \(x = 0\): \({C}_{a} =4.544 – (4.544 – 1)(0/5.835) = 4.544\)
で \(x = a\): \({C}_{a} =4.544 – (4.544 – 1)(2.3/5.835) = 3.147\)
で \(x = {バツ}_{d}\): \({C}_{a} =1.0\)
で \(x = 10{h}^{」}\): \({C}_{a} =1.0\)

l l l , \({C}_{s} = 1.0\). しかも, 上屋根の規定積雪荷重を求める場合, 累積係数, \({C}_{a}\), と勾配係数, \({C}_{s}\), どちらも等しい 1.0. したがって, 各場所で指定された積雪荷重の大きさは:

で \(x = 0\): \(S=0.8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa\)
で \(x = a\): \(S=0.8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
で \(x = {バツ}_{d}\): \(S=0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
上部の屋根レベルで: \(S=0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)

尾根に平行な風の作用 – ケースⅡ – 下から上への風

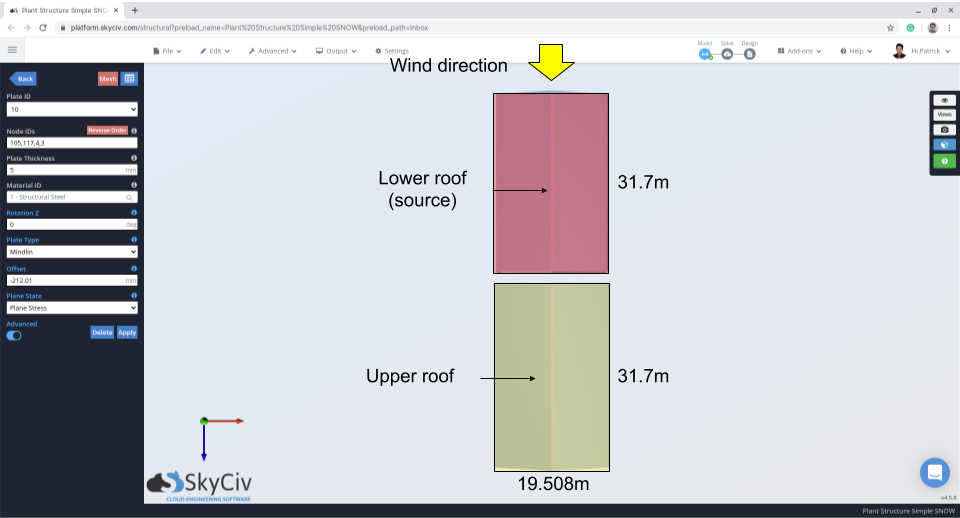
図 12: 風向と震源域を示す構造図 – 下の屋根から上の屋根への風.

ケースⅡの場合, 計算はケース I と似ていますが、 \(β = 0.67\):

\(β = 0.67\)
\({h}^{」} = (3.5) – \フラク{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m)
\({h}_{p} = 0\)
\({{h}_{p}}^{」} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m)
\(F = 0.35(0.67)\平方根{\フラク{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)

\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) または \({C}_{a0} = frac{2.70}{0.8} = 3.375\)
\({C}_{a0} = 3.375\)
\({バツ}_{d} = 5 \フラク{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 m)

で \(x = 0\): \({C}_{a} =3.375 – (3.375 – 1)(0/3.909) = 3.375\)
で \(x = a\): \({C}_{a} =3.375 – (3.375 – 1)(2.3/3.909) = 1.978\)
で \(x = {バツ}_{d}\): \({C}_{a} =1.0\)
で \(x = 10{h}^{」}\): \({C}_{a} =1.0\)

で \(x = 0\): \(S=0.8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa\)
で \(x = a\): \(S=0.8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
で \(x = {バツ}_{d}\): \(S=0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
上部の屋根レベルで: \(S=0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)

説明用, 対応します \({p}_{1}\), \({p}_{2}\), そして \({p}_{3}\) 図に示されています 13 そして 14 以下、ケース I および II の両方について, それぞれ.

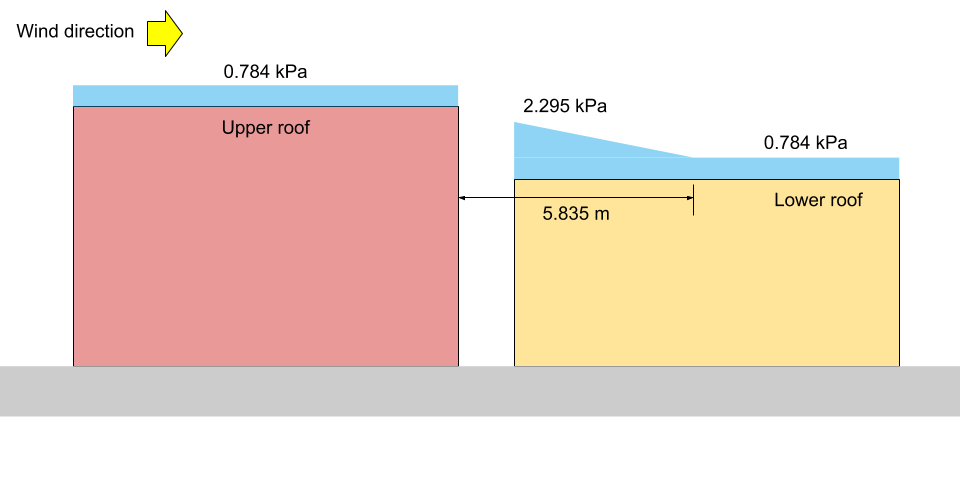
図 13: Case I の積雪荷重図 (スケールしない).

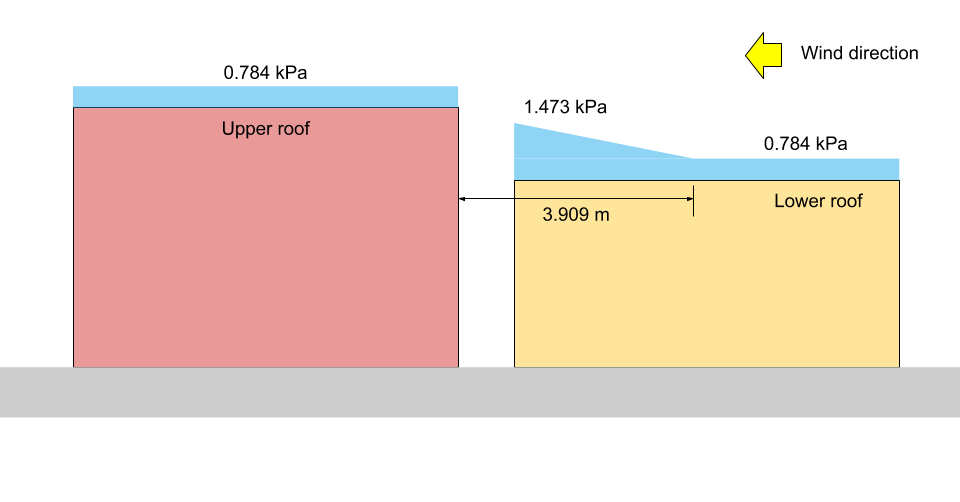
図 14: Case II の積雪荷重図 (スケールしない).

これらの計算を数分で自動的に完了します

長い計算だった, 将来のプロジェクトでこのプロセスをスピードアップするために、エンジニアとして何ができるか? 最近、SkyCiv は SkyCiv Load Generator の一部として Snow Load Generator をリリースして自動化しました, 風荷重も生成できます. 表示例の積雪荷重を求めるには, ツールを使用して数回クリックするだけです:

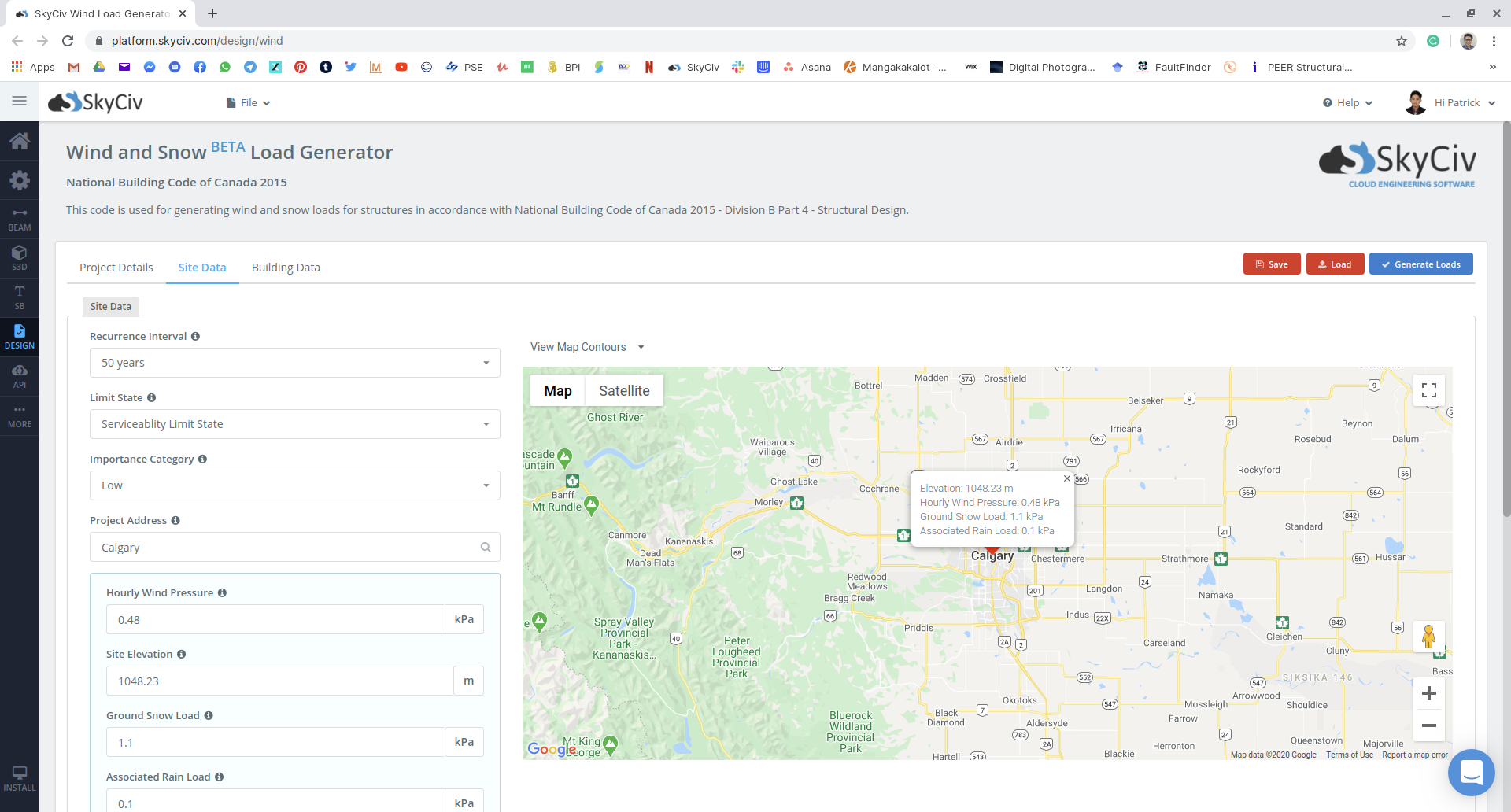
図 15: 私たちの例を使用した SkyCiv Load Generator モジュールへのサイト データ入力.

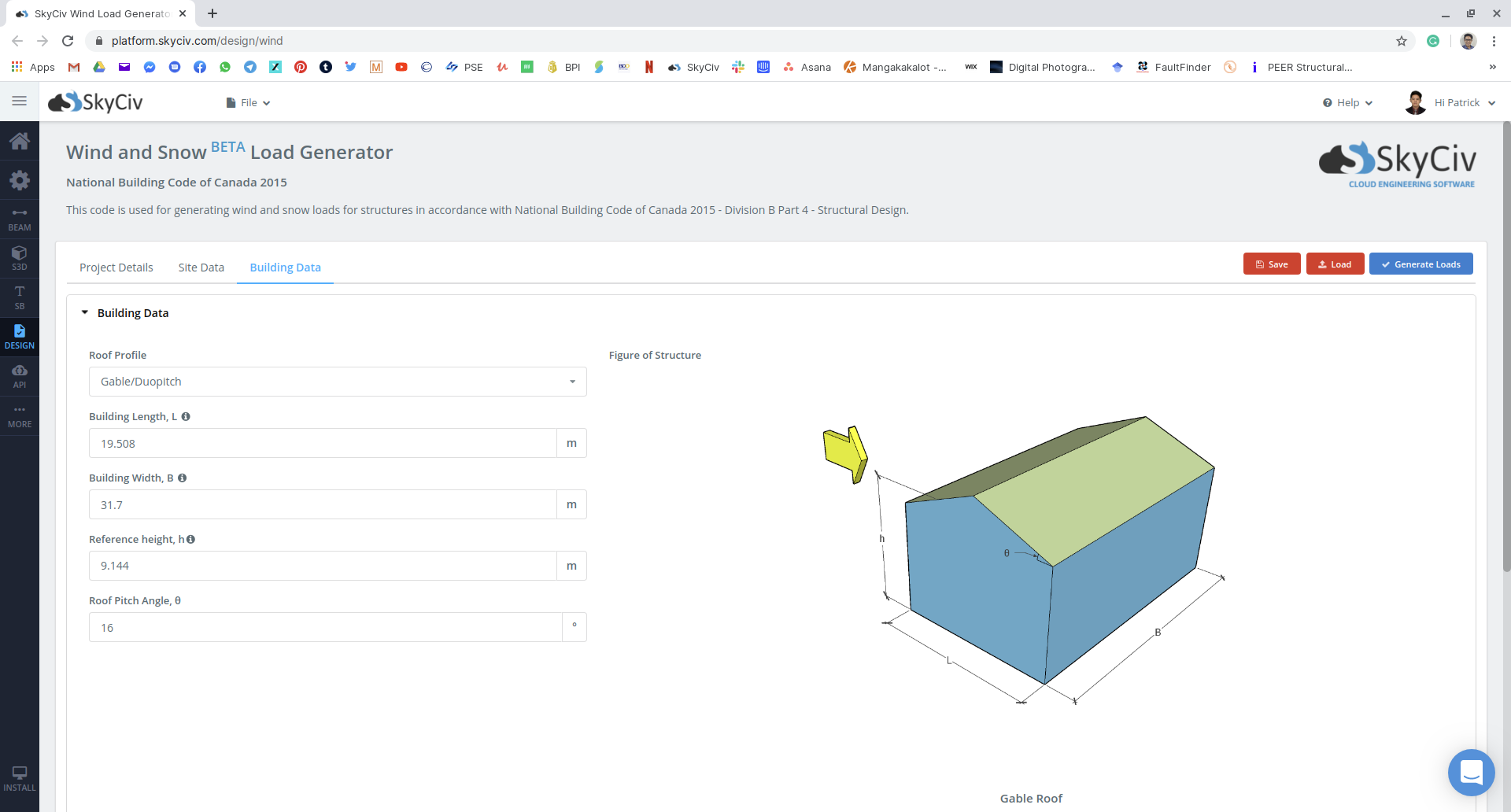
図 16: 私たちの例を使用したSkyCiv Load Generatorモジュールの建物と雪のパラメータ入力.

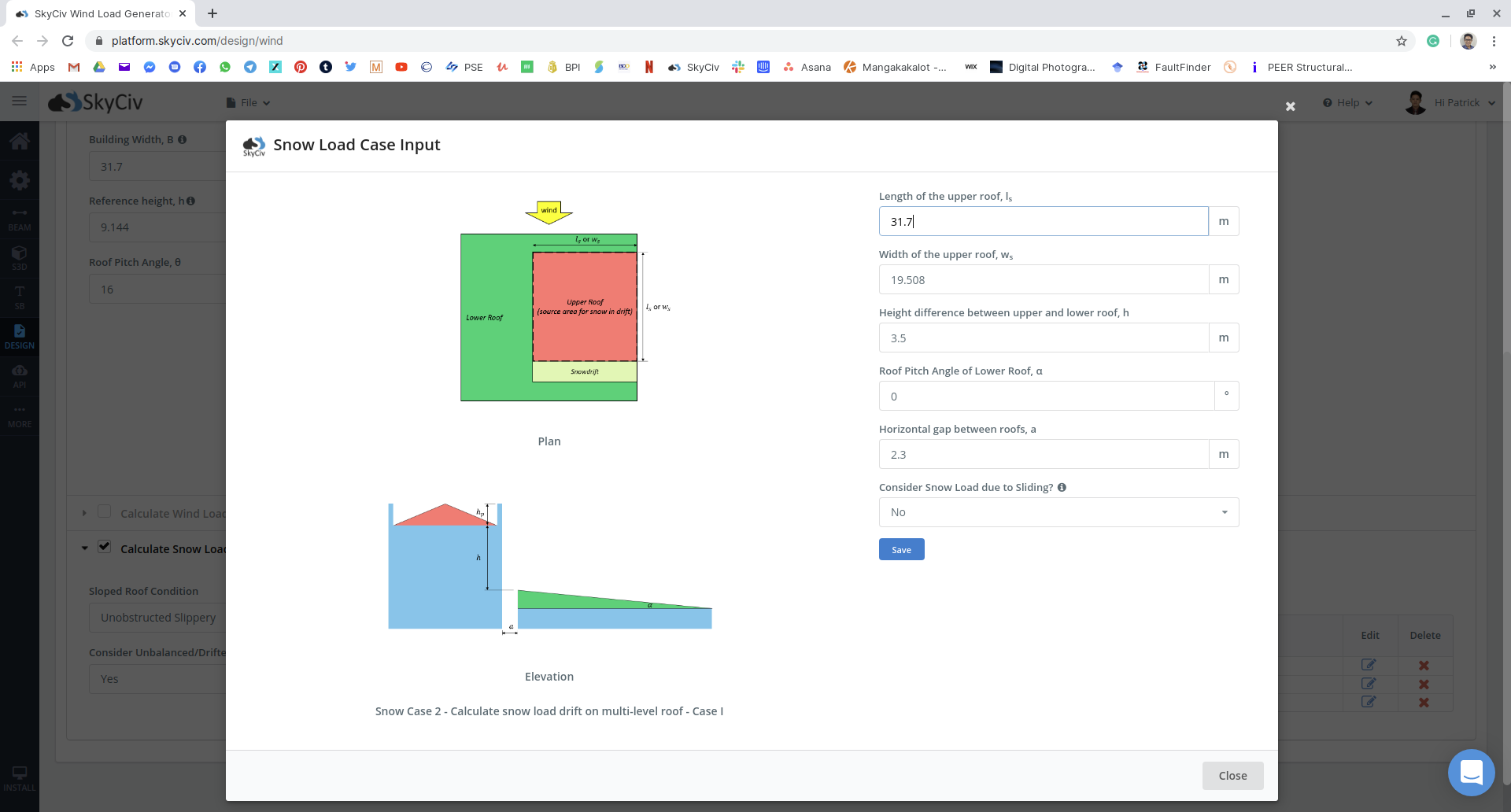
図 17: 例の複数のアンバランスな場合の積雪荷重入力.

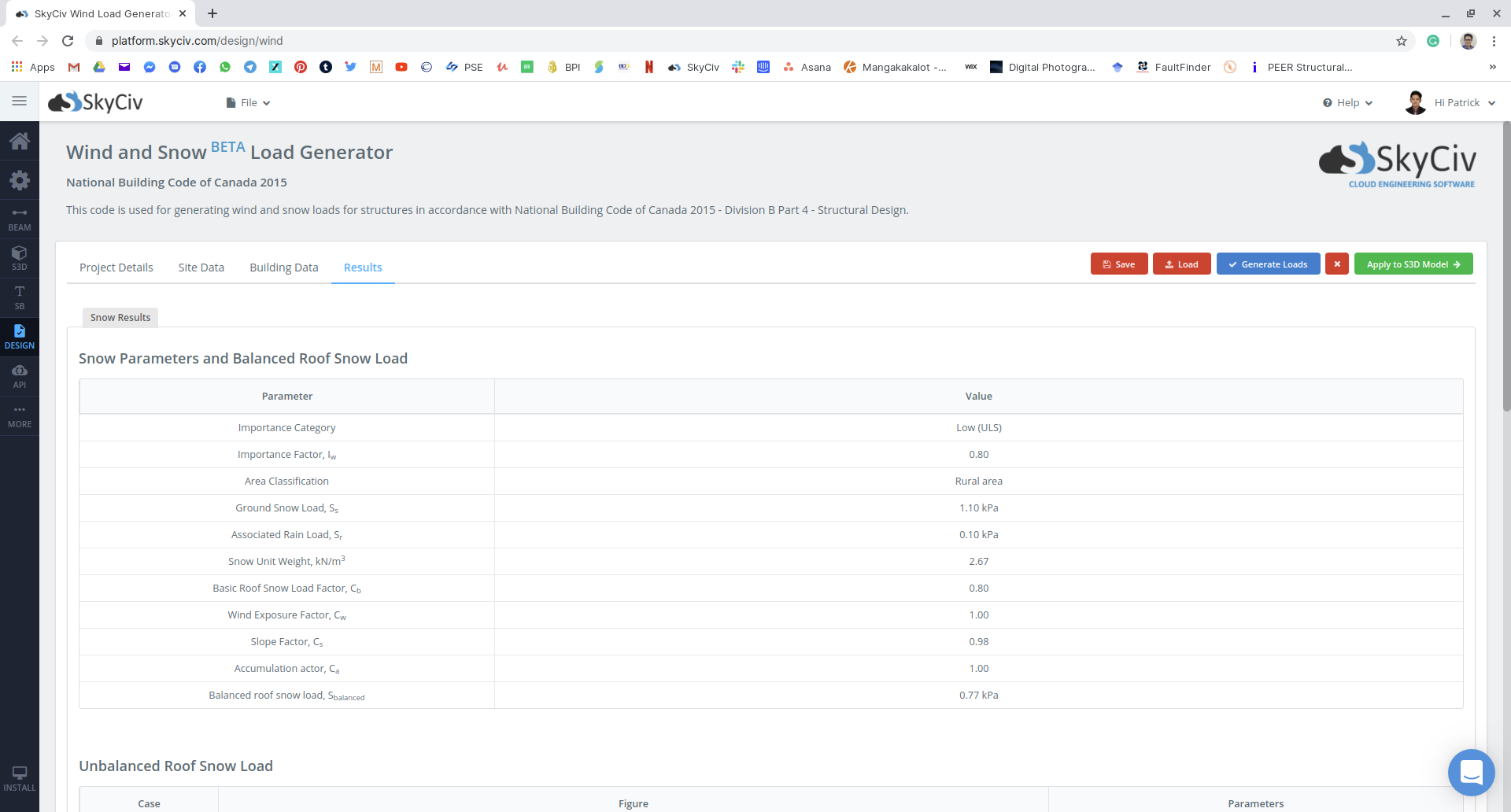
図 18: 使用された積雪荷重パラメータと構造に適用される平衡雪荷重のまとめ.

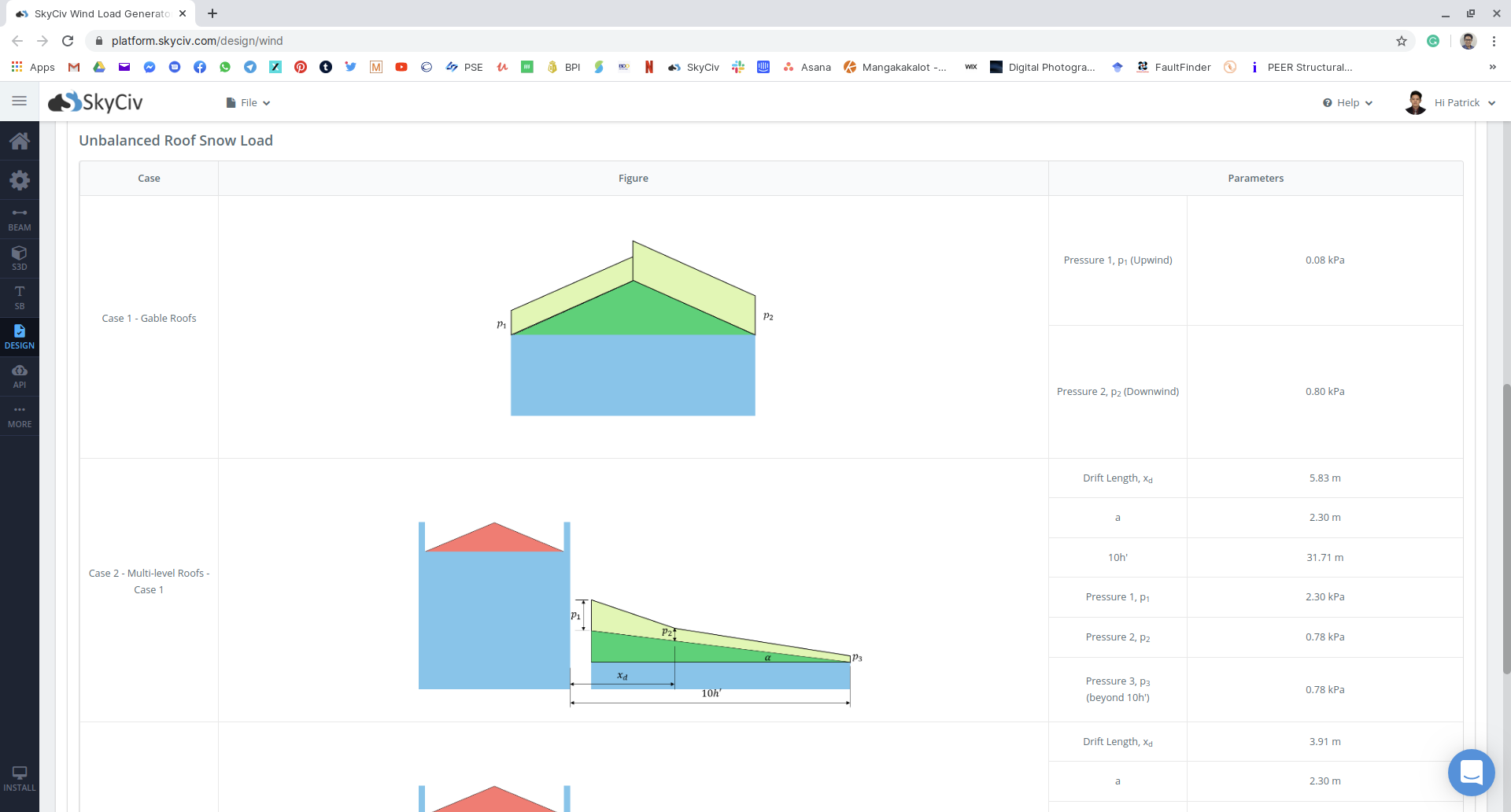
図 19: アンバランス積雪荷重結果のまとめ.

SkyCiv Load Generator モジュールの積雪負荷計算は、ASCE などの参照コードによってサポートされています 7-10, 7-16, に 1991-1-3, NBCC 2015, およびAS/NZS 1170.3, で入手できます スタンドアロン (負荷ジェネレータのみ) そして プロフェッショナル アカウント. プログラミングと API に精通している? この機能は、 SkyCiv API.

SkyCiv雪負荷計算機

参考文献:

• カナダ国立研究評議会. (2015). カナダの建築基準法, 2015. カナダ国立研究評議会.

注意:

• の NBCC コード リファレンス “基本的な屋根雪負荷係数” — 探す 4.1.6.2 文 (2)
• の NBCC コード リファレンス “風露出係数” — 探す 4.1.6.2 文 (3) そして (4)
• の NBCC コード リファレンス “勾配係数” — 探す 4.1.6.2 文 (5), (6), そして (7)
• の NBCC コード リファレンス “累積係数” — 探す 4.1.6.2 文 (8), 4.1.6.5 マルチレベル屋根用, 4.1.6.6 隙間のある屋根用, そして 4.1.6.9 切妻屋根用