SkyCiv Structural 3Dで構造をモデリングするとき, メンバーと接続は、メンバーのノードとラインで簡素化されます. ノード間のこれらの線は、単純さと連続性のために、常に各メンバーの重心を通過します. 実際には, メンバーに作用する荷重がその重心によって正当化できない場合に状況が発生します, これは偏心荷重です. エンジニアは、部材を設計するときに偏心荷重について考える必要があります。, または ねじれ, できる, そしておそらくそうなるでしょう, 断面の限界状態に影響を与える.
例えば: 片持ち床の上からの点荷重, または補強材に取り付けられた梁の側面からぶら下がっている荷重. 偏心荷重とその解釈方法の簡単な図を図に示します。 1.
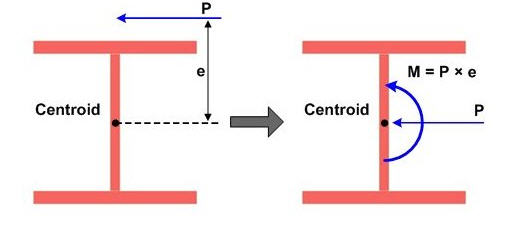
図 1: I字断面への偏心荷重の例
ソース: http://manual.midasuser.com
SkyCiv Structural 3Dの例を見て、偏心点荷重を2つの異なる方法で適用しましょう. 最初, W14x22 ビームがあると仮定しましょう。 15 フィートの長さで、スパンの中央に偏心点荷重があります 10 キップ, 演技 12 重心から数インチ. 負荷が下向きに作用していると仮定します (-Y方向) そして左側へ (+Z 方向) メンバーの. また, 自重がオフであると仮定します, 簡単にするために.
単一のメンバーをモデル化する場合, 偏心荷重をモデル化するときは、サポートが正しいことを確認してください. 梁の両方のサポートが 3D ピンとして設定されている場合、解析は実行されません。これは、どちらのサポートも断面の回転に抵抗しないためです。. 私たちの場合には, 原点から離れたサポートは、X および Y 方向の回転を可能にする 2D ピンのみです。, 垂直方向と水平方向のたわみから来る. 3D モデリング スペースでメンバーの例を見てみましょう:
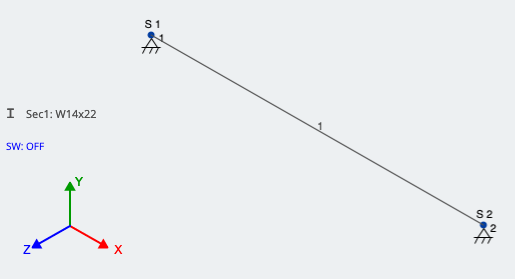
今, 負荷の偏心を説明する 2 つの方法を見てみましょう. 図を参照 1, 私たちの場合には:
\({P} = {10} キップ)
\({e} = 12 インチ = 1 足)
方法 1: モーメントを適用して風変わりさを考慮する
図に示すように 1, 部材の重心に追加のモーメントを適用することで、荷重の偏心を考慮することができます. このモーメントは、点荷重にモーメント アームを乗じて得られます。, または “e”. ポイントロード自体を考慮する必要があります, だからあるでしょう (2) 特定された場所での荷重.
私たちの場合には:
\({M} = {P}*{e}\)
\({M} = 10 キップ * 1 足 = 10 kip-ft)
述べたように, このモーメントは、部材に沿った偏心点荷重と同じ位置に適用されます。. SkyCivは、適用されている軸を中心に反時計回りとして正のモーメントを認識します, 私たちの場合、グローバルX軸の周りです. 図を参照 3 SkyCiv 3Dで適用されるこれらの負荷の:
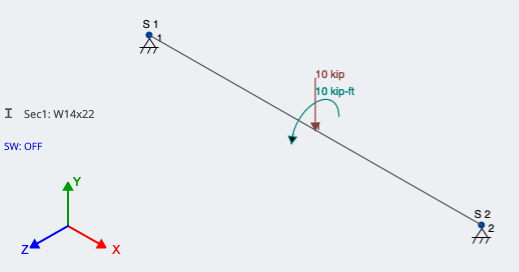
図 3: 追加のモーメントを適用することによる偏心荷重のモデル化
方法 2: リジッド リンクの使用
別の方法は、固定リンクを使用することです. リジッドリンク 接続されているものに合わせて回転および移動する架空のメンバーと見なされます. ノード間でたわみがなく、完全に固い. リジッド リンクは、3D モデリング スペースでライト グレーとして識別され、 “R” 彼らの隣に, 図に示すように 4. それらは要素と負荷を接続するためにより多く使用されるため, サイズまたはセクション ID が必要です.
私たちの例では, ノード 6 メンバーのミッドスパンにあります. ノード 5 同じX座標にあります, だが 1.0 +Z 方向のフィート; ノード 5 偏心荷重の実際の位置.
2 つのノード間のメンバーを作成/描画する, それをリジッド リンクとして割り当てます. これを行うには、 高度な メンバーウィンドウで切り替える, その後に行きます タイプ そしてそれをに変更する リジッドリンク. 適用後, メンバーは上記のように見えるはずです. 一方の端は偏心荷重の実際の位置を示し、もう一方の端は部材に垂直方向に接続されています, 負荷は最終的に適用できます. これを図に示します 4; 赤い矢印はリジッド リンクを指しています:
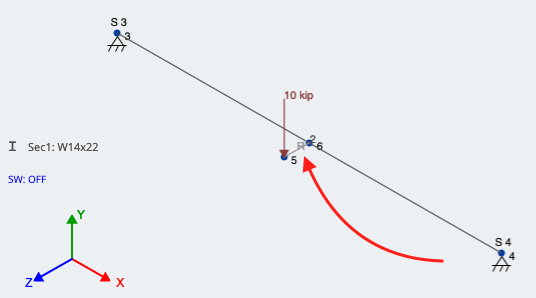
図 4: 剛体リンクを使用して点荷重の偏心を考慮する
最終的な比較と分析:
線形静解析を実行して結果を見てみましょう. 下向きの力が見られるはずです 10 荷重位置でのねじれ成分に加えてキップ. 両方
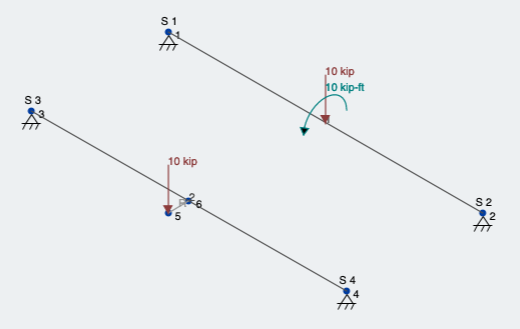
図 5: 偏心荷重の両荷重条件
最初, 反応とモーメントの結果を見てみましょう (図 6):
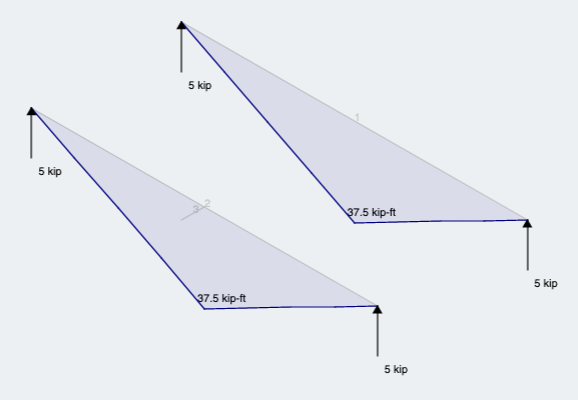
図 6: 両方の方法の反力とモーメントの結果
予想通り、同じ大きさの荷重と部材に沿った位置から予想されることがわかります, しかし重心を通して.
その後, 偏心のせいで, 両方のメンバーが同じ結果を出し、メンバーが また ねじれを経験する (図 7):
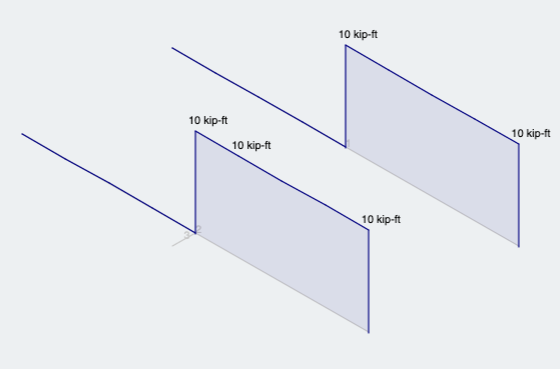
図 7: 両方の方法のねじり解析結果
構造エンジニア
ベン (民事)


