不確定なビームを計算する方法 – 二重積分法

不定 ビーム 反応を解決するために必要な追加の手順のため、課題になる可能性があります. 不確定な構造には、いわゆる不確定性があることを忘れないでください. 構造を解くには, 境界条件を導入する必要があります. したがって, 不確定性の程度が高いほど, より多くの境界条件を特定する必要があります. しかし、不確定なビームを解決する前に, 最初に、ビームが静的に不確定であるかどうかを識別する必要があります. 梁は一次元構造なので, 式を使用して外部的に静的に不確定な構造を決定するだけで十分です.

[数学]
私_{e}= R- left ( 3+e_{c} \正しい )
[数学]

どこ:

• 私_e =不確定性の程度
• R =反応の総数
• e_c =外部条件 (例えば. 内部ヒンジ)

通常, しかしながら, 不確定性の程度を解く必要なし, 単純なスパンまたは片持ち梁以外のものは静的に不確定です, そのようなビームには内部ヒンジが付属していないと仮定します.

不定ビームを解決するには、多くのアプローチ方法があります. シンプルさとSkyCivビームとの類似性のために 手計算, 二重積分法について説明します.

二重積分

二重積分は、おそらくビームの分析のためのすべての方法の中で最も簡単です. この方法の概念は、主に積分計算の基本的な理解に依存しているため、他の方法とは対照的に非常に簡単です。, したがって、名前. ビームの曲率とモーメントの関係から、微積分が少し調整されます。これを以下に示します。.

[数学]
\フラク{1}{\rho}= frac{M}{番号}
[数学]

1 /ρはビームの曲率であり、ρは曲線の半径であることに注意してください。. 基本的に, 曲率の​​定義は、弧長に対する接線の変化率です。. モーメントは部材の長さに対する荷重の関数であるため, 部材の長さに関して曲率を積分すると、梁の勾配が得られます. 同様に, 部材の長さに対して勾配を積分すると、ビームのたわみが生じます. 典型的な構造荷重は本質的に代数的であるため, これらの式の積分は、一般的な電力式を使用するのと同じくらい簡単です。.

[数学]
\int f left ( x右 )^{ん}dx = frac{f left ( x右 )^{n + 1}}{n + 1}+C
[数学]

おそらく、概念を理解するための最良の方法は、次のようなビームの例を提供することです。.

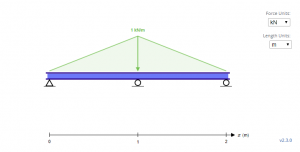
上記のサンプルビームは、三角形の荷重を伴う不確定なビームです. とともに サポート, あ_そして, B_そして およびC_そして 最初に, 2番目, それぞれと3番目のサポート, これらの未知数を解くための最初のステップは、平衡方程式から始めることです。.

ビームの次数があることに注意してください。 静的不確定性 1°の. 4つの未知数があるので (あ_バツ, あ_そして, B_そして, およびC_そして) 上記の平衡方程式からこれまでのところ3つの方程式があります, 境界条件からもう1つの方程式を作成する必要があります. 点荷重と三角形荷重によって生成されるモーメントは次のとおりであることを思い出してください。.

点荷重:

[数学]
M = F times x; M = Fx
[数学]

三角荷重:

[数学]
M = frac{w_{0}\x倍}{2}\倍左 ( \フラク{バツ}{3} \正しい ); M = frac{w_{0}x ^{2}}{6}
[数学]

二重積分法を使用することにより, これらの新しい方程式が作成され、以下に表示されます.

注意: 上記の方程式は、式がゼロに等しいマコーレー関数として記述されています。 バツ < L. この場合, L = 1.

上記の方程式では, 追加された第4項がどこからともなく出てきているように見えることに注意してください. 実際には, 荷重の方向は重力の方向と反対です. これは、三角形の荷重の方程式が機能するのは、長さが長くなるにつれて荷重が上昇している場合のみであるためです。. これは、次の方程式ではあまり問題になりません。 分散 そして 点荷重 それらの対称性のために. 実際に, 上のビームの同等の荷重は、下のビームのように見えます, したがって、方程式はそれに基づいています.

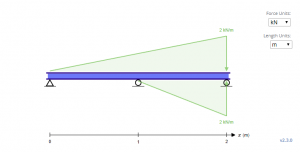
Cを解くには₁ およびC₂, 境界条件を決定する必要があります. 上のビームで, このような境界条件が3つ存在することがわかります。 バツ = 0, バツ = 1, そして バツ = 2, ここで、たわみyは3つの場所でゼロです。.

境界条件 1

[数学]
x = 0, y = 0; C_{2}=0
[数学]

境界条件 2

[数学]
x = 0, y = 0; C_{1}= frac{1}{120}-\フラク{A_{そして}}{6}
[数学]

各定数の値を決定した後, 最後の方程式は、最後の境界条件を使用して取得できるようになりました。.

境界条件 3

θ=の境界条件に注意してください。 0 x = 1 に使える, ただし、対称荷重のある対称連続梁の中間反力にのみ適用できます。.

4つの方程式が決定されたので, それらは同時に解決できるようになりました. これらの方程式を解くと、次の反応が得られます.

決定された反応で, 反応の値は、モーメント方程式に代入して戻すことができます. これにより、ビームシステムの任意の部分のモーメントの値を決定できます。.

二重積分のもう1つの便利な点は、モーメント方程式が、以下に示す関係でせん断を解くために使用できる方法で提示されることです。.

[数学]
V = frac{dM}{dx}
[数学]

再び, 微分学の基本的な理解のみを使用する, 関数の導関数をゼロに等しくすると、その関数の最大値または最小値が得られます。. したがって, V =を等しくする 0 で最大の正のモーメントになります バツ = 0.447 そして バツ = 1.553 Mの= 0.030

もちろん, これはすべてSkyCivBeamで確認できます.

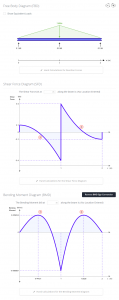
SkyCiv Beamソフトウェア

SkyCiv ビーム解析ソフトウェア ユーザーはビーム構造を簡単かつ正確に解析できます. 梁メンバーの分析を取得できます, 含む 反応, 剪断力, 曲げモーメント, 偏向, そして ストレス ほんの数秒で.

まずはやってみたい方は, 無料ビーム電卓 始めるのに最適な方法です, または、今すぐ無料でサインアップしてください!