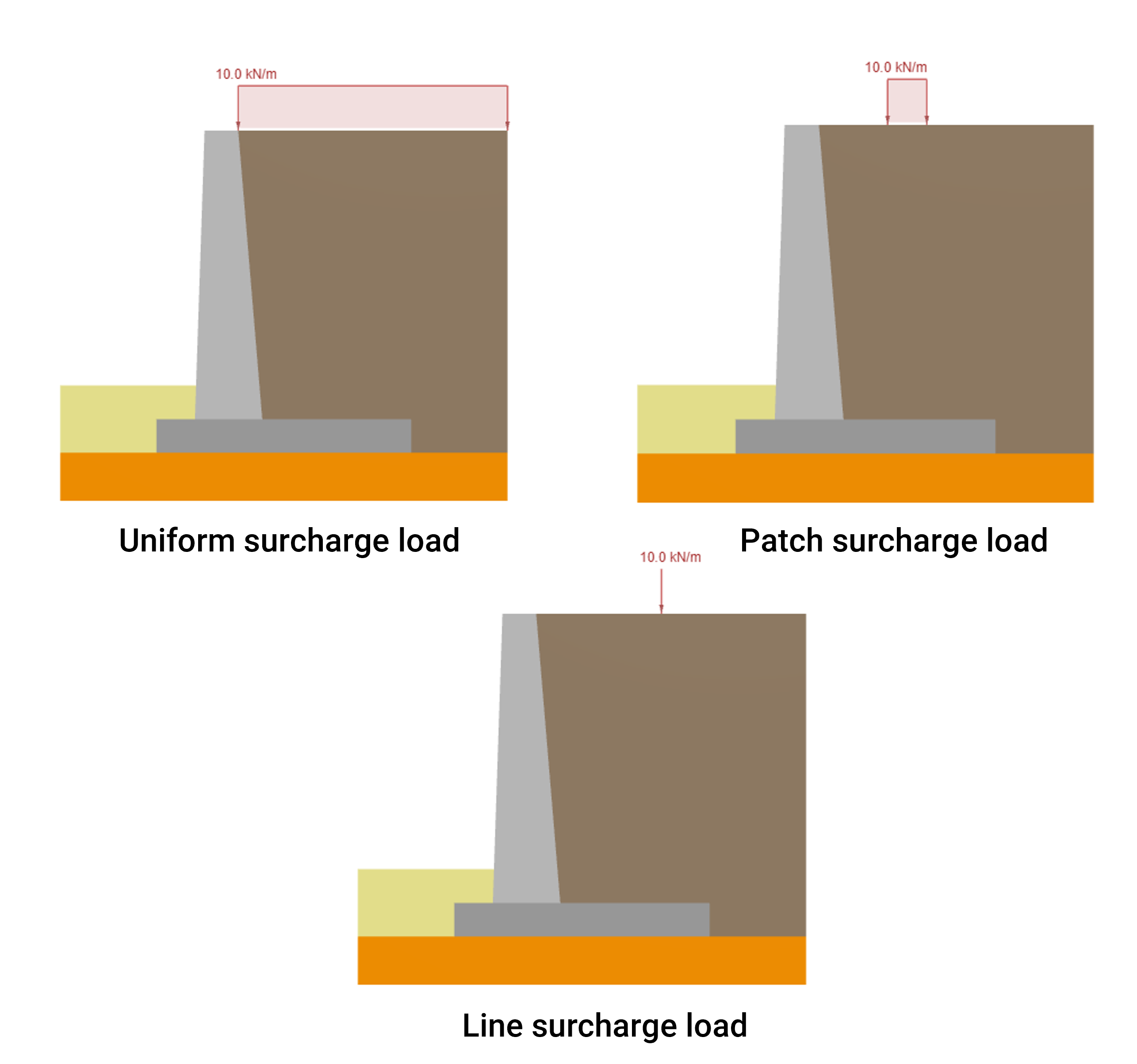
擁壁上載荷重による横土圧の計算
追加荷重による側方土圧の計算擁壁の両側の土壌ゾーンには、通常、いくつかの追加の外部荷重が適用されます. それらは、車両の通行などの擁壁のライブ追加負荷である可能性があります, 歩行者交通, と駐車場, または斜面侵食に対する保護システムなどの永久負荷, および隣接する構造物. 記事上で, 3 種類の重荷重または追加荷重によって擁壁の背面に作用する横方向の土圧を計算する方法に焦点を当てます。:
- 追加荷重による側方土圧の計算 3種類の重ね荷重により擁壁の背面に作用する側方土圧の計算方法に焦点を当てます。
- 3種類の重ね荷重により擁壁の背面に作用する側方土圧の計算方法に焦点を当てます。 3種類の重ね荷重により擁壁の背面に作用する側方土圧の計算方法に焦点を当てます。
- 3種類の重ね荷重により擁壁の背面に作用する側方土圧の計算方法に焦点を当てます。 3種類の重ね荷重により擁壁の背面に作用する側方土圧の計算方法に焦点を当てます。
追加荷重による側方土圧の計算擁壁の両側の土壌ゾーンには、通常、いくつかの追加の外部荷重が適用されます
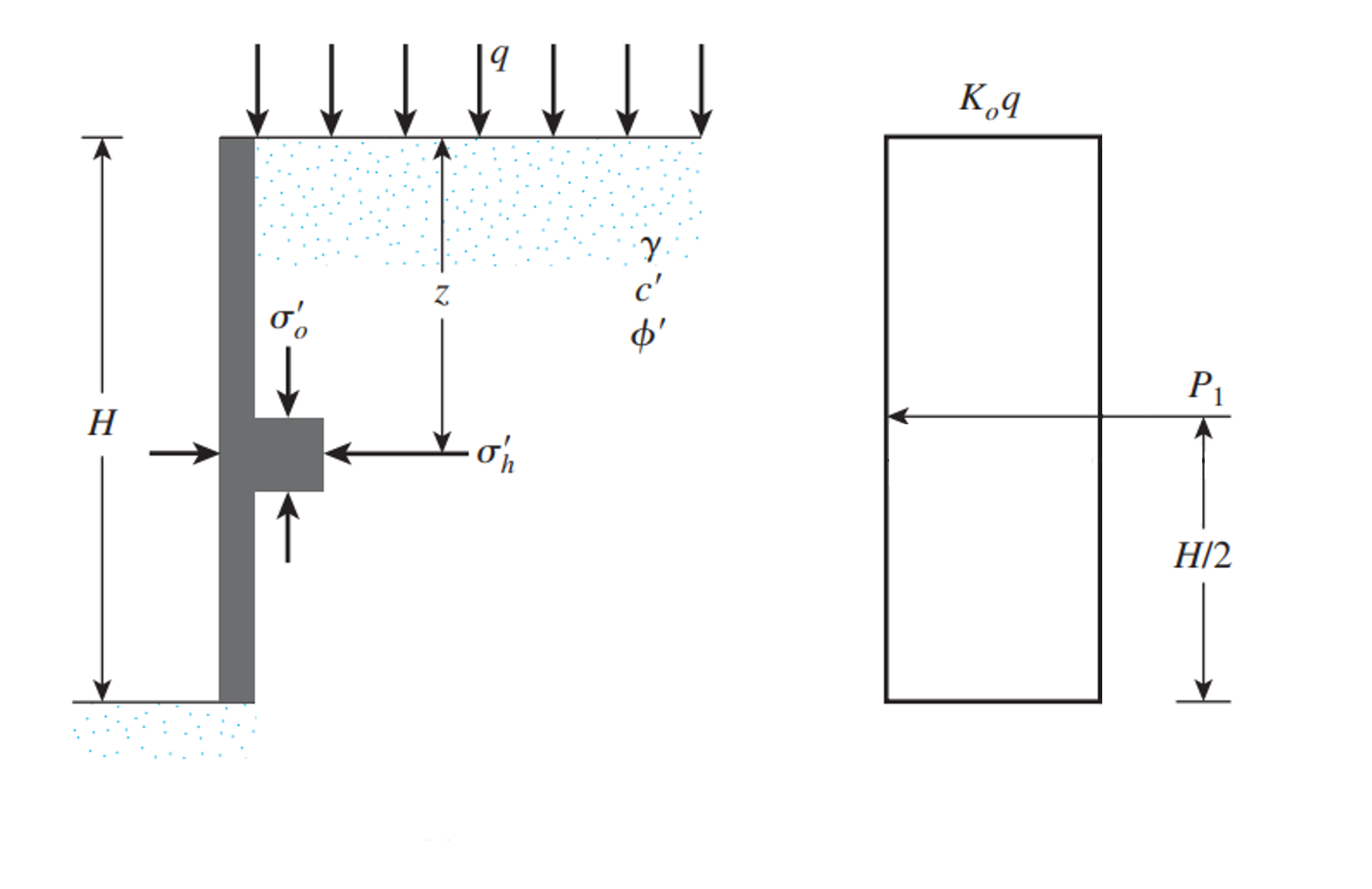
擁壁に適用される永久または活荷重が均一であり、無限分布荷重であると仮定できる場合, 追加荷重による側方土圧の計算擁壁の両側の土壌ゾーンには、通常、いくつかの追加の外部荷重が適用されます. そんな理由で, 合力の位置は、壁の全高の中央です。. 傾斜裏込めの場合, 圧力分布は、バックフィルの傾斜に等しい角度で歪んでいます. この場合, 結果の計算は次のようになります:
- 静止状態の土壌の場合:
\(P_{dist, \; 安静時に} = K_{0} \cdot q cdot H_{土}\)
- cdot q cdot H_soil :
\(P_{dist, \; 下部構造土} = K_{a} \cdot q cdot H_{土}\)
- cdot q cdot H_soil :
\(P_{dist, \; 受け身} = K_{p} \cdot q cdot H_{土}\)
前に述べたように, 分布が一様だから, 結果の位置は、土壌の高さの真ん中にあります.
から適応: それか, B. M. (2010). 基礎工学の原則, SI版. 章 7 横土圧. センゲージ ラーニング. 図 7.3
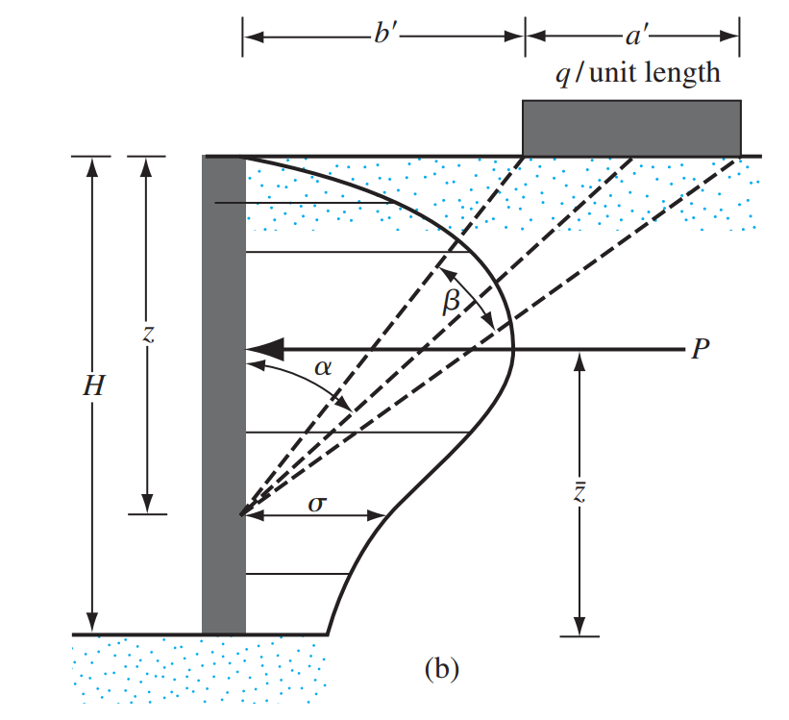
パッチロード
擁壁のパッチまたはストリップ追加料金の場合, 単位長さあたりの総力は、次のように表すことができます。:
\(P_{パッチ} = frac{q}{90} [H(\theta_2-theta_1)]\)
どこ,
\(\theta_1 = tan^{-1}(\フラク{b’}{H}) (君は)\)
\(\theta_2 = 日焼け^{-1}(\フラク{a’ + b’}{H}) (君は)\)
パッチまたはストリップ荷重による横土圧からのこの合力は、次の場所にあります。 \(\バー{と}\) 圧力分布の下から測定, \(\バー{と}\) 次の式を使用して推定できます:
\(\バー{と} = H – [\フラク{H^2(\theta_2-theta_1) + (R-Q) – 57.3a'H}{2H(\theta_2-theta_1)}]\)
どこ \(R = (a’+b’)^2cdot(90 – \theta_2)\) そして \(Q = b'^2(90-\theta_1)\)
から撮影: それか, B. M. (2010). 基礎工学の原則, SI版. 章 7 横土圧. センゲージ ラーニング. 図 7.14
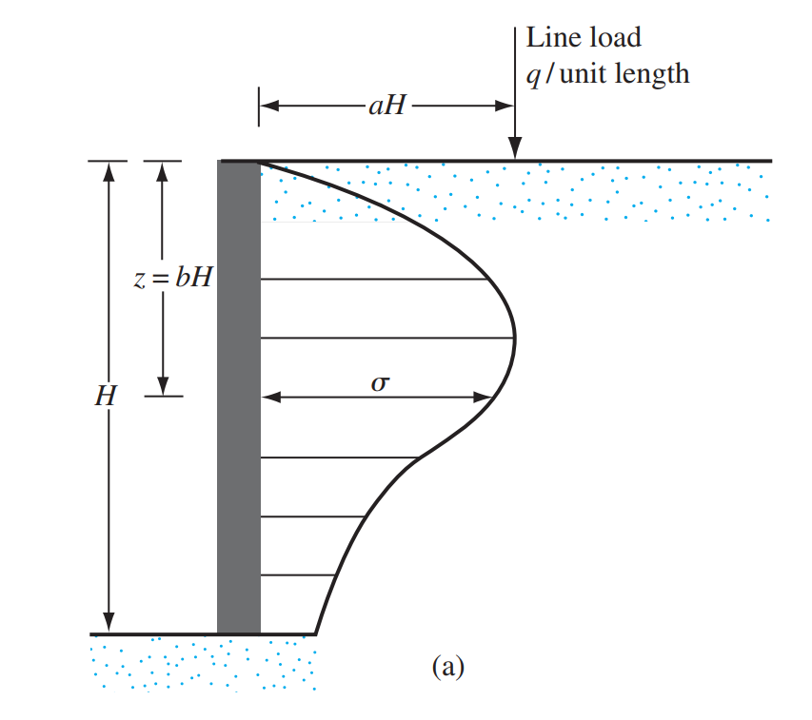
線負荷
最後に, 擁壁にライン追加料金がかかる場合, 任意の深さでの擁壁の背面にかかる応力 \(z), 次のように表現できます。:
\(\シグマ = frac{4q}{\フィートH} \フラク{a^2b}{(a^2 + b^2)^ 2}\) ために \(a > 0.4\)
\(\シグマ = frac{q}{H} \フラク{0.203 b}{(0.16+ b^2)^ 2}\) ために \(leq 0.4\)
から撮影: それか, B. M. (2010). 基礎工学の原則, SI版. 章 7 横土圧. センゲージ ラーニング. 図 7.14
から上記の式を統合する \(b = 0\) に \(b = 1\), 加えられた線荷重の応力分布による合力の値を取得することが可能です:
\(P_{ライン} = int_{0}^{H}\シグマ ,dz = – \フラク{4 H^2a^{2} q}{2 H^2a^{2} \パイ + 2 H^2 pi} + \フラク{2 q}{\パイ} = frac{2 q}{\円周率 左(^{2} + 1\正しい)}\) ために \(a > 0.4\)
\(P_{ライン} = int_{0}^{H}\シグマ ,dz = 0.546875 q \) ために \(leq 0.4\)
合力の位置を計算するため, 任意の深さでの応力の初期式は、2 つの区間で積分されます, からの1つ \(b = 0\) に \(b = b_r) そしてもう一方から \(b = b_r) に \(b = 1\), その後, 両方の式は方程式に代入され、その解は横方向の圧力分布からの合力の位置です。:
\(\バー{と} = H 左(1 – sqrt{\フラク{1}{2 ^{2} + 1}}\正しい)\) ために \(a > 0.4\)
\(\バー{と} = H (1- 0.348155311911396) \) ために \(leq 0.4\)
結論
重畳荷重による横土圧合力とその位置を正確に推定することは、擁壁設計プロセスの重要なステップです。. この側方土圧が擁壁設計プロセスにどのように含まれているかについての詳細は、, 記事参照 ここに.
追加負荷による横方向の土圧とは別に, 土の自重も擁壁の背面に圧力をかけます, 静止時のようなさまざまな土壌条件でこの圧力を計算する方法の詳細, 下部構造土, およびパッシブについては別の記事で説明します ここに.
参考文献
擁壁計算機
SkyCivは、壁の側方土圧を計算する無料の擁壁計算機を提供します, 擁壁の安定性分析を実行します. の場合、ベースの下部から壁の高さの半分, の場合、ベースの下部から壁の高さの半分, 転倒に対する擁壁の安定性を計算する方法, スライディング, とベアリング!
製品開発者
ベン (民事)
