CSA A23.3-14 に基づく独立基礎設計の計算ガイド

SkyCiv Foundation は、CSA A23.3-14¹ および NBCC に準拠した独立基礎の設計をカバーしています。 2010².

SkyCivのFoundationDesignソフトウェアを試してみたい? 当社のツールを使用すると、ユーザーはダウンロードやインストールを行わなくてもFoundationDesignの計算を実行できます。!

基礎設計計算機

独立基礎の設計パラメータ

提示された計算の一部は ACI と類似しています 318, これは、CSA の対応する参考資料の 1 つでもあります。.

寸法要件

独立基礎の寸法を決定するには, サービスまたはファクタリングされていない負荷, 死んだなど (D), 住む (L), 風 (W), 地震 (E), などは、荷重の組み合わせを使用して適用されます, NBCC の定義による 2010. どちらの荷重の組み合わせが支配するかは、設計荷重と見なされます, 式に示すように、許容土圧に除算されます。 1.

\(\テキスト{あ} = frac{\テキスト{P}_{\テキスト{ん}}}{\テキスト{q}_{\テキスト{全て}}} \右矢印 \) 方程式 1

どこ:
q_全て =許容土圧
P_ん =ファクタリングされていない設計荷重
A =基礎エリア

一方向せん断

確認するには 一方向せん断, 臨界せん断面 (図を参照してください 1) 離れた場所にあります “d” 柱の表面から.

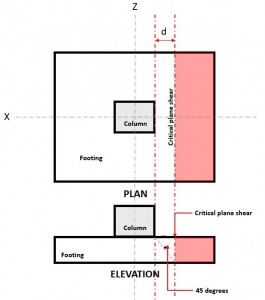
図 1. 一方向せん断の臨界面せん断

の 一方通行 剪断 要求する または V _f 基礎が、領域がある柱から片持ち梁で離れていると仮定して計算されます (赤) 図に示されている 2, に従って CSAA23.3-14, セクション 13.3.6.

の 一方向せん断耐力 または V _c は極限せん断強度として定義され、式を使用して計算されます 2 あたり CSAA23.3-14, セクション 11.3.4.

\(\テキスト{V }_{\テキスト{c}} = phi _{\テキスト{c}} \倍ラムダ倍平方根{\テキスト{f ’}_{\テキスト{c}}} \倍 text{b}_{\テキスト{w}} \倍 text{d} \右矢印 \) 方程式 2 (CSA A23.3-14 等式. 11-6)

どこ:
ϕ_c = コンクリートの抵抗係数
λ = コンクリート密度の修正係数
f’_c =指定されたコンクリート強度, MPa
b_w =基礎の幅, んん
d = 有効せん断深さ, んん

の設計要件を満たすために、せん断需要とせん断能力は次の式を満たす必要があります。 CSAA23.3-14:

\(\テキスト{V }_{\テキスト{f}} \leq phi text{V }_{\テキスト{c}} \右矢印 \) 方程式 3 (CSAA23.3-14 Eq. 11.3)

SkyCiv Foundation, 式に準拠 3, 一方向せん断ユニティ比を計算します (方程式 4) せん断耐力よりもせん断需要をとることによって.

\( \テキスト{ユニティレシオ} = frac{\テキスト{せん断需要}}{\テキスト{せん断耐力}} \右矢印 \) 方程式 4

双方向せん断

の 双方向せん断 限界状態, としても知られている パンチングシアー, クリティカルセクションをある距離まで拡張します “d / 2” 柱の面から、そして柱の周囲から. 重要なせん断面は、基礎のそのセクションにあります (図を参照してください 2).

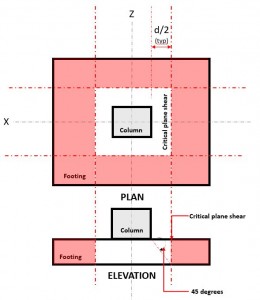
図 2. 双方向せん断の臨界せん断面

の ふたつのやり方需要を聞く または V _f 臨界せん断面で発生します, の距離に位置 “d / 2” どこ (赤) ハッチングエリア, 図に示されている 2, に従って CSAA23.3-14, セクション 13.3.3.

の せん断耐力 または V _c 式を使用して計算された最小値によって決まります。 5, 6, そして 7 あたり CSAA23.3-14, セクション 13.3.4.1

\(\テキスト{V }_{\テキスト{c}} = left ( 1 + \フラク{2}{\ベータ_{\テキスト{c}}} \正しい ) \回 0.19 \回 lambda times phi _{\テキスト{c}} \回 sqrt{f’_{c}} \右矢印 \) 方程式 5 (CSAA23.3-14 Eq. 13.5)

\(\テキスト{V }_{\テキスト{c}} = left ( \フラク{\=最も近いサポートの面までのせん断が考慮されているセクションの距離{\テキスト{s}} \倍 text{d}}{\テキスト{b}_{\テキスト{の}}} + 0.19 \正しい ) \回 lambda times phi _{\テキスト{c}} \回 sqrt{f’_{c}} \右矢印 \) 方程式 6 (CSAA23.3-14 Eq. 13.6)

\(\テキスト{V }_{\テキスト{c}} = 0.38 \回 lambda times phi _{\テキスト{c}} \回 sqrt{f’_{c}} \右矢印 \) 方程式 7 (CSAA23.3-14 Eq. 13.7)

注意: b_c 柱の長辺と短辺の比率です, 集中負荷, または反応面積とα_s によって与えられます 13.3.4.1

どこ:
λ = コンクリート密度の修正係数
f’_c =指定された圧縮コンクリート強度, MPa
d =極端な圧縮繊維から縦方向の張力補強の重心までの距離, んん

CSA A23.3-14 の設計要件を満たすには、せん断需要とせん断耐力が次の式を満たす必要があります。:

\(\テキスト{V }_{\テキスト{f}} \leq phi text{V }_{\テキスト{c}} \右矢印 \) 方程式 8 (CSAA23.3-14 Eq. 11.3)

SkyCiv Foundation, 式に準拠 8, 双方向せん断ユニティ比を計算します (方程式 9) せん断耐力よりもせん断需要をとることによって.

\( \テキスト{ユニティレシオ} = frac{\テキスト{せん断需要}}{\テキスト{せん断耐力}} \右矢印 \) 方程式 9

たわみ

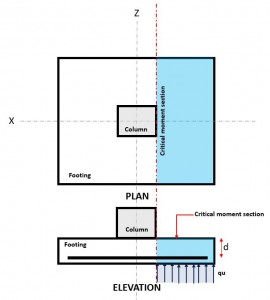
図 3. クリティカルフレクシャセクション

の 曲げ 限界状態が発生するのは クリティカルフレクシャセクション, 基礎の上の柱の面にあります (図を参照してください 3).

の 瞬間的な需要, または M_f クリティカルフレクシャセクションにあります (青いハッチエリア) 図に示されている 3, 方程式を使用して計算されます 10.

\( \テキスト{M}_{あなた} = text{q}_{あなた} \倍左 ( \フラク{l_{バツ}}{2} – \フラク{c_{バツ}}{2} \正しい ) \倍l_{と} \倍左 ( \フラク{\フラク{l_{バツ}}{2} – \フラク{c_{バツ}}{2} }{2} \正しい ) \右矢印 \) 方程式 10

どこ:
q_あなた =因数分解された土壌圧力, kPa
l_バツ = x軸に沿った基礎寸法, んん
l_と = z軸に沿った基礎寸法, んん
c_バツ = x軸に沿った列の寸法, んん

の モーメント抵抗, または Mr 式を使用して計算されます 11.

\( \テキスト{M}_{r} = phi_{\テキスト{s}} \倍A_{s} \倍f_{そして} \倍左( d – \フラク{a}{2} \正しい) \右矢印 \) 方程式 11

どこ:
ϕ_s = ノンプレストレス鉄筋の抵抗係数
d =極端な圧縮繊維から縦方向の張力補強の重心までの距離, んん
あ_s =補強エリア, んん²
a =同等の長方形応力ブロックの深さ, んん
fy =補強強度, MPa

FEA を備えた新しい SkyCiv 財団

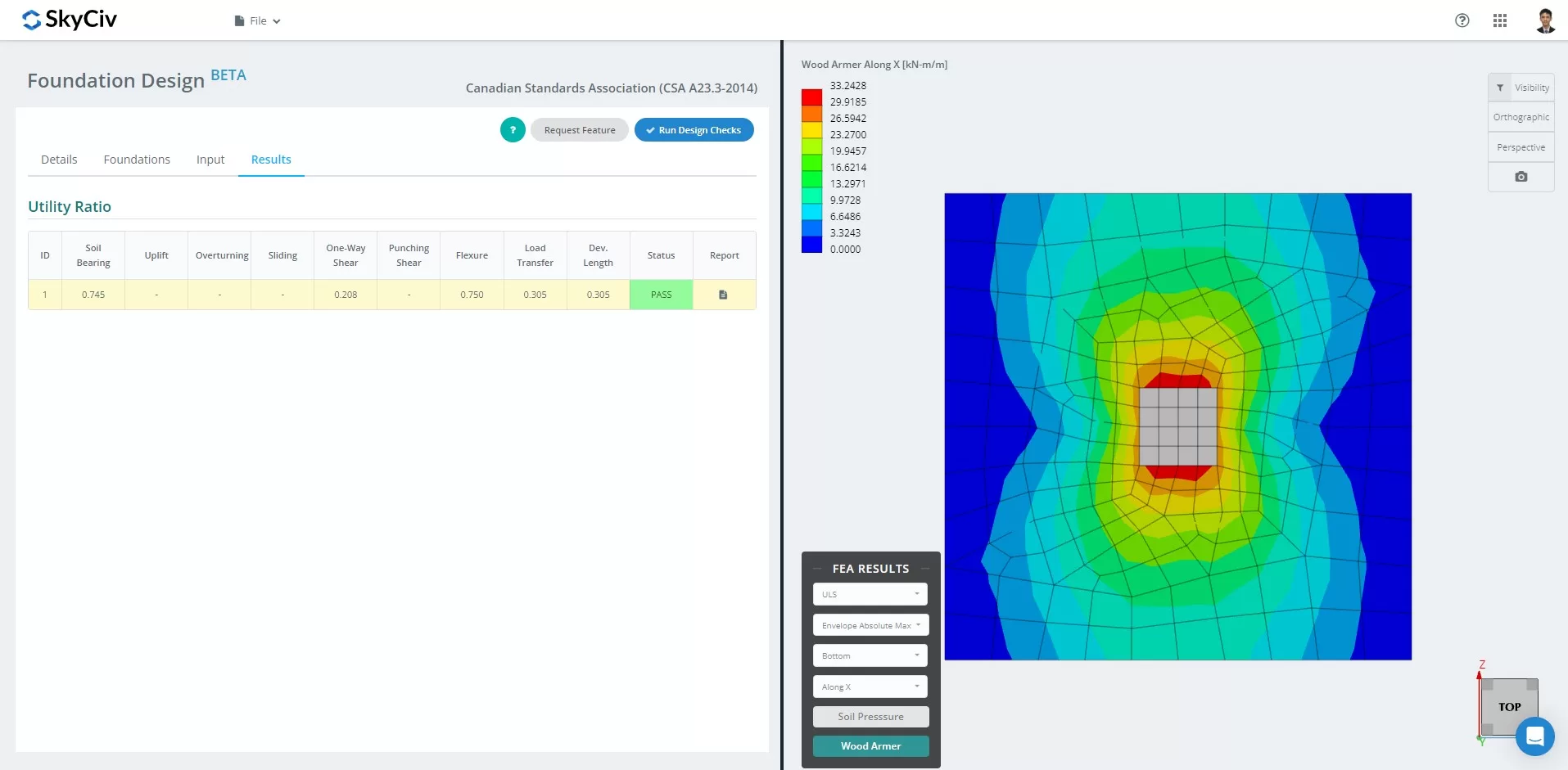
3月現在 2024, Foundation Design モジュールには有限要素解析が統合されています (醜い) ソルバーの機能を調べる. この新機能により、ユーザーは CSA A23.3-14 で指定されたすべての構造チェックを実行しながら、詳細な土圧分析と木材アーマー分析を行うことができます。, 上記のすべての検証を含む. FEA 結果の概要は包括的なレポートに含まれています.