概要概要
曲げ応力は構造設計において最も重要な値の 1 つです, ほとんどの水平梁と同様に、これは通常、重要な設計または支配的な設計です。. 水平ビームが荷重されると, それは生成します 曲げモーメント セクションの上部と下部の繊維に応力がかかり、セクションに過剰な応力がかかり、降伏または完全な破損を引き起こす可能性があります。.
曲げ応力を計算する場合, 次のことを考慮することが重要です:
- セクションの慣性モーメント – 曲げ応力に直接影響します
- ビーム上のどこをチェックしているのか – 通常、曲げ応力はセクションの中立軸から遠ざかるほど増加します。 (したがって、断面の上部と底部で応力が最大になるのはなぜですか)
- 材料特性 – より強力な材料 (たとえば、より高い降伏強度) より高い応力に耐えることができ、特定の設計ではより適切な場合があります
- 断面形状 – ポイントと同じように (1) 上 – さまざまなセクションがより高い曲げ応力に耐えるのに適しています, より高い慣性モーメント値を考慮すると
- 応力の方向 – 荷重の方向に応じて、セクションの長軸と短軸の両方で曲げが発生する可能性があります。.
- 頻繁, これらの曲げ応力は、せん断応力または軸応力と組み合わせることができます。 (他の方向の力により), 梁の全体的な応力を増加させる
次のガイドでは、主に曲げ応力を計算する方法を説明します。 (特にIビームでは), ただし、これらの原則を学ぶ際には、上記の背景を念頭に置くことが重要です。.
梁の曲げ応力を計算する方法?
ビームの曲げはビームの設計において重要な役割を果たすため、曲げ応力を理解することが重要です。. このチュートリアルでは、式を使用して梁の曲げ応力を計算する方法を説明します。. この式は、梁の長手方向の応力分布と内部応力分布を関連付けます。 曲げモーメント 梁の断面に作用. 梁の材料は 線形弾性 (つまり. フックの法則 該当する).
1. 曲げ応力公式を使用して手動で曲げ応力を計算 (方程式)
例を見てみましょう. 以下に示すIビームを検討してください:
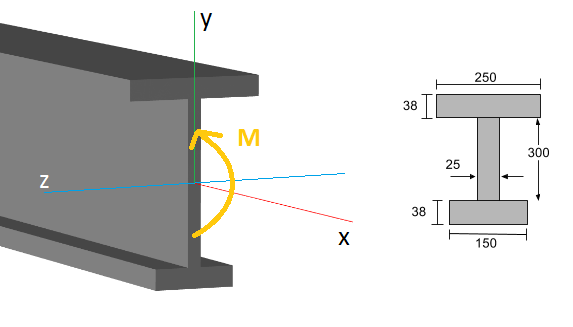
ビームの長さに沿った特定の点で (X軸), 内部曲げモーメントが存在します (M), 通常、曲げモーメント図を使用して決定されます. 一般的な曲げ応力公式 (または通常のストレス) セクションには:
梁の特定のセクションを考慮する場合, 曲げ応力は中立軸から特定の距離で最大値に達することが明らかになりました。 (そして). したがって, 最大曲げ応力は梁セクションの上部または底部で発生します。, どちらの距離が大きいかに応じて:
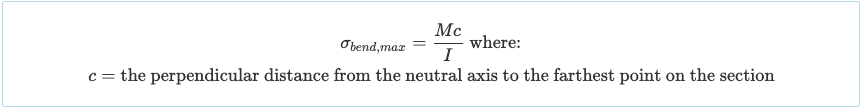
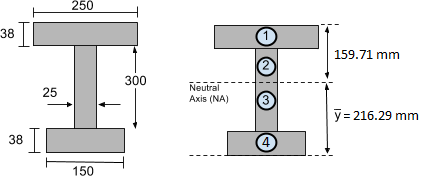
上記の I ビームの実際の例を考えてみましょう. 以前の 慣性モーメントのチュートリアル, 中立軸周りの慣性モーメントはI = 4.74×108 んん4. さらに, の中に 図心チュートリアル, 重心、したがって中立軸の位置が 216.29 セクションの下部からmm. これを以下に示します:
通常、セクションが受ける最大曲げ応力を決定する必要があります。. 例えば, 決定したと仮定しましょう, 曲げモーメント線図より, ビームが最大曲げモーメントに遭遇すること 50 kN-mまたは 50,000 Nm (曲げモーメント単位を変換した後).
次に、セクションの上部または下部が中立軸から離れているかどうかを見つける必要があります。. 明らかに, セクションの下部の距離が長くなります, c = の測定 216.29 んん. この情報により, 上記の曲げ応力公式を使用して、最大応力の計算に進むことができます。:
同様に, セクションの上部に曲げ応力が見つかりました, y =であることを知っているので 159.71 中立軸からのmm (NA):
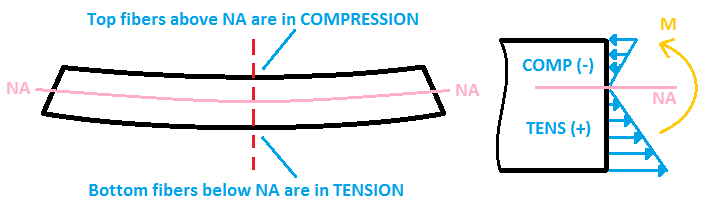
最終的な考慮事項には、ビーム応力が断面の繊維の圧縮または張力を引き起こしているかどうかを判断することが含まれます。.
- ビームが次のように垂れ下がっている場合 “U” 形, 上部の繊維は圧縮を受けます (負のストレス), 底部の繊維には張力がかかります (正のストレス).
- ビームが逆さまにたわむ場合 “U” 形, 状況は逆転した: 底部の繊維は圧縮されます, 上部の繊維には張力がかかります.
2. ソフトウェアを使用して曲げ応力を計算する
上のセクションでは、手作業で計算するための曲げ応力公式について説明しました。, しかし、もう自分で手動で行う必要はありません。 SkyCivビーム計算機 ワンクリックで梁のせん断応力と曲げ応力を見つけることができます。. 単純にビームをモデリングするだけで, サポートを組み込む, そして負荷をかける, この曲げ応力計算ツールを使用して最大応力を取得できます。. 以下の画像は、曲げ応力が発生しているI型梁の例を示しています:
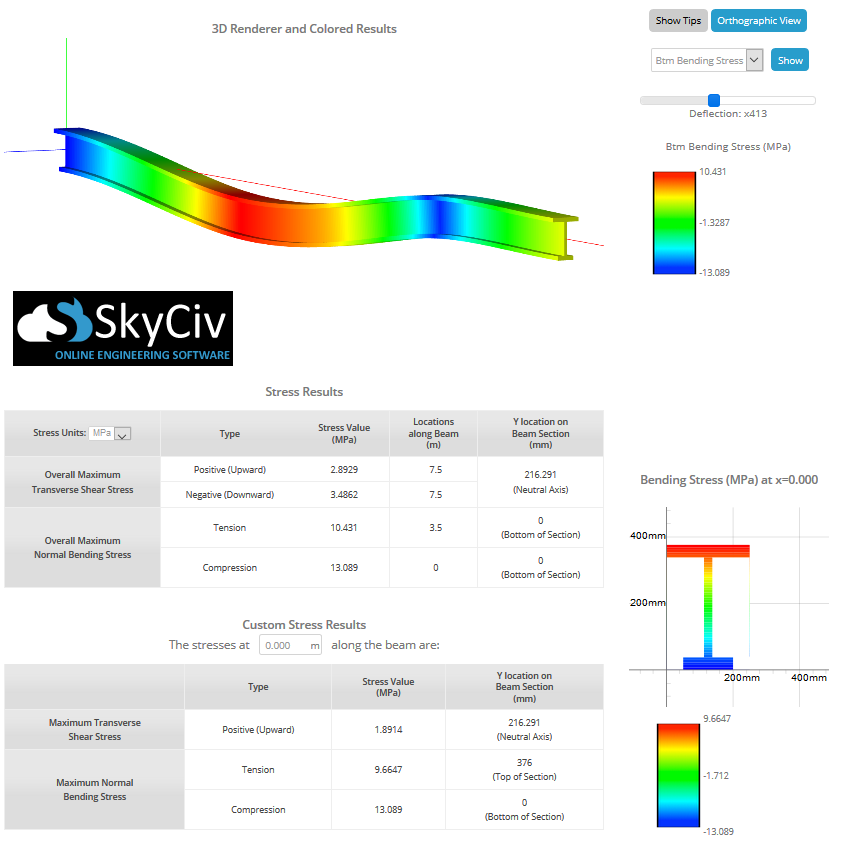
ユーザーは以下も使用できます ビーム応力ソフトウェア 曲げ応力およびその他のビーム応力を計算する, シンプルなセクション作成ツールを使用する. 上記のビーム ツールをチェックするか、今すぐサインアップしてソフトウェアを無料で体験してください!
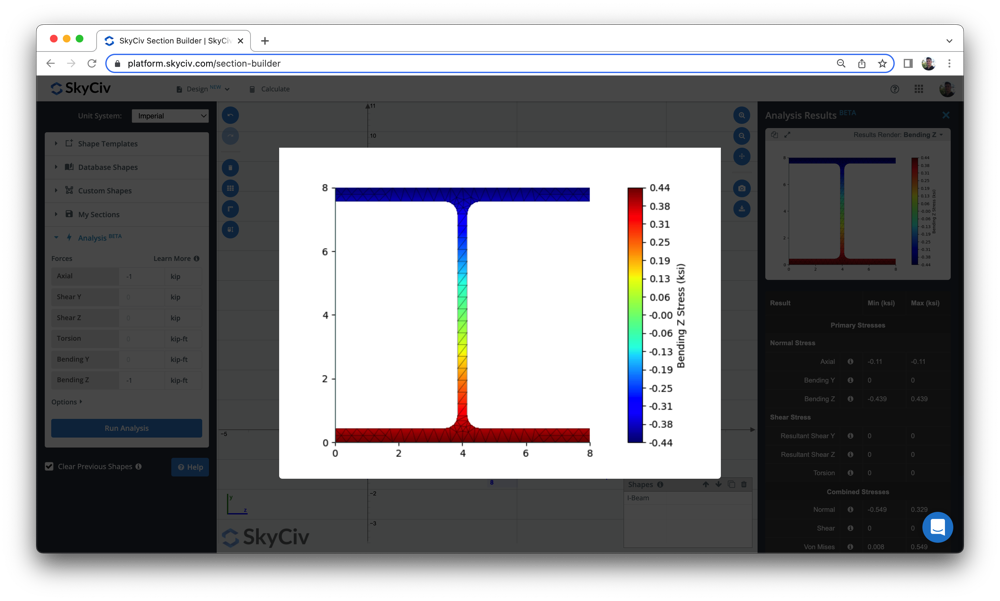
ビームに関するその他のドキュメントについては、, に関する記事をご覧ください 梁断面の曲げ応力の計算, 曲げモーメントを求める方法, サポートでの反応を判断する, そして ビーム偏向.
