重心の基礎
断面に注意することが重要です, その面積は全体的に均一です, 重心は、任意に設定された軸に関するモーメントの合計を取ることによって見つけることができます, 通常は上部または下部のファイバーに設定されます. についての以前の記事をご覧ください。 この記事では、図心を計算する簡単なプロセスについて説明します。 ビーム断面と SkyCiv 無料重心計算機.
基本的に, 重心は、面積の合計に対するモーメントの合計を取ることによって取得できます. このように表現されています.
[数学]
\バー{バツ}= frac{1}{あ}\int xf left ( x右 )dx
[数学]
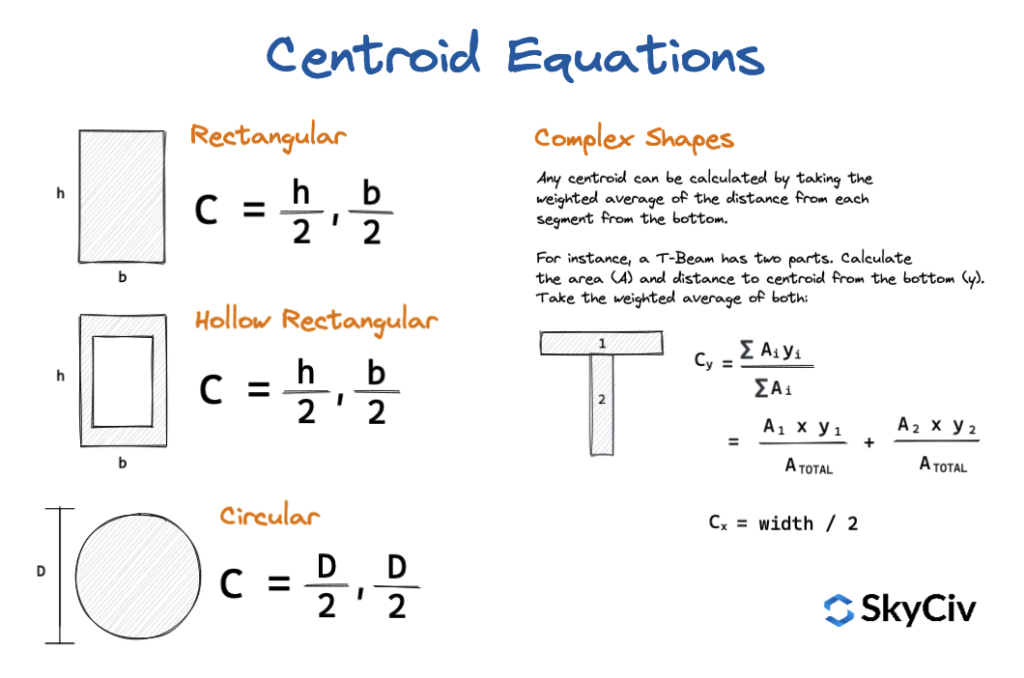
重心方程式のまとめ
上記の方程式で, f(バツ) は関数、xはモーメントアーム. これをよりよく説明するために, ベースがx軸と一致する任意の三角形のy重心を導出します. この状況では, 三角形の形, 正反対かどうか, 二等辺または斜角は、すべてがx軸のみに関連しているため、無関係です。. 三角形の底辺が軸に対して一致または平行である場合、形状は無関係であることに注意してください. これは、xセントロイドを解く場合には当てはまりません。. 代わりに, あなたはそれをy軸に対して2つの直角三角形の重心を得ると想像することができます. 便宜上, 以下の参照表のような二等辺三角形を想像してみましょう. b と h の関係を求めると、次の関係が得られます。.
[数学]
\フラク{-そして}{バツ}= frac{-h}{b}
[数学]
三角形が直立していると想像しているので、傾きは負であることに注意してください. 三角形が反転することを想像すると, 勾配は正になります. とにかく, 関係は変わらない. x = fとして(そして), 上記の関係は次のように書き直すことができます.
[数学]
x = f left ( y right )= frac{b}{h}そして
[数学]
重心を解くことができます. 上記の最初の方程式を調整する, 私たちは以下を得ます.
[数学]
\バー{そして}= frac{1}{あ}\int yf left ( y right )二
[数学]
追加の値を差し込み、上記の関係を代入すると、次の方程式が得られます.
[数学]
\バー{そして}= frac{2}{bh}\int_{0}^{h} \フラク{b}{h}そして^{2}二
[数学]
単純化,
[数学]
\バー{そして}= frac{2}{h ^{2}}\左 [ \フラク{そして^{3}}{3} \正しい ]_{0}^{h}
[数学]
[数学]
\バー{そして}= frac{2}{h ^{2}}\左 [ \フラク{h ^{3}}{3}-0 \正しい ]
[数学]
[数学]
\バー{そして}= frac{2}{3}h
[数学]
このソリューションは上から取られていることに注意してください. 下から取られた重心は、次に等しくなければなりません 1/3 の.
一般的な形状とビーム断面の図心を求める公式
以下は、 さまざまなビーム断面形状 およびセクションの重心までの距離. 方程式は、特定のセクションの重心をセクションのベースまたは左端のポイントから見つける方法を示します. SkyCiv StudentおよびStructuralサブスクリプションの場合, このリファレンスは、PDFリファレンスとしてダウンロードして、どこにでも持って行くことができます. ビームセクションの図心は、中立軸を特定するため非常に重要であり、ビームセクションを分析するときに必要な最も早いステップの1つです。.
SkyCivはまた、ビームセクションに関連するすべての方程式と式を含むセクションテーブルの包括的な概要を提供します (慣性モーメント, エリアなど…).
さまざまな重心の方程式を以下に示します:
| 参照 | Cそして (下からの距離) |
Cバツ (一番左の点からの距離) |
長方形または長方形断面の重心 |
||
|---|---|---|
 |
[数学] \dfrac{h}{2} [数学] |
[数学] \dfrac{b}{2} [数学] |
中空長方形断面の重心 |
||
 |
[数学] \dfrac{b}{2} [数学] |
[数学] \dfrac{h}{2} [数学] |
円または円形断面の重心 |
||
 |
[数学] \dfrac{D}{2} [数学] |
[数学] \dfrac{D}{2} [数学] |
中空円形断面の重心方程式 |
||
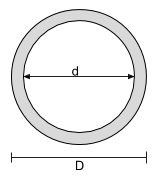 |
[数学] \dfrac{D}{2} [数学] |
[数学] \dfrac{D}{2} [数学] |
二等辺三角形の重心 |
||
 |
[数学] \dfrac{h}{3} [数学] |
[数学] \dfrac{b}{2} [数学] |
I ビームの重心 |
||
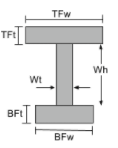 |
[数学] \フラク{TFw times TFt times left ( BFt + Wh + \フラク{TFt}{2} \正しい )}{TFw times TFt + Wt times Wh + BFw times BFt} + [数学] [数学] \フラク{Wt times Wh times left ( BFt + \フラク{Wh}{2} \正しい )}{TFw times TFt + Wt times Wh + BFw times BFt} + [数学] [数学] \フラク{BFw times BFt times left ( \フラク{BFt}{2} \正しい )}{TFw times TFt + Wt times Wh + BFw times BFt} [数学] |
[数学] TFw > BFw, \フラク{TFw}{2}[数学] [数学] BFw > TFw, \フラク{BFw}{2} [数学] |
T断面の図心 |
||
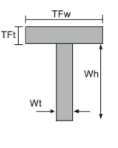 |
[数学] \フラク{Wt times Wh times left ( \フラク{Wh}{2} \正しい )}{TFw times TFt + Wt times Wh } + [数学] [数学] \フラク{TFw times TFt times left ( Wh + \フラク{TFt}{2} \正しい ) }{TFw times TFt + Wt times Wh } [数学] |
[数学] \フラク{TFw}{2} [数学] |
C断面の重心 |
||
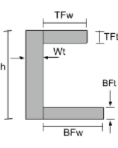 |
[数学] \フラク{TFw times TFt times left ( h – \フラク{TFt}{2} \正しい )}{TFw times TFt + Wt times Wh + BFw times BFt} + [数学] [数学] \フラク{Wt times h times left ( \フラク{h}{2} \正しい )}{TFw times TFt + Wt times Wh + BFw times BFt} + [数学] [数学] \フラク{BFw times BFt times left ( \フラク{BFt}{2} \正しい )}{TFw times TFt + Wt times Wh + BFw times BFt} [数学] |
[数学] \フラク{TFt times TFw times left ( Wt + \フラク{TFw}{2} \正しい )}{TFt times TFw + h times Wt + BFt times BFw} + [数学] [数学] \フラク{h times Wt times left ( \フラク{Wt}{2} \正しい )}{TFt times TFw + h times Wt + BFt times BFw} + [数学] [数学] \フラク{BFt times BFw times left ( Wt + \フラク{BFw}{2} \正しい )}{TFt times TFw + h times Wt + BFt times BFw} [数学] |
角の重心 |
||
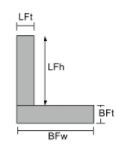 |
[数学] \フラク{LFt times LFh times left ( BFt + \フラク{LFh}{2} \正しい ) }{LFt times LFh + BFw times BFt} + [数学] [数学] \フラク{BFw times BFt times left ( \フラク{BFt}{2} \正しい )}{LFt times LFh + BFw times BFt} [数学] |
[数学] \フラク{LFh times LFt times left ( \フラク{LFt}{2} \正しい )}{LFh times LFt + BFt times BFw} + [数学] [数学] \フラク{BFt times BFw times left ( \フラク{BFw}{2} \正しい )}{LFh times LFt + BFt times BFw} [数学] |
ビームの重心の自動計算式
私たちをチェックしてください この記事では、図心を計算する簡単なプロセスについて説明します。, の簡易版 SkyCivセクションビルダー, 手計算を必要とせずにビームの重心を自動的に計算します. または今すぐサインアップして始めましょう!


