慣性モーメントの基礎
慣性モーメントは次のように導出されます。 慣性モーメント 部品の分割と伝達公式の適用: I = I0 + 広告2. へのアプローチを説明した包括的な記事があります。 慣性モーメントを解決する.
基本的に, 慣性モーメントは断面二次モーメントです, これは次のように表すことができます:
[数学] 私_{バツ}= int int y ^{2}与える [数学] [数学] 私_{そして}= int int x ^{2}与える [数学]
以下の式の導出を観察するには, 上記の式だけを使用して、長軸を中心とした長方形などのオブジェクトの慣性モーメントを見つけようとします。. 慣性モーメントを取得するには, 限界は、回転軸からその極端な繊維までとられるように決定する必要があります. これが外側の積分の限界になります. 内側の積分には 0 bへ. とはいえ, dAをxdyとして表現することもできます, これはbdyになります. 回転軸が中立軸にあるので, 慣性モーメントは、上限h / 2および下限と統合できます。 0 長方形の対称性のために2倍になります. これにより、以下の積分が残ります.
[数学] 私_{バツ}= 2 int_{0}^{\フラク{h}{2}} そして^{2}bdy [数学] 統合, [数学] 私_{バツ}= 2b left [ \フラク{そして^{3}}{3} \正しい ]_{0}^{\フラク{h}{2}} [数学] [数学] 私_{バツ}= 2b left [ \フラク{h ^{3}}{24}-0 \正しい ] [数学] [数学] 私_{バツ}= frac{bh ^{3}}{12} [数学]
梁断面の慣性モーメントの計算式
SkyCiv は、ビームセクションの慣性モーメント方程式の概要をまとめました。 (断面二次モーメント). 慣性モーメント方程式は、高速で正確な計算に非常に役立ちます. 数式は、便宜上、最も単純な形式にまとめられています。.
SkyCivはまた提供します 慣性モーメントの計算機 すばやく計算したり、数式が正しく適用されていることを確認したりするために. 長方形の慣性モーメントの式, サークル, 中空ビームと三角ビームのセクションが与えられています. ビームの断面慣性モーメントに関して覚えておくべき重要な点は次のとおりです。:
- 断面二次モーメントは質量慣性モーメントとは異なります
- 断面二次モーメントとしても知られています
- それはたわみの重要な要因です (私が大きいほどバツ, より低いたわみは)
- 単位の長さはの累乗です 4
- 以下の方程式は、断面の図心に関する慣性モーメントを示しています。
参照 |
私xx |
私yy |
長方形または長方形断面の慣性モーメント方程式 |
||
|---|---|---|
 |
[数学] \dfrac{bh ^ 3}{12} [数学] | [数学] \dfrac{b ^{3}h}{12} [数学] |
中空長方形断面の慣性モーメント方程式 |
||
 |
[数学] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [数学] | [数学] \dfrac{b ^ 3h}{12} – \dfrac{b_1 ^ 3h_1}{12} [数学] |
円または円形セクションの慣性モーメント方程式 |
||
 |
[数学] \dfrac{\パイ}{64}D ^ 4 [数学] | [数学] \dfrac{\パイ}{64}D ^ 4 [数学] |
中空円形断面の慣性モーメント方程式 |
||
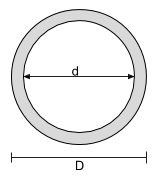 |
[数学] \dfrac{\パイ}{64}D ^ 4 – \dfrac{\パイ}{64}d ^ 4 [数学] | [数学] \dfrac{\パイ}{64}D ^ 4 – \dfrac{\パイ}{64}d ^ 4 [数学] |
二等辺三角形の慣性モーメント方程式 |
||
 |
[数学] \dfrac{bh ^ 3}{36} [数学] | [数学] \dfrac{3b ^ 3h}{144} [数学] |
Iセクションの慣性モーメント方程式 |
||
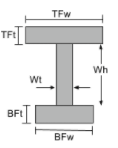 |
[数学] \フラク{TFw times TFt ^{3}}{12} +\フラク{Wt times Wh ^{3}}{12} + \フラク{BFw times BFt ^{3}}{12} +[数学] [数学] TFw times TFt times left ( BFt + Wh + frac{TFt}{2} -\バー{そして}_{ボット} \正しい )^{2} +[数学] [数学] Wt times Wh times left ( BFt + frac{Wh}{2} -\バー{そして}_{ボット} \正しい )^{2} +[数学] [数学] BFw times BFt times left ( \フラク{Wh}{2} -\バー{そして}_{ボット} \正しい )^{2} [数学] | [数学] \フラク{TFt times TFw ^{3}}{12} + \フラク{Wh times Wt ^{3}}{12} + \フラク{BFt times BFw ^{3}}{12} [数学] |
T断面の慣性モーメント方程式 |
||
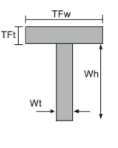 |
[数学] \フラク{TFw times TFt ^{3}}{12} + \フラク{Wt times Wh ^{3}}{12} +[数学] [数学] TFw times TFt left ( Wh + \フラク{TFt}{2} -\バー{そして}_{ボット} \正しい )^{2} +[数学] [数学] Wt times Wh times left ( \フラク{Wh}{2} – \バー{そして}_{ボット} \正しい )^{2} [数学] | [数学] \フラク{TFt times TFw ^{3}}{12} + \フラク{Wh times Wt ^{3}}{12} [数学] |
チャネルセクションの慣性モーメント方程式 |
||
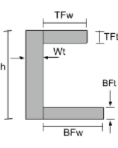 |
[数学] \フラク{TFw times TFt ^{3}}{12} + \フラク{BFw times BFt ^{3}}{12} + \フラク{Wt times h ^{3}}{12} +[数学] [数学] TFw times TFt times left ( h – \フラク{TFt}{2} – \バー{そして}_{ボット} \正しい )^{2} +[数学] [数学] BFw times BFt times left ( \フラク{BFt}{2} – \バー{そして}_{ボット} \正しい )^{2} +[数学] [数学] Wt times h times left ( \フラク{h}{2} – \バー{そして}_{ボット} \正しい )^{2} [数学] | [数学] \フラク{TFt times TFw ^{3}}{12} + \フラク{BFt times BFw ^{3}}{12} + \フラク{h times Wt ^{3}}{12} +[数学] [数学] TFt times TFw times left ( Wt + \フラク{TFw}{2} – \バー{バツ}_{左} \正しい )^{2} +[数学] [数学] BFt times BFw times left ( Wt + \フラク{BFw}{2} – \バー{バツ}_{左} \正しい )^{2} +[数学] [数学] h times Wt times left ( \フラク{Wt}{2} – \バー{バツ}_{左} \正しい )^{2} [数学] |
慣性モーメントの角度方程式 |
||
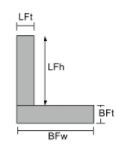 |
[数学] \フラク{BFw times BFt ^{3}}{12} + \フラク{ LFt times LFh ^{3}}{12} +[数学] [数学] BFw times BFt times left ( \フラク{BFt}{2}-\バー{そして}_{ボット} \正しい )^{2} +[数学] [数学] LFt times LFh times left ( BFt + \フラク{LFh}{2}-\バー{そして}_{ボット} \正しい )^{2} [数学] | [数学] \フラク{BFt times BFw ^{3}}{12} + \フラク{ LFh times LFt ^{3}}{12} +[数学] [数学] BFt times BFw times left ( \フラク{BFw}{2}-\バー{バツ}_{左} \正しい )^{2} +[数学] [数学] LFh times LFt times left ( \フラク{LFt}{2}-\バー{バツ}_{左} \正しい )^{2} [数学] |
手計算にSkyCivセクションビルダーを使用する
記事上で, 慣性モーメントの公式について説明しました。. このトピックの詳細については、, のチュートリアルにアクセスしてください 梁部の慣性モーメント.
知ってますか SkyCivセクションビルダー 次の形状のフルハンド計算も示しています。?
- 長方形, 中空長方形
- 円形, 中空円形
- アイビーム, Tビーム
- 角度 (Lビーム), チャネル
- 三角形のセクション
上記の表が、円の慣性モーメントの計算方法に役立つことを願っています。, 三角形, 他の形状の中でも長方形の慣性モーメント. 便利なものもあります 慣性モーメント計算機, の簡略化 SkyCivセクションビルダー, これらの計算を自動的に処理するか、今すぐサインアップして SkyCiv ソフトウェアの使用を開始してください!


