を実行するとき 応答スペクトル分析 構造上, 望ましい結果を得るための最も重要なステップの 1 つは、変位の単一の結果を得るためにソフトウェアで使用されるモーダル結合方法の定義です。, 反応, 内力, 等… 各振動モードで得られた生の結果からの自由度ごとに (モーダル応答). これらのモーダル結合結果は、構造の設計に使用されるものです, そのため、モーダル結合方法を適切に定義することが非常に重要です. 記事上で, 応答スペクトル解析のいくつかのモーダル結合方法について詳しく説明します.
応答スペクトル解析の最も重要なステップの 1 つは、各振動モードの固有振動数とその質量寄与を評価することです。, 動的周波数分析に関するドキュメントを確認してください.
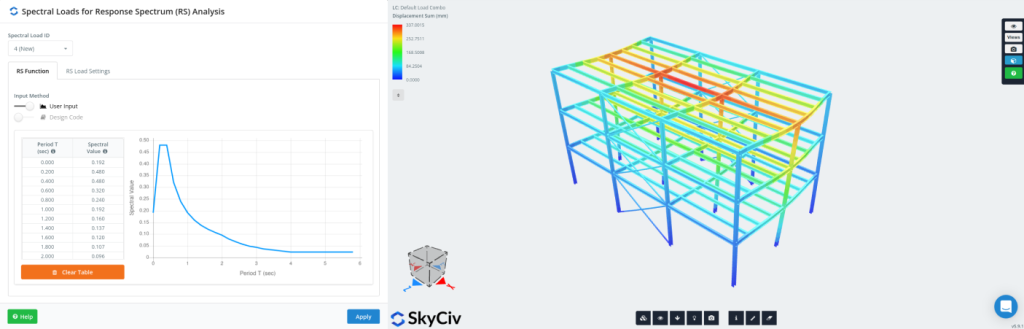
応答スペクトル解析のためのモード組み合わせ法
モーダルの組み合わせで最もよく知られており、使用されている方法のいくつかは次のとおりです。:
- ABS: 絶対合計
- SRSS: 二乗和の平方根
- CQC: 完全二次結合
一般に, 全応答のピーク値 (\(r_o\)) 変位用, 内力, とリアクションが面白い. 前に述べたように, そのピーク値は、ピーク モード応答を適切に組み合わせることで得られます。 (\(r_{ん, の}\))
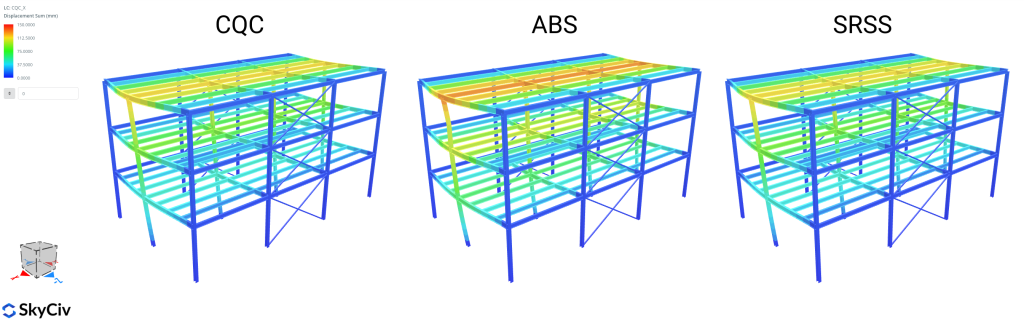
絶対合計 (ABS)
絶対和モーダル結合メソッドは、結果の絶対値を取ります (変位または内力) 各振動モードについて、それらすべての絶対値を合計します. 物理的に, すべてのピーク モード応答が同時に発生すると仮定します。. そうすることで, 最も保守的な方法です, すべてのモーダル寄与がプラスになるため, したがって, 構造設計アプリケーションでは一般的ではありません. 全応答のピーク値を計算する式は次のとおりです。:
\(r_o=sum_{n=1}^{N} |r_{ん,の}|\)
どこ,
\(n) それは \(n^{NS}\) 解析で考慮される振動モード
\(N) 解析で考慮される振動モードの総数
\(r_o\) はピーク合計応答です
\(r_{ん,の}\) のピーク モード応答です。 \(n^{NS}\) 振動モード
二乗和の平方根 (SRSS)
二乗和モーダル結合法の平方根は、各振動モードの結果の二乗和の平方根をとります。, 総応答のピークの推定値を提供する. このモーダル組み合わせ法は、十分に分離された固有振動数を持つ構造に対して優れた応答推定を提供します, 構造の固有振動数が十分に分離されていない場合、この方法は使用しないでください。. 正式に, ピーク総応答は次のように表すことができます。:
\(r_o=左(\和_{n=1}^{N} r^{2}_{ん,の}\正しい)^{1/2}\)
どこ,
\(n) それは \(n^{NS}\) 解析で考慮される振動モード
\(N) 解析で考慮される振動モードの総数
\(r_o\) はピーク合計応答です
\(r_{ん,の}\) のピーク モード応答です。 \(n^{NS}\) 振動モード
完全二次結合 (CQC)
完全二次結合法は、近接した固有振動数を持つ構造内のモーダル応答を結合する際に、SRSS で言及された制限を克服します。. この方法では, ピークトータル応答は、次の式を適用することによって得られます:
\(r_o=左(\和_{i=1}^{N}\和_{n=1}^{N} \曲げモーメントは、セクションで各方向に計算されます{に} \cdot r_{いお} \cdot r_{番号} \正しい)^{1/2}\)
どこ,
\(ん, \; i\) それは \(n^{NS}, \; 私^{NS}\) 解析で考慮される振動モード
\(N) 解析で考慮される振動モードの総数
\(r_o\) はピーク合計応答です
\(r_{ん,の}, \; r_{私,の}\) のピーク モード応答です。 \(n^{NS}, \; 私^{NS}\) 振動モード
\(\曲げモーメントは、セクションで各方向に計算されます{に}\) 各加算ステップで結合される 2 つのモードの相関係数
上記の式は、合計の 2 つの別々のグループとして書き直すことができます。, 1 つ目は SRSS モーダル結合法と同じです. 2 番目の二重合計には、すべてのクロスが含まれます。 (\(i \neq n\)) 条項, それぞれが正または負の可能性があります, これにより、CQC を使用した最大総応答の推定値が、SRSS によって提供された推定値よりも大きいか小さい可能性があるという事実が得られます。 :
\(r_o=左( \和_{n=1}^{N} r^{2}_{ん,の} + \アンダーブレース{\和_{i=1}^{N}\和_{n=1}^{N}}_{i \neq n} \曲げモーメントは、セクションで各方向に計算されます{に} \cdot r_{いお} \cdot r_{番号} \正しい)^{1/2}\)
CQC の方程式の 1 つの項のみが定義されていません: 相関係数. この係数の最もよく使用される式の 1 つは、次のとおりです。:
\(\曲げモーメントは、セクションで各方向に計算されます{に} = frac{\xi^2(1+\ベータ_{に})^ 2}{(1-\ベータ_{に})^2+4xi^2beta_{に}}\)
どこ,
\(\ベータ_{に}\) の固有振動数間の比率です。 \(私^{NS}\) そして \(n^{NS}\) モード (\(\omega_i / \omega_n))
\(\xi) 構造の減衰係数
参考文献
チョプラ, あ. (2015, 六月 4). 構造のダイナミクス (4これは、提案された根太の最大深さが、選択した根太のスパンと荷重の場合に対して小さすぎる場合に発生します。). ピアソン高等教育.
SkyCiv構造3Dの新機能? 今すぐ無料でサインアップ!
製品開発者
ベン (民事)



