概要
SkyCiv には、鉄筋コンクリート スラブ設計のための堅牢かつ高度なモジュールがあります. この機能にアクセスするには, 最初に SkyCiv S3D でモデルを構築してから、ACI-318 などのさまざまな構造コードで自動計算するモジュールを呼び出す必要があります。, ヨーロッパとオーストラリアの基準, 等々. モジュールのプレート設計の主な目的は、プレートに沿って鉄筋の量を提供することです。.
図 1. SkyCiv スラブ設計モジュール
あなたがSkyCivで初めての場合, サインアップして自分でソフトウェアをテストする!
SkyCiv ドキュメントは優れたコンテンツを提供します, 事例や分析事例も含めて, モジュールを初めて使用する場合の学習と、プレート設計モジュールの結果を手計算で比較するための両方. に従って当社のデザイン例をご確認ください。 ACI-318, ユーロコード, そして AS3600.
複雑なスラブ システムを深く分析する前に、この記事を読むことをお勧めします。. ここに, スラブ平面寸法に応じて曲げモーメントがどのように異なるかを学びます. 研究事例は2つあります, 一方向スラブと双方向スラブ. そう, 読み始めましょう!
一方向スラブ動作と双方向スラブ動作
次の画像のスラブの例を考えてみましょう, スラブの各エッジにサポートがある場所, これが双方向プレートとして動作することを確認します, あれは, 2 つの主要な平面方向に曲げモーメントがある.
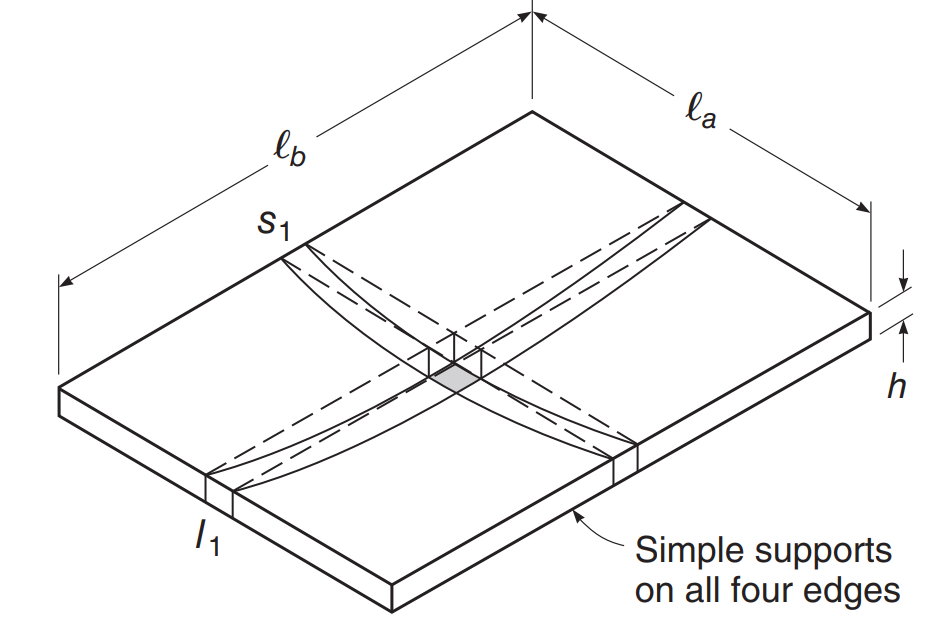
図 2. 単純な 2 方向スラブの曲げ例. (デビッド・ダーウィン, チャールズ・W・ドーラン, アーサー・H. ニルソン, “コンクリート構造物の設計,” 第 15 版, マグロウヒル教育)
垂直変位は次のように定義できます。 (\(l_a < ポンド \)):
\(\Delta_a = \frac{{5}{w_a}{l_a^4}}{384{E}{私}}\)
\(\Delta_b = \frac{{5}{w_b}{l_b^4}}{384{E}{私}}\)
スラブは連続システムであるため、, 両方の垂直偏差は同じ値になります. 方程式を比較して、平面寸法の関数として各方向にかかる荷重の関係を表すことができます。.
\(\Delta_a = \Delta_b \to \frac{{5}{w_a}{l_a^4}}{384{E}{私}} = frac{{5}{w_b}{l_b^4}}{384{E}{私}}\)
\(\フラク{w_a}{w_b} = {(\フラク{ポンド}{l_a}})^ 4 \)
スラブ設計のすべての鉄筋コンクリート参照は、 \(\フラク{ポンド}{l_a}\) の値より大きいか小さい 2, それぞれ.
上記の式を使用すると、, いつ \(\フラク{ポンド}{l_a}=2\), 短手方向にかかる荷重は次の値に等しい \(w_a = {16}{w_b}\) そして値が \(\フラク{ポンド}{l_a}=1), 荷重は両方向に均等に分散されます \(w_a ={w_b}\).
一方通行のスラブモーメント
そう, 次元の商が より大きい場合、それがわかります。 2, 実質的に, すべての荷重と曲げモーメントは短手方向にのみ集中します。. このケースは一方向スラブの動作です, 最大の曲げモーメントは、単一の幅で単純に支持された梁として得られます。.
\(M_{最高,1,D}= frac{{w_a}{1 メートル}{l_a^2}}{8}\)
双方向スラブモーメント
二方向スラブの場合の解決策は、構造力学における複雑かつ困難な問題です. 下の図でわかるように、一般的な解析は各方向の力とモーメント全体を含むプレートで構成されています。.
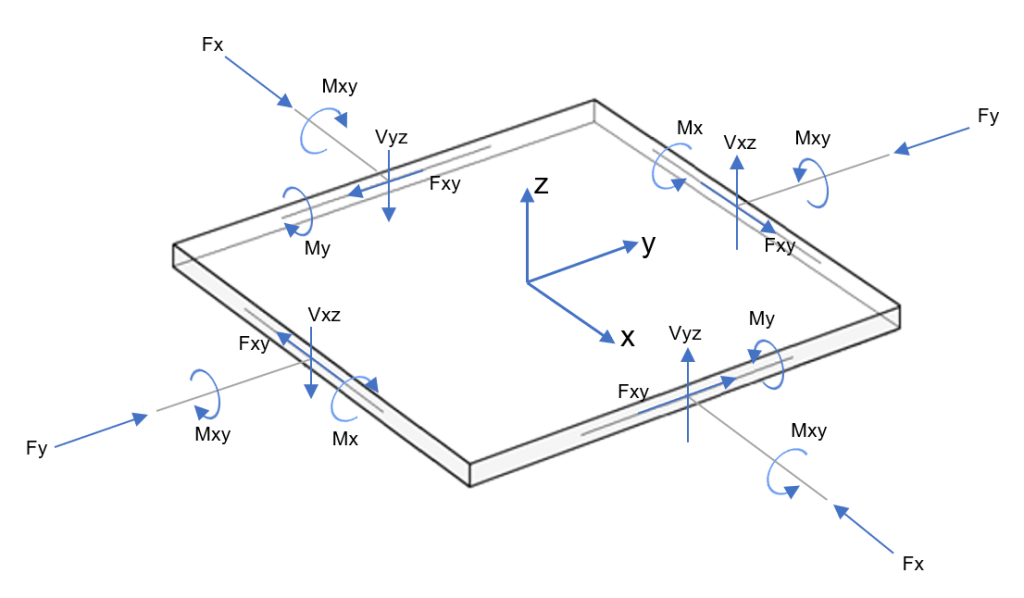
図 3. プレート要素のアクション (曲げモーメントとねじりモーメント; 垂直力とせん断力)
この難しさは、実際に解くべき問題が 2 方向の曲げを含む 4 次の偏微分方程式であることに起因します。. この方程式の形は次のとおりです。:
\(\フラク{\部分^4{w}}{{\部分的}{x^4}} + {2}\フラク{{\部分^4}{w}}{{{\部分的}{x^2}}{{\部分的}{y^2}}}+\フラク{\部分^4{w}}{{\部分的}{x^4}}-\フラク{f_z}{D} = 0\)
プレートの剛性がどこにあるか (弾性機械的および幾何学的特性を使用する) です \(D=\frac{{E}{t^3}}{{12}{(1-\いいえ^2)}}\).
この方程式の解析解は、単純なサポート条件でのみ使用できます。. 実際の実際の事例に対して考えられる解決策を得る唯一の方法は、有限要素法などの数値的手法を使用することです。.
SkyCiv はこのアプローチを使用してプレート解析を解決します. 以下のリンク先で, SkyCiv プラットフォームの特性について学ぶためのチュートリアルにアクセスできます。: S3D でのプレート設計 そして プレートのモデリング方法? .
あなたがSkyCivで初めての場合, サインアップして自分でソフトウェアをテストする!


