ビーム断面の重心または質量中心は、せん断やせん断などの計算に慣性モーメントが必要な場合のビーム解析に役立ちます。曲げ応力 そして 偏向. この記事では、セントロイドを計算する方法の簡単なプロセスについて説明し、SkyCiv Free Centroid Calculator を紹介します.
この記事では、図心を計算する簡単なプロセスについて説明します。
この記事では、図心を計算する簡単なプロセスについて説明します。, この記事では、図心を計算する簡単なプロセスについて説明します。. ビーム断面は通常、1つ以上の形状で構成されています. ビーム断面領域全体の重心を見つけるには, 最初に適切なセグメントに分割する必要があります. この後, セクション全体の重心を見つけるには、個々のセグメントの面積と重心を考慮する必要があります。.
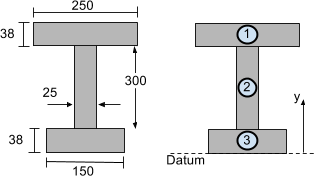
以下に示すIビームのセクションを検討してください. 垂直重心を計算するには (Y方向) に分割することができます 3 図のようなセグメント:
ここで、垂直方向を見つけるために重心方程式を使用するだけです。 (そして) マルチセグメント形状の図心:

ビームセクションの下部からデータムまたは参照線を取得します. では、Aを見つけましょう私 そしてy私 上記のIビーム断面の各セグメントについて、垂直またはyの重心を見つけることができます.
[数学]
\テキスト{セグメント 1:}\\
\ベギン{揃える}
{あ}_{1} &= 250 times38 = 9500 {\テキスト{ んん}}^{2}\\
{そして}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \テキスト{ んん}\\\\
\終わり{揃える}
[数学]
[数学]
\テキスト{セグメント 2:}\\
\ベギン{揃える}
{あ}_{2} &= 300 times25 = 7500 {\テキスト{ んん}}^{2}\\
{そして}_{2} &= 38 + \tfrac{300}{2} = 188 \テキスト{ んん}\\\\
\終わり{揃える}
[数学]
[数学]
\テキスト{セグメント 3:}\\
\ベギン{揃える}
{あ}_{3} &= 38 times150 = 5700 {\テキスト{ んん}}^{2}\\
{そして}_{3} &= tfrac{38}{2} = 19 text{ んん}\\\\
\終わり{揃える}
[数学]

断面が2つの材料または複合材料で構成されている場合, 次に、方程式全体が均一になるように、材料の1つにモジュラー比を掛ける必要があります。.
[数学]
n = frac{E_{1}}{E_{2}}
[数学]
通常, E1 非優勢材料の弾性係数です, およびE2 一般的な材料の弾性係数です, どちらの優先順序が重心の解に影響を与えることはありませんが. 2番目の材料の調整, この記事では、図心を計算する簡単なプロセスについて説明します。.
[数学]
\バー{そして}= frac{\和{あ}_{私}{そして}_{私}+\和 {ん}{あ}_{私}{そして}_{私}}{\和{あ}_{私}+\和 {ん}{あ}_{私}}
[数学]
SkyCivでビームの重心を見つける
ビームの重心を見つけることは重要ですが、手動で計算するのは時間がかかる場合があります. SkyCivは提供しています この記事では、図心を計算する簡単なプロセスについて説明します。 このプロセスを自動化します, 垂直方向を見つけるのに役立ちます (そして) そして水平 (バツ) ビーム断面の重心を簡単かつ正確に測定!
このツールはの無料版です SkyCivセクションビルダー, 幾何学的形状を解析するための包括的なオンライン断面解析ソフトウェア, 曲げ, せん断およびねじりセクションのプロパティ、およびFEAと鉄筋コンクリートの設計. このツールを使用すると, 定義済みのテンプレートを使用してカスタム セクションを作成したり、ポイントを使用して独自の形状を定義したりできます, 行, または CAD からの DXF インポート.
すべての機能を探索するには SkyCivセクションビルダー セクションのモデリングと分析の容易さを体験してください。, 今日は無料でサインします!
関連リソース


