整形外科材料
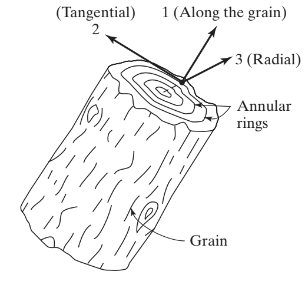
直交異方性プレートの説明を行う前に, 直交異方性材料の例をいくつか見てみましょう. トパーズやバライトの結晶などの材料は直交異方性です (チャンドルパトラ, 2012). もう1つの非常に一般的な直交異方性材料は木材です. 図 1 は、木材の機械的特性が定義されている主軸を示しています.
図 1. 直交異方性材料としての木材 (チャンドルパトラ & ベレガンドゥ ,2012, ページ 233)
軸 1 穀物または繊維に沿って定義されます; 軸 2 接線方向で軸 3 放射状に走る. この例の一般化されたフックの法則 (およびその他の直交異方性材料の場合) 次のように書くことができます
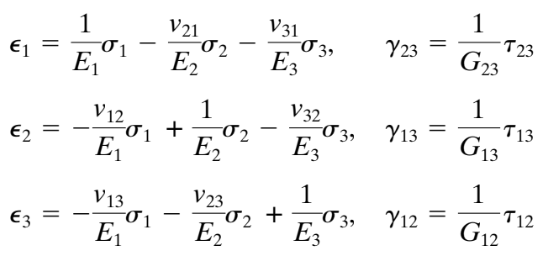
方程式 1. 一般化されたフックの法則 (チャンドルパトラ & ベレガンドゥ,2012, ページ 233)
どこ:
- e1, e2, e3 正常な株です.
- c12, c13, c23 はせん断ひずみです.
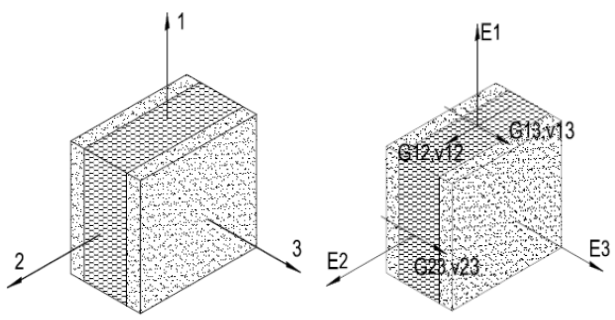
- E1, E2, およびE3 主軸に沿ったヤング率です.
- G12, G13, G23 せん断弾性率です.
- n21, n31, n12, n32, n23 ポアソン比.
- 結合されたインデックスの場合, 最初の数字は応力が加えられる場所を示し、2番目の数字は変形が発生する場所を示します.
したがって, 直交異方性材料の主な違いは、主軸に沿って異なる機械的特性があることです, あれは, “バツ”, “そして”, “と”.
整形外科プレート
いくつかの一般的な使用例があります プレート 構造工学で, 次のように要約できます: 等方性フラット, 複合材またはサンドイッチと補強 (W. Jiang et al, 1997).
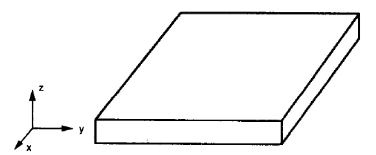
等方性平板は通常の平板です (figure no.2), ポアソン比の値を1つだけ定義する必要があります, 若い, どの方向の機械的特性も変化しないため、せん断弾性率.
Figure no.2. 平板は一般的に等方性です (W. Jiang et al, 1997, ページ 106)
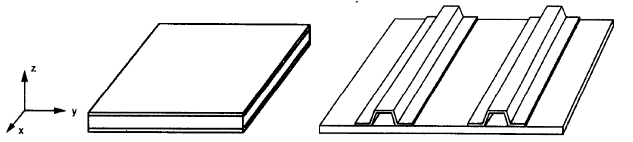
最後の2つのオプションについて, サンドイッチと補強板 (figure no.3), 主軸にさまざまな機械的特性を定義する必要があります. これらの異なる値により、プレートは直交異方性になります.
図 3. 複合 (左) と帽子で補強されたプレート (正しい) (W. Jiang et al, 1997, ページ 106)
直交異方性プレート内, 同じ剛性を持つ2つの軸があります, figure no.3. 軸「x」と「y」は平面上にあります, そして「z」はそれに垂直です.
私たちはそれを言うことができます (W. Jiang et al, 1997):
- Eバツ = Eそして ≠ Eと ; (Eバツ, Eそして )> Eと .
- nxz = nyz ≠nxy ; (nxz, nyz) >nxy
- Gxy = Gxz = Gyz
前に示した式は、「x」および「y」方向の剛性が「z」よりも高いことを意味します。. ポアソン比は、「x」軸と「y」軸によって形成される平面よりも「z」方向に関連する平面でより多くの変形があることも示しています。.
例
説明と設定
過去のセクションで学んだ概念を要約する, SkyCivで例を開発します. これは、ポリスチレンコアで分離された2つのショットクリート層で構築されたサンドイッチ壁/スラブパネルの分析で構成されています. モデリングで使用する機械的特性の次のリファレンスを選択しました: トレス・ビジャビセンシオ他. (2013).

図 4. サンドイッチ壁/スラブパネル
高度なオプションを選択したときにプレートの分析の違いをキャプチャするには (直交異方性), 上記のパネルサンドイッチの簡単な比較と、等方性アプローチを使用した機械的特性の近似を作成します。. 最新のケースでは、主軸に沿って変化しない機械的特性の値を使用しています.
この例の目的は、垂直変位の観点から結果を比較することです。. モデルのセットアップを図に示します。 5.
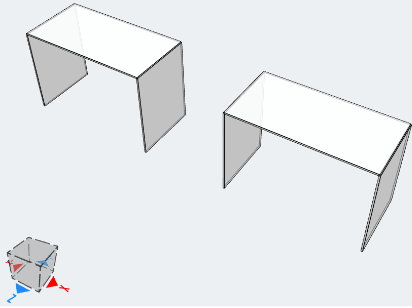 図 5. モデルの設定. 直交異方性 (左), 等方性 (正しい)
図 5. モデルの設定. 直交異方性 (左), 等方性 (正しい)
機械的性質
さまざまな臨床検査レポートに基づく, パネルの直交異方性特性は次のとおりです。 (トレス・ビジャビセンシオ他, 2013):
| 財産 | 値 |
|---|---|
| E1 (MPa) | 5613 |
| E2 (MPa) | 5613 |
| E3 (MPa) | 2807 |
| G12 (MPa) | 2245 |
| G23 (MPa) | 1123 |
| G13 (MPa) | 1123 |
| n12 | 0.2 |
| n23 | 0.25 |
| n13 | 0.25 |
表1. サンドイッチ パネルの直交異方性の機械的特性
Figure no.6. パネル要素の主軸 (トレス・ビジャビセンシオ他, 2013).
等方性の場合の近似値を次の表に示します。.
| 財産 | 値 |
|---|---|
| E (MPa) | 5613 |
| G (MPa) | 2245 |
| n | 0.20 |
表2. サンドイッチ パネルの等方性機械特性の近似
SkyCivでのモデリング
ここで、例をモデル化するために必要な手順を非常に簡潔に説明します。. (プレートモデリングの詳細については, このリンクを参照してください SkyCivプレートモデリング). SkyCivを試したことがない, 構造3Dを使用してフォローする, 単に ここから無料でサインアップ.
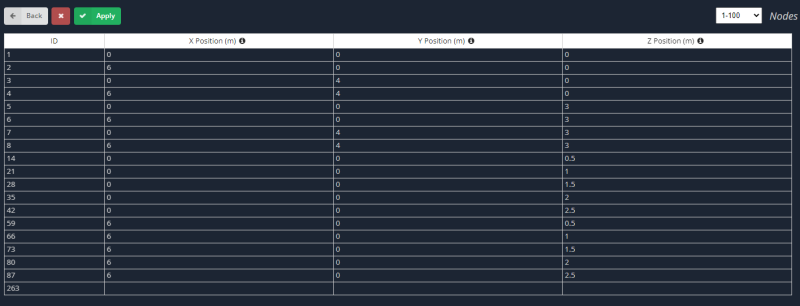
- ノード: 両方のケースを作成するには, まず、水平プレートと垂直プレートに対応するノードを定義します.

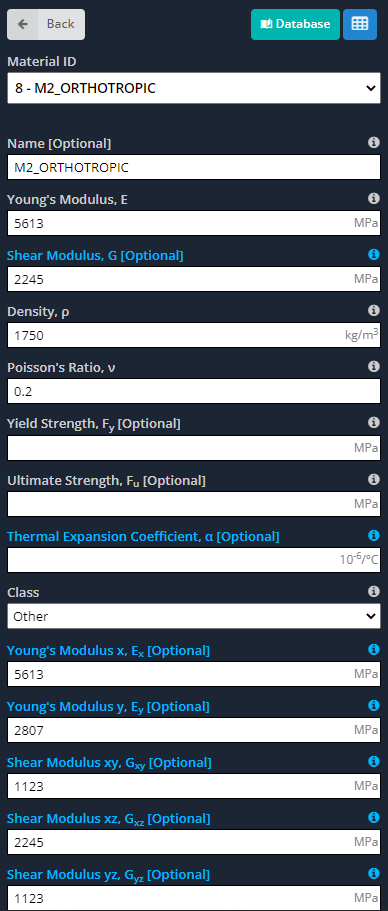
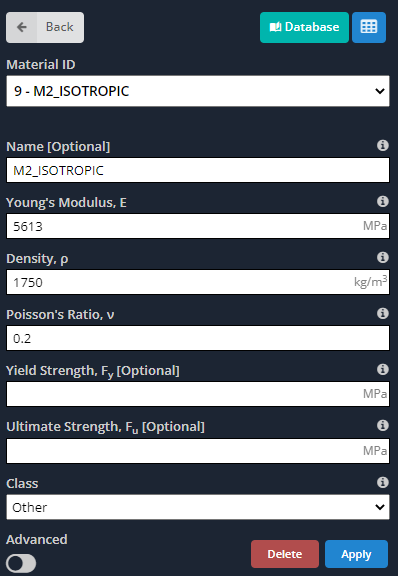
- 材料: 前に言ったように, 直交異方性材料は、主軸に沿って異なる特性を持っています. 次の画像は、モデルに対して定義する必要のある入力を示しています.


- プレート: モデルノードを介して、長方形のプレートを作成します. 垂直壁モデリング用に2つ、床またはスラブ用に1つ.

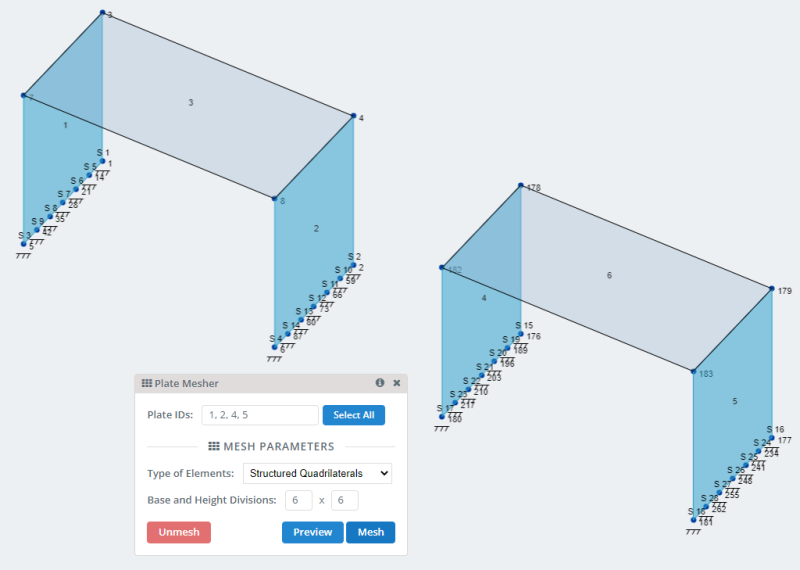
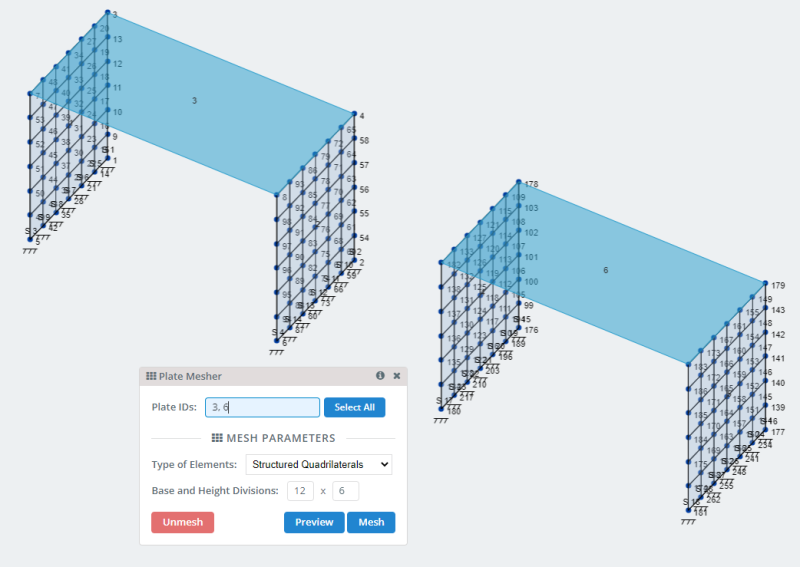
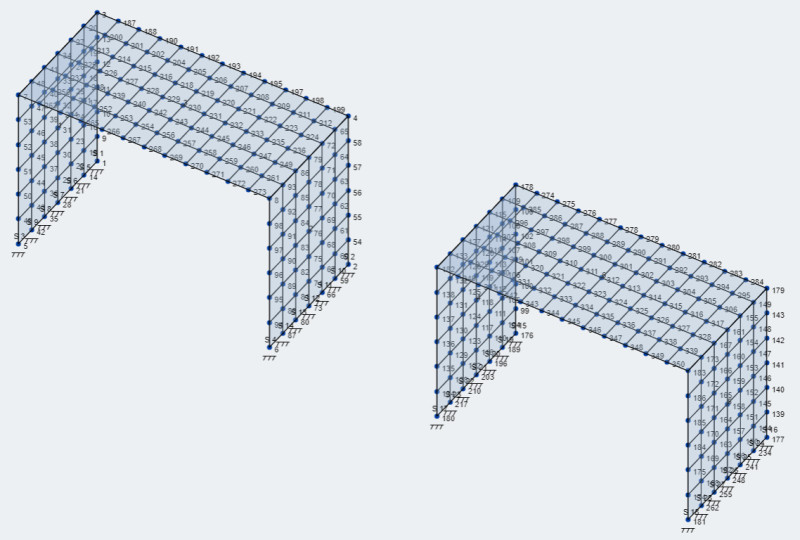
- メッシュプレート: SkyCivには、プレートをメッシュ化するための多くのオプションがあり、 プレートのメッシュ . 私たちのモデルでは、構造化された四角形メッシュのオプションを使用しましょう.



- 自重荷重ケースの定義: プレートの一般的な構造挙動を把握するために、この自重荷重のみを考慮します。.

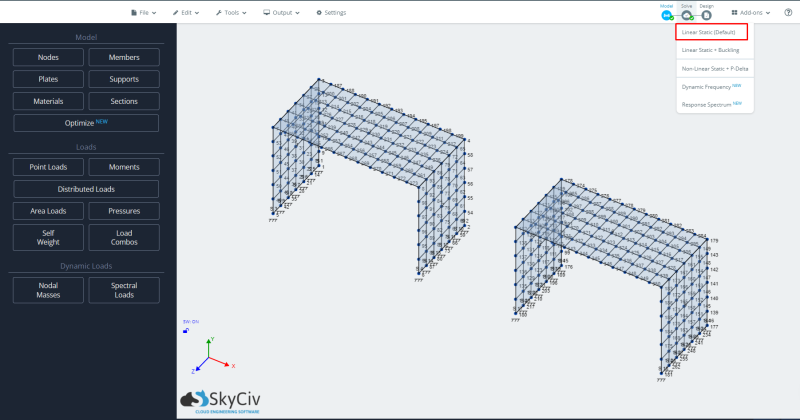
- 分析の実行: モデルを実行するために、線形静的解析のケースを選択します.

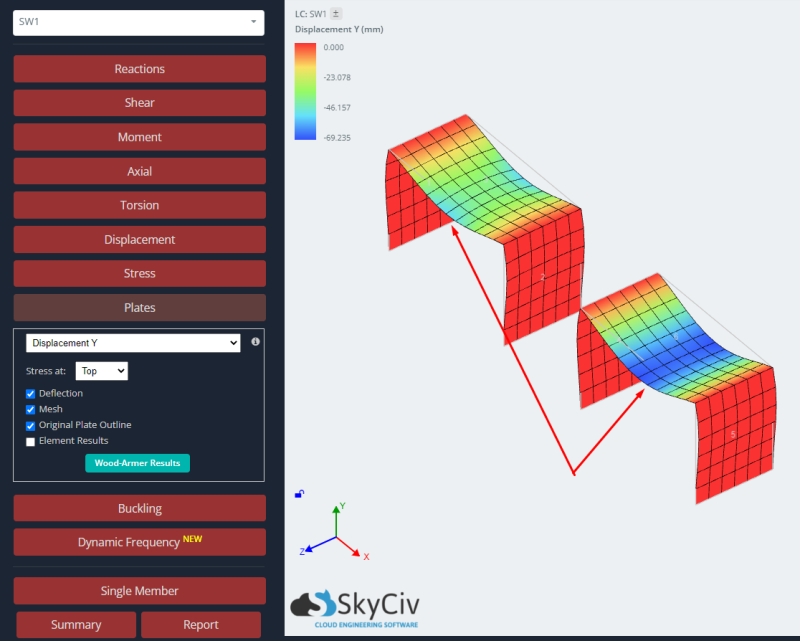
- 結果: 最後に, この時点で、両方のプレートの構造応答を調べます, 等方性および直交異方性の場合. プレート分析の結果の読み取りの詳細については, あなたはこの記事を見ることができます プレート分析結果.

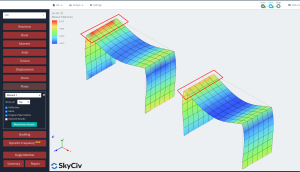
両方のケースの応答を調べる, 垂直変位と曲げモーメントの結果を比較します. 直交異方性のプレートは、等方性の場合よりも小さなたわみと大きな曲げモーメントを示します. 直交異方性アプローチを使用すると、より剛性の高い要素が得られ、これが弾性線形解析のグローバルおよびローカルの結果に影響を与えると言えます。.
無料で始めましょう
チェックアウト SkyCiv構造3D 今すぐ無料でソフトウェアを試してみてください!
参考文献:
- チャンドルパトラ, ティルパティR & ベレガンドゥ, アショク (2012). “工学における有限要素の紹介” 4第3版, ピアソン教育.
- W. 江ら (1997). “補強および非補強直交異方性プレートの有限要素モデリング”, コンピューター & ストラクチャーVol.63, No.1, pp. 105-117, Elsevier Science Ltd.
- トレス・ビジャビセンシオ他 (2013). “モノグラフィック作品: E.P.Sコアを備えた鉄筋コンクリートパネルのEMMEDUEベアリングシステムの設計支援 (発泡スチロールシステム)”. 国立工学大学.
- から取得したすべてのソフトウェアイメージ SkyCiv 構造 3D 解析ソフトウェア