地上設置の完全に機能する例 ASCE を使用したソーラー パネルの風荷重と雪圧の計算 7-16
気候変動の影響を抑えるための再生可能エネルギーの使用における最近の傾向, この問題の解決策として急成長している産業の1つは、太陽エネルギーの使用です。. しかも, ソーラーパネルは、過去数年間で電力が急増しているため、代替エネルギー源として家庭の消費者の間でも人気が高まっています。. 実際に, 住宅の屋根へのソーラーパネルの設置や、地上設置型ソーラーパネルを使用したソーラーファームの建設が増加しています. ソーラーパネルの風荷重と雪圧を計算する必要性は、これらが耐久性を達成するために重要です. 記事上で, ASCEを使用して地上設置型ソーラーパネルの雪と風の負荷を計算する方法について説明します 7-16.
SkyCivは、いくつかのパラメーターを使用して風速計算を自動化します. 私たちを試してみてください ソーラーパネル風荷重計算機
構造データ
この例では, 以下のデータを使用します:
テーブル 1. 風雪荷重計算に必要な建物データ.
| ロケーション | 395 ロッキーポイントロード, コルドバ, メンフィス, テネシー |
| 占有 | 雑多 – ソーラーパネル |
| 地形 | フラット農地 |
| パネル幅 | 16.25 フィート |
| パネルの長さ | 13.33 フィート |
| 取り付け高さ | 8.33 フィート |
| 傾斜角 | 30° |
図 1. 立地 (Googleマップから).
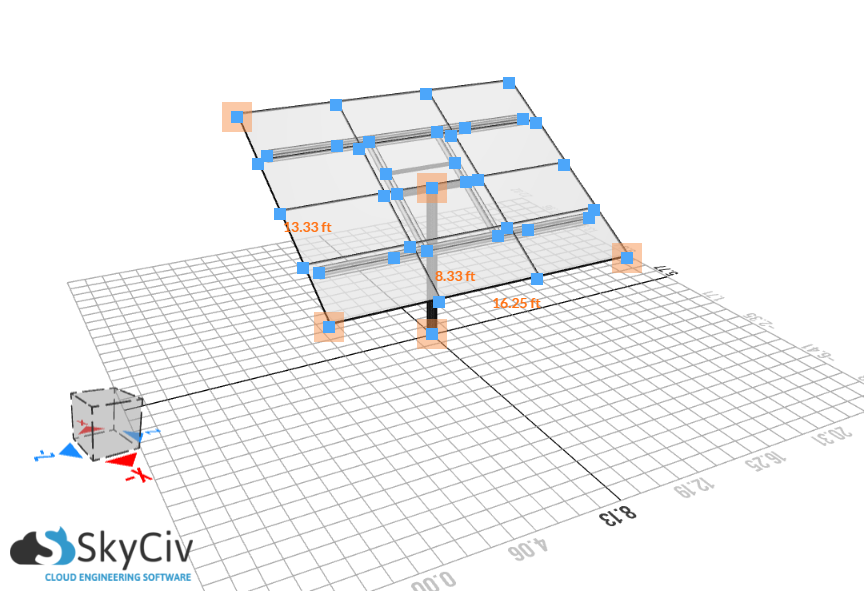
図 2. ソーラーパネルの寸法.
風荷重
ソーラーパネルの風荷重計算では, ASCEを使用します 7-16 章 27 – 風荷重 – ASCEの使用. 傾斜角が 45° 以下の場合、地面に取り付けられたソーラー パネルをモノスロープ屋根の開いた建物と見なし、傾斜角が 45° を超える場合はソリッド サインと見なします。.
設計風圧の決定式は次のとおりです。:
傾斜角 ≤ 45° の場合 (モノスロープ屋根の開放的な建物とみなされる):
\(p = {q}_{h}G{C}_{N}\) (1)
傾斜角用 > 45° (ソリッド サインと見なされる):
\(p = {q}_{h}G{C}_{f}\) (2)
どこ:
\(G\) =突風効果係数
\({C}_{N}\) = 開いたモノスロープ屋根の正味の力係数
\({C}_{f}\) = ソリッド サインの正味の力係数
\({q}_{h}\) = 基準高度での速度圧力, \(h\), PSFで, 式で与えられる:
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\) (3)
\({K}_{z}\) =速度圧力係数
\({K}_{zt}\)=地形的要因
\({K}_{d}\) =風向性係数
\({K}_{e}\) = 地面の標高係数
\(V \) = mphでの基本的な風速
傾斜角度に注意 > 45°, 使用する寸法はソーラー パネルの垂直投影であり、ソリッド サインの正味の力係数の式を使用します。. 以下の各パラメータの詳細を詳しく説明します.
リスクカテゴリー
最初のステップは、使用または占有率に基づいて、ソーラー パネルのリスク カテゴリを決定することです。. テーブルから 1.5-1 ASCEの 7-16, この例の地上設置型ソーラー パネルは、リスク カテゴリ I に分類できます。.
基本風速, \(V\)
ASCE 7-16 位置の対応する基本的な風速を図26.5-1Aから1Cから取得できる風マップを提供します. 図26.5-1Aより, コルドバ, メンフィス, テネシーは図の赤い点のどこかに近い 3 未満, そしてそこから, 基本的な風速, \(V\), です 100 mph. 基本的な風速値は、最も近い風速コンターから補間されることに注意してください.
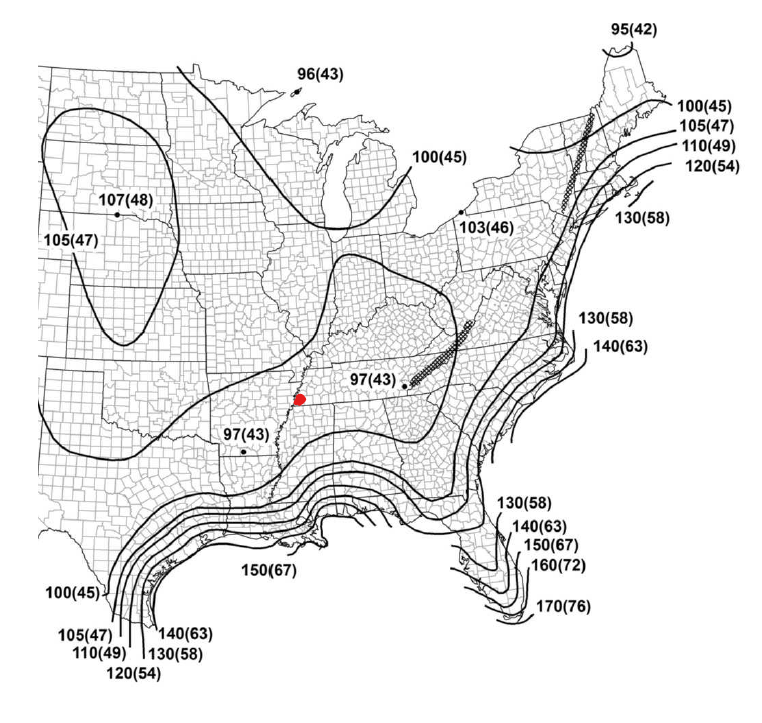
図 3. ASCE 図 26.5-1A の基本風速マップ 7-16 (リスク カテゴリ I) ソーラーパネルの位置を示す赤い点.
SkyCivは、いくつかのパラメーターを使用して風速計算を自動化します. 私たちを試してみてください ソーラーパネル風荷重計算機
ばく露カテゴリー
分析する風向に応じて, ソーラー パネルの露出カテゴリは、セクションに基づいて風上 45° セクターから決定されるものとします。 26.7 ASCEの 7-16. しかも, セクション C26.7 は、露出 B の例を示す航空写真を提供します。, C, および図 C26.7-5 ~ C26.7-7 の D.
この例では, 南方向からの風のみを使用します. したがって, 航空写真の例に基づいて, 図 C26.7-6 に基づいて、風上地形を露出 C に分類できます。(b) または “障害物が点在する開けた地形で、高さが一般的に 30 フィート (9.1 メートル)” 図に示すように 4 未満. 速度圧力係数を計算する際に露出カテゴリを使用します \({K}_{z}\)スパン> および/または地形的要因 \({K}_{zt}\) 必要に応じて.
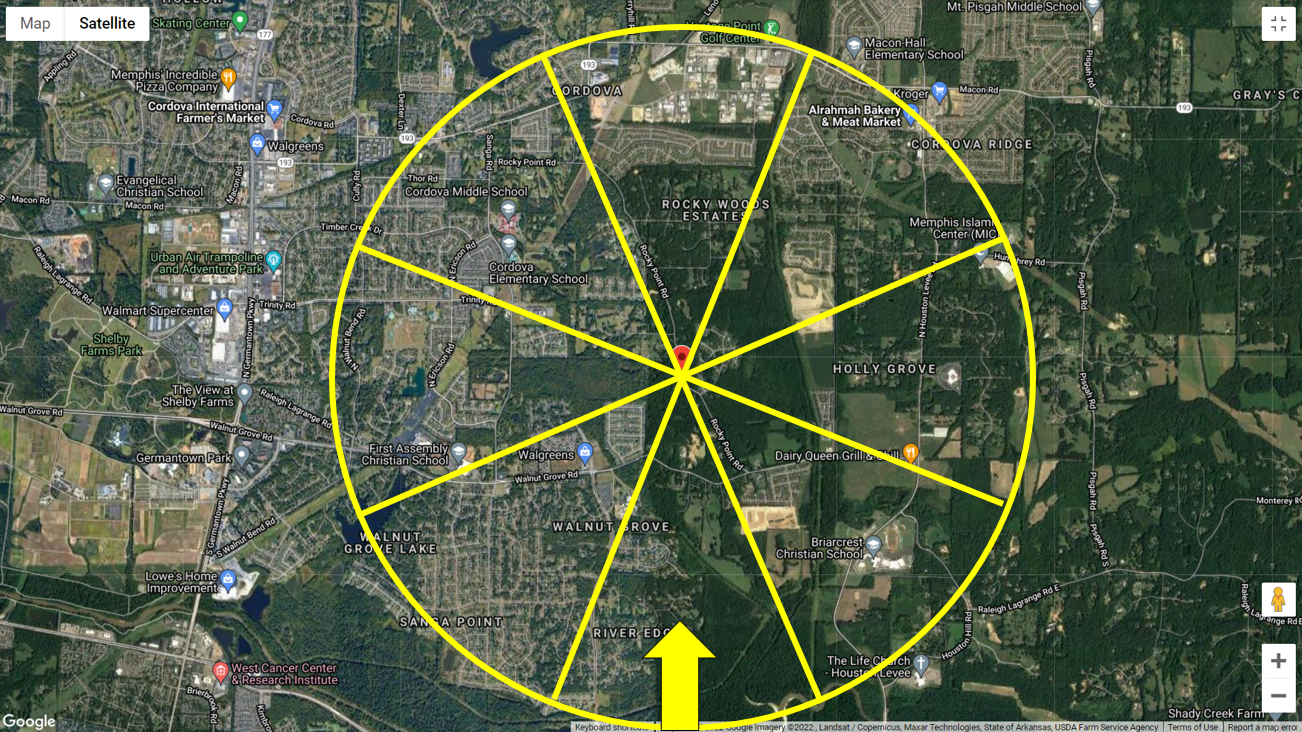
図 4. 南からの風が吹く地形の航空写真.
風向係数, \( {K}_{d} \)
風向係数, \({K}_{d} \), ソーラーパネルの場合は次のようになります 0.85 ソーラー パネルは MWFRS と見なすことができるため、 (オープンモノスロープ) 傾斜角度が 45° 以下の場合、傾斜角度が 45° を超える場合は表に基づいてベタ サインとして 26.6-1 ASCEの 7-16.
地面の標高係数, \( {K}_{e} \)
地面の標高係数, \({K}_{e} \), テーブルを使用して計算できます 26.9-1 ASCEの 7-16. この例では, サイトの標高が等しいため 350.48 フィート, \({K}_{e} \) 式を使用して計算できます:
\( {K}_{e} = {e}^{-0.0000362{z}_{g}} \) (4)
\( {K}_{e} = {e}^{-0.0000362(350.48)} = 0.987\)
\( {K}_{e} = 0.987 \)
方程式の使用 (4), \({K}_{e} \) に等しい 0.987.
地形的要因, \( {K}_{zt} \)
地形係数を計算するためのパラメータ, \({K}_{zt}\), 詳細は図 26.8-1 ASCEの 7-16. 地形係数をさらに計算する必要があるかどうかを判断するには, セクションを使用して確認する必要があります 26.8.1. サイトが記載されているすべての条件を満たしていない場合, 次に、地形係数は 1.0. Google標高から生成された地表標高から, 地形は平坦であると仮定できます, したがって, \({K}_{zt}\) と仮定することができます 1.0 南からの風に.
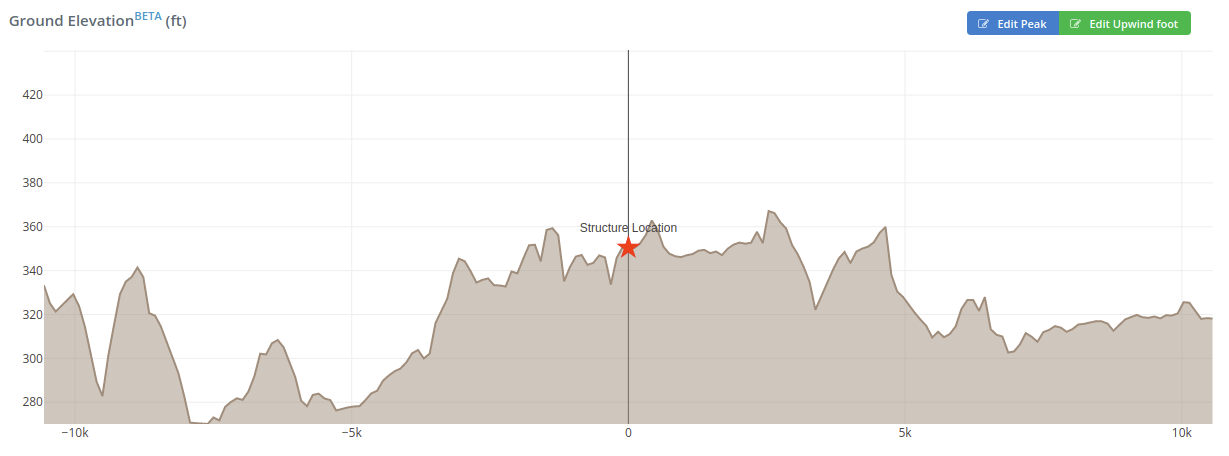
図 5. 南北風向におけるサイトの標高プロファイル.
速度圧力係数, \({K}_{z}\)
速度圧力係数, \({K}_{z}\), テーブルを使用して計算できます 26.10-1 ASCEの 7-16. このパラメータは、風圧が考慮されるポイントの地上高さによって異なります, および露出カテゴリ. しかも, 表に示されている値は、次の式に基づいています:
15フィートの場合 < \({z}\) < \({z}_{g}\): \({K}_{z} = 2.01(z/{z}_{g})^{2/α}\) (5)
ために \({と}\) < 15フィート: \({K}_{z} = 2.01(15/{z}_{g})^{2/α}\) (6)
どこ:
テーブル 3. α の値と \({z}_{g}\) テーブルから 26.11-1 ASCEの 7-16.
| 曝露 | a | \({z}_{g}\) (フィート) |
|---|---|---|
| B | 7 | 1200 |
| C | 9.5 | 900 |
| D | 11.5 | 700 |
この例では, ソーラーマウントの高さの標高を考慮します.
\({K}_{z} = 2.01((15)/(900))^{2/(9.5)} = 0.85 \)
\({K}_{z} = 0.85 \)
速度圧力
方程式から (3), 速度圧力を解くことができます, \( {q}_{h}\) PSFで, に等しい取り付け高さで 8.33 フィート.
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\)
\({q}_{h} = 0.00256(0.85)(1.0)(0.85)(0.987)(100)^2 = 18.256 psf\)
\({q}_{h} = 18.256 psf\)
設計風圧を計算するには, 方程式を使用します (1). これらのパラメータの詳細を以下に示します.
突風効果係数, \(G\)
ガスト効果係数の決定, \(G\), まず、構造の基本固有振動数を計算する必要があります \( {n}_{1} \). もし \( {n}_{1} \) よりも少ない 1 Hz, フレキシブル構造に分類されます, したがって、計算する必要があります \(G\) セクションの使用 26.11.5. この例では, 単純化されたアプローチ, ソーラーパネルは剛体であると仮定します, どこ \(G\) に等しい 0.85 セクションに基づく 26.11.1 ASCEの 7-16. 特に柔軟な構造の場合、突風効果係数を決定する際には、構造の基本固有振動数をチェックするための十分な注意が必要であることに注意してください。これは、このパラメータを拡大するためです.
正味圧力係数, \({C}_{N}\), 傾斜角 ≤ 45°
正味圧力係数を決定するには, \( {C}_{N} \), 太陽光パネルはモノスロープ屋根の開放的な建物と仮定します. これらの値は図から取得できます 27.3-4 ASCEの 7-16 の仮定で “クリアウィンドフロー。” これらの値は、傾斜角が 45° 以下のソーラー パネルにのみ適用されることに注意してください。
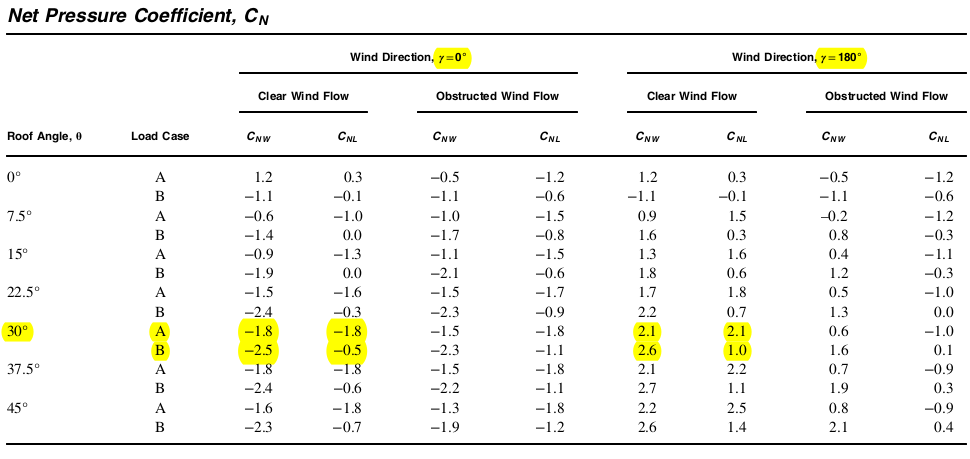
図 6. 正味圧力係数, \( {C}_{N} \), 図の値 27.3-4 ASCEの 7-16 モノスロープ屋根の開放的な建物用.
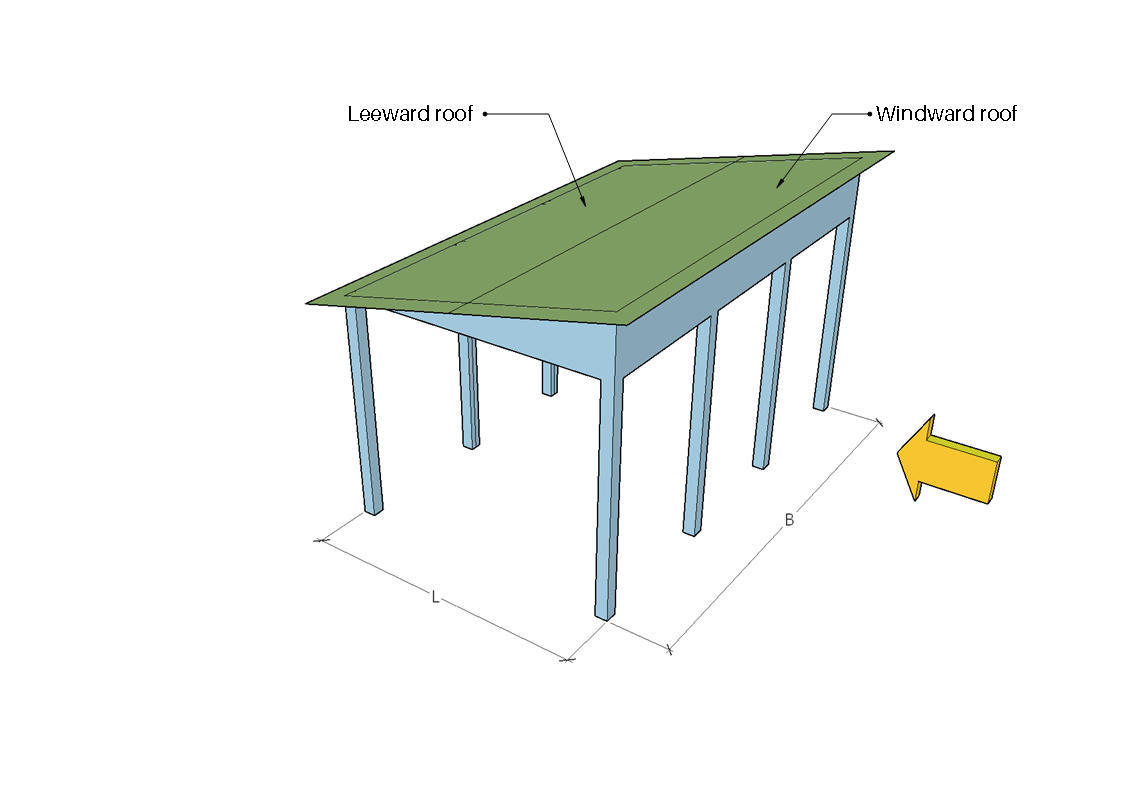
図 7. 方向角が 0° の場合の風上および風下ゾーン .
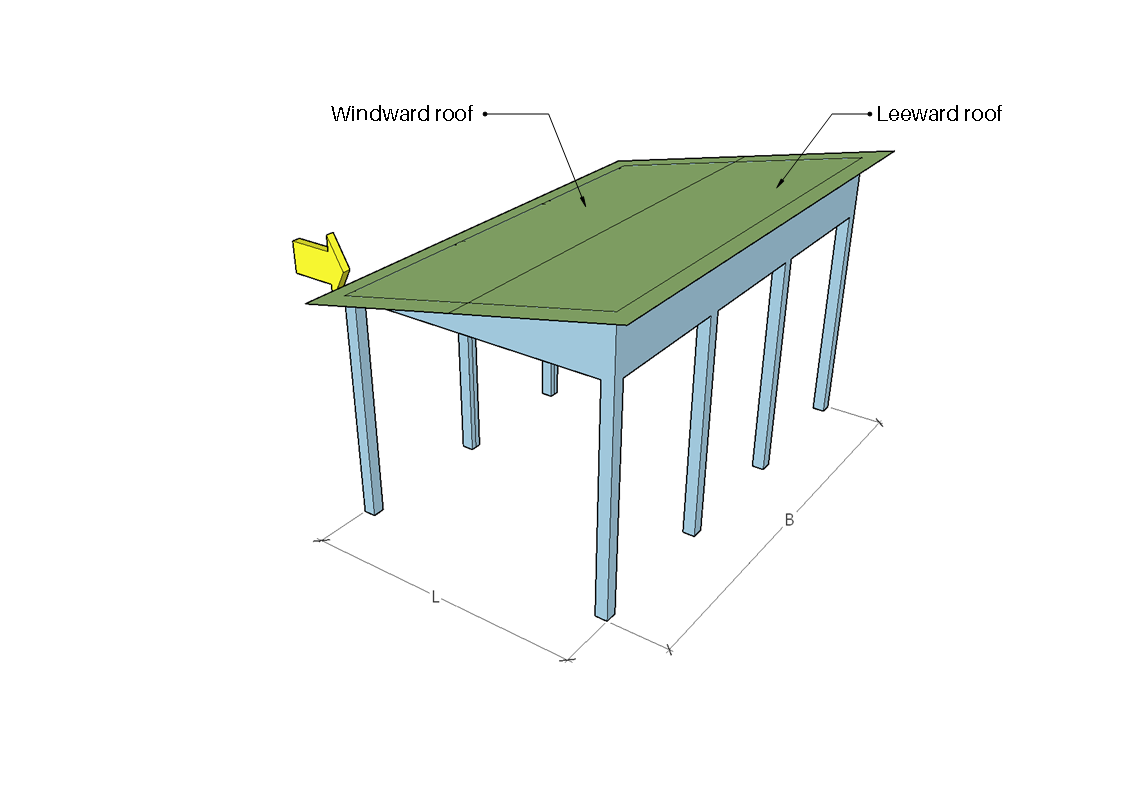
図 8. 180°に等しい方向角の風上および風下ゾーン.
ソーラーパネルの傾斜角は30°なので, 対応する正味圧力係数, \( {C}_{N} \), 使用するものは次のとおりです:
テーブル 4. の値 \( {C}_{N} \) 図に基づいて使用する 27.3-4 ASCEの 7-16.
| 荷重ケース | 方向 = 0° | 方向 = 180° | ||
|---|---|---|---|---|
| \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | |
| あ | -1.8 | -1.8 | 2.1 | 2.1 |
| B | -2.5 | -0.5 | 2.6 | 1.0 |
負の値は風圧が地表から離れて作用していることを意味し、正の値は地表に向かって作用している風圧を表すことに注意してください。. テーブルから 4, 4つを考慮すると推測できます (4) 太陽光パネルの風荷重の荷重ケース.
設計風圧 – 傾斜角 ≤ 45°
傾斜角のあるソーラーパネルの風荷重を計算する場合 > 45°, 方程式を使用します (1), したがって, 地上に設置されたソーラーパネルにかかる風荷重:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
テーブル 5. 構造物に適用される、地上に取り付けられたソーラー パネルの計算された風荷重.
| 荷重ケース | 方向 = 0° | 方向 = 180° | ||
|---|---|---|---|---|
| 風上, psf |
風下, psf | 風上, psf | 風下, psf | |
| あ | -27.932 | -27.932 | 32.587 | 32.587 |
| B | -38.794 | -7.759 | 40.346 | 15.518 |
したがって, 適用時の地上設置型ソーラー パネルの風荷重は次のとおりです。:
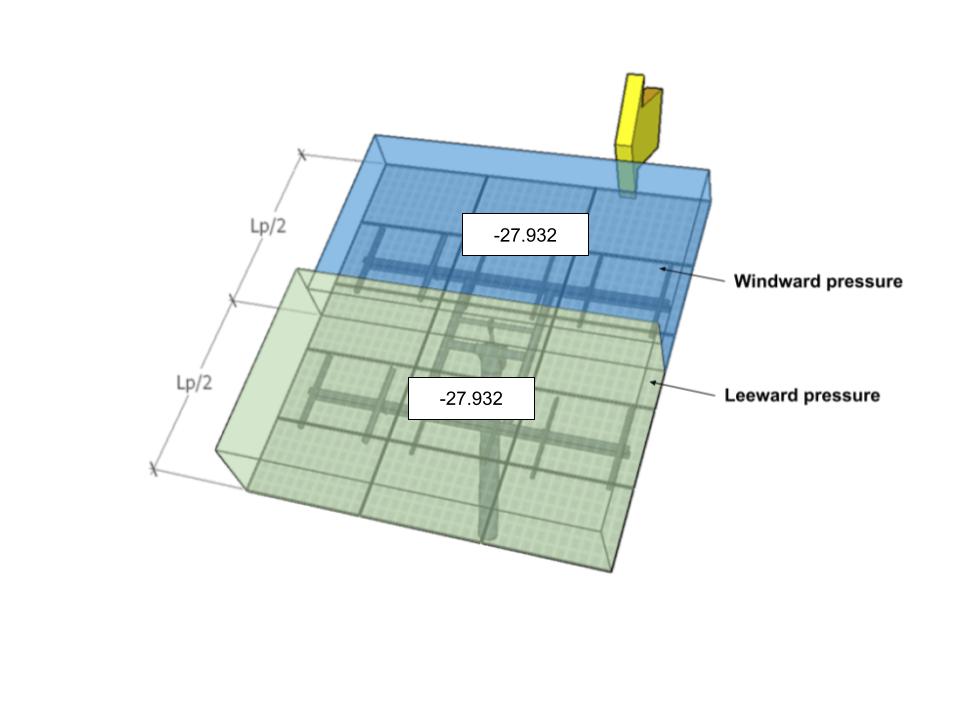
図 9. 方位角0°の設計風圧 – 荷重ケース A.
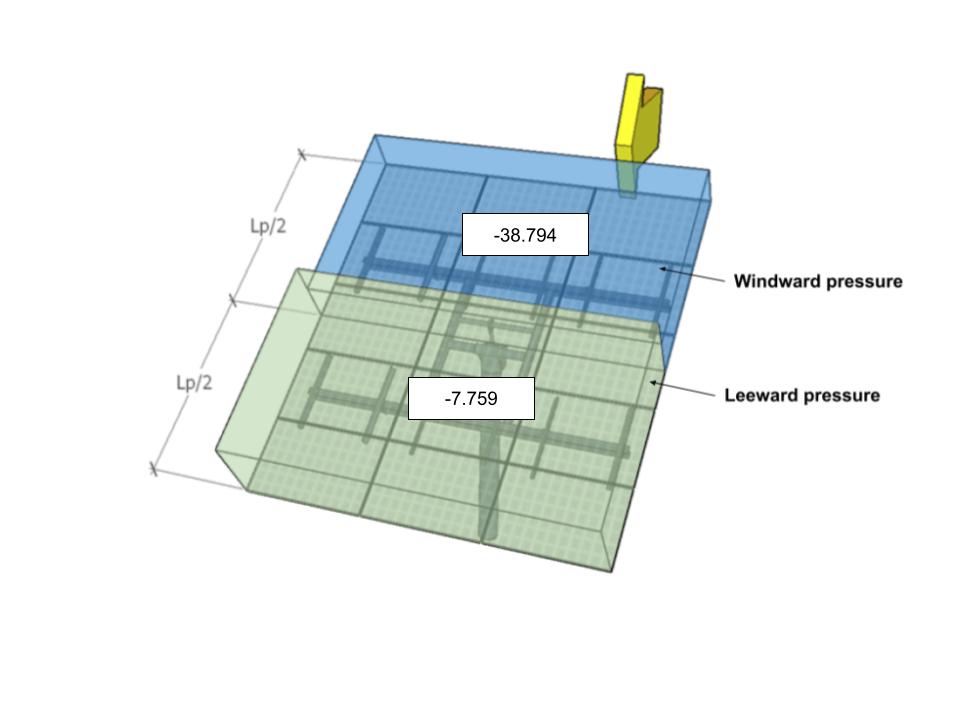
図 10. 方位角0°の設計風圧 – 荷重ケース B.
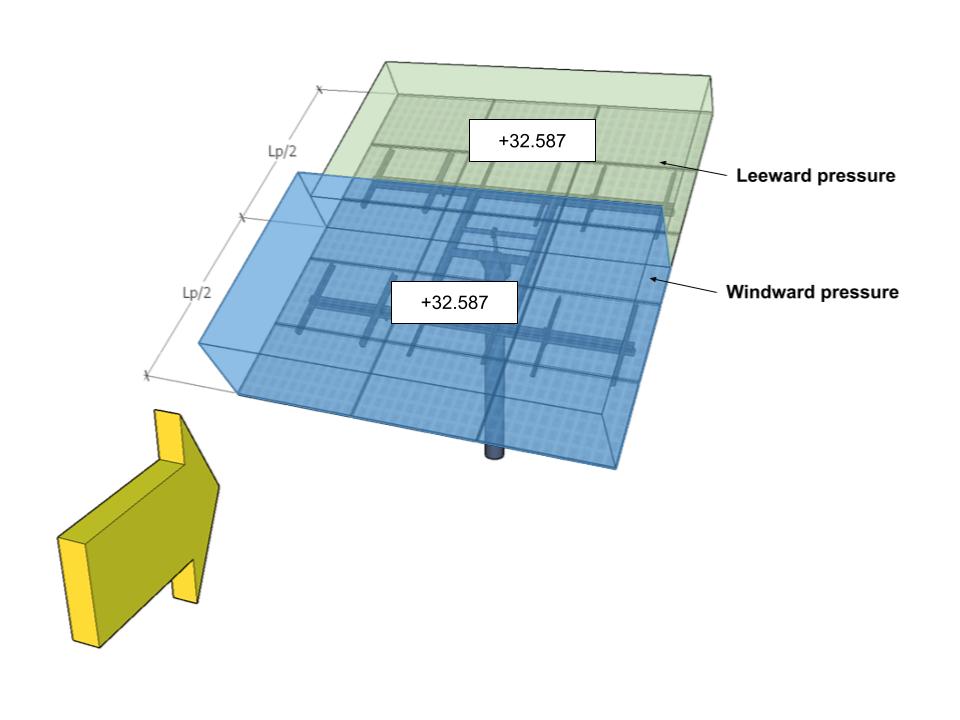
図 11. 方位角180°の設計風圧 – 荷重ケース A.
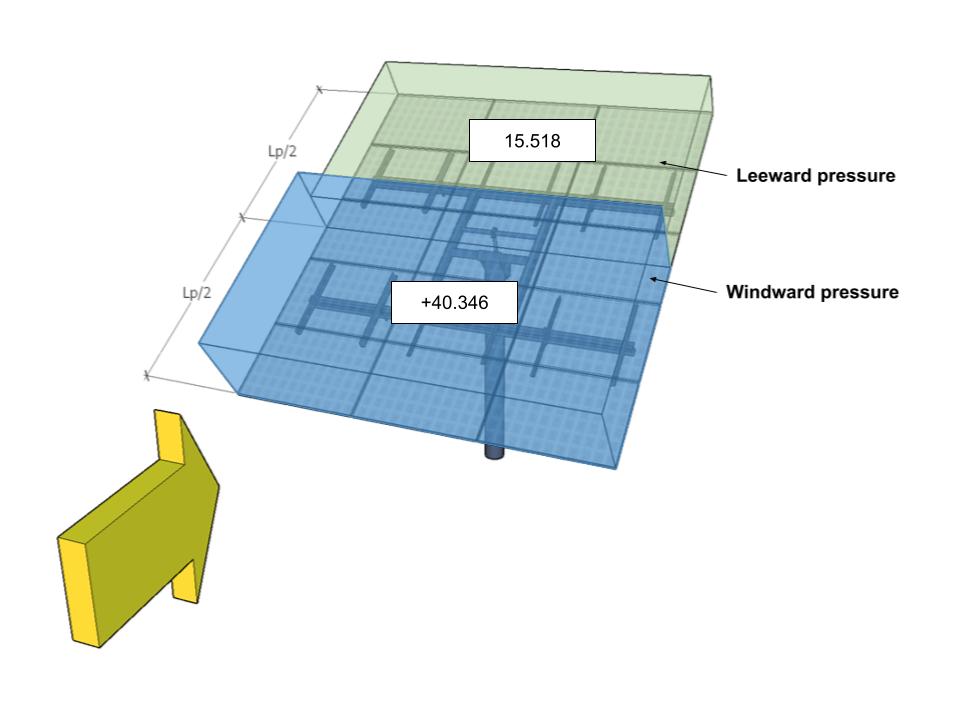
図 12. 方位角180°の設計風圧 – 荷重ケース B.
正味の力係数, \({C}_{f}\), – 傾斜角 > 45°
ソーラー パネルの傾斜角が次のように変更されたとします。 60°. ソーラー パネルの垂直射影を使用し、この射影の頂点まで計算された速度圧力を備えたソリッド サインと見なす必要があります。.
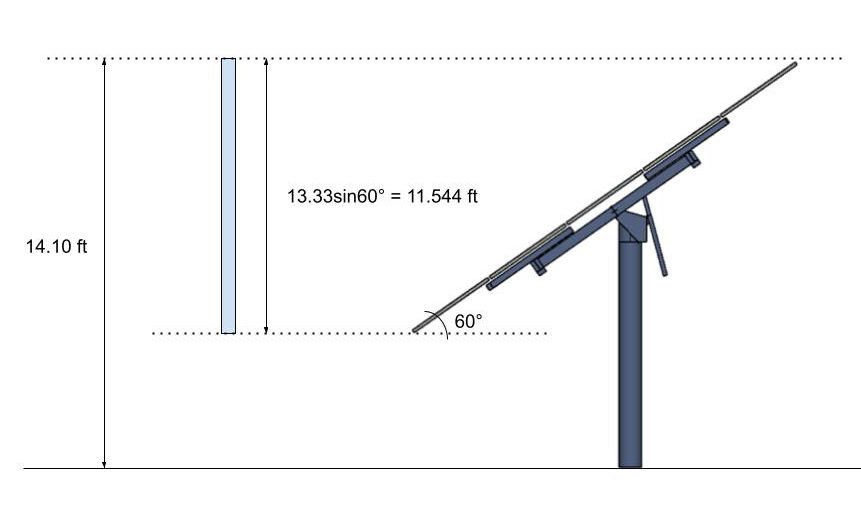
図 13. ソリッドサインと見なされるソーラーパネルの垂直投影.
地面からプロジェクトの上部までの高さはまだ 15 フィート, 計算されたものを引き続き使用できます \( {K}_{z}\) 上. したがって, の計算値 \( {q}_{h}\) まだ同じだろう. 係数の正味, \( {C}_{f}\), 使用するために図から得ることができます 29.3-1 ASCEの 7-16. しかも, これらの力係数を計算する際に, 単純化されたアプローチのケース A のみを検討します. 図から 29.3-1:
\({q}_{h} = 18.256 psf\)
\( B = 16.25 ft\)
\( s = 11.544 ft\)
\( h = 14.102 ft\)
\( s/h = 0.818\)
\( B/s = 1.408\)
の集計値から \( {C}_{f} \) 図中 29.3-1, の既知の値を補間します \( B/s \) に等しい 1 そして 2, そして \( s/h \) に等しい 0.9 そして 0.7.
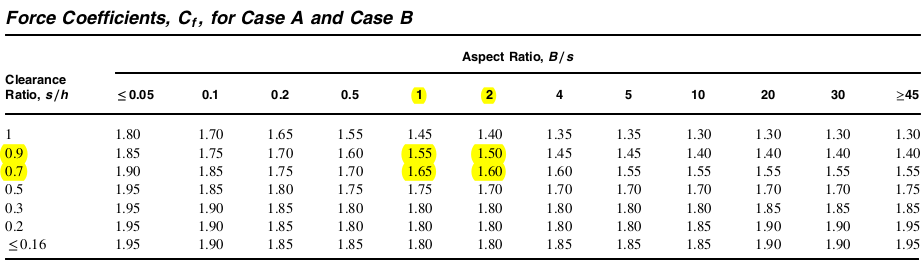
図 14. 正味の力係数, \( {C}_{f} \), 図の値 29.3-1 ASCEの 7-16 立体標識用.
強調表示された値を補間して取得する \( {C}_{f} \) 私たちから \( B/s \) そして \( s/h \), 我々が得る:
\( {C}_{f} = 1.5706 \)
設計風圧 – 傾斜角 > 45°
傾斜角のあるソーラーパネルの風荷重を計算する場合 > 45°, 方程式を使用します (2), したがって, 地上に設置されたソーラーパネルにかかる風荷重:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
\( {C}_{f} = 1.5706 \)
\(p = {q}_{h}G{C}_{f} = (18.256)(0.85)(1.5706) = 24.372 psf\)
\(p = 24.372 psf\)
したがって, 適用された場合、地上に取り付けられたソーラーパネルにかかる風荷重: 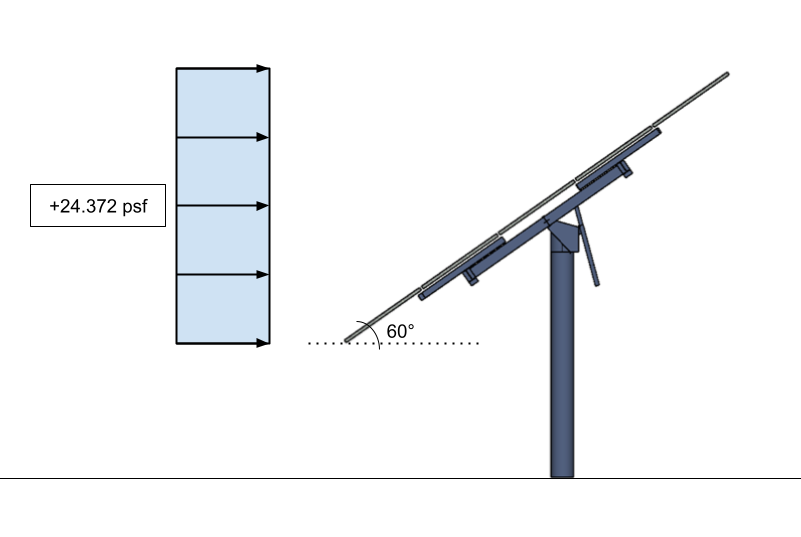
図 15. ソーラーパネルの設計風圧を実印で表示 – 垂直投影に適用.
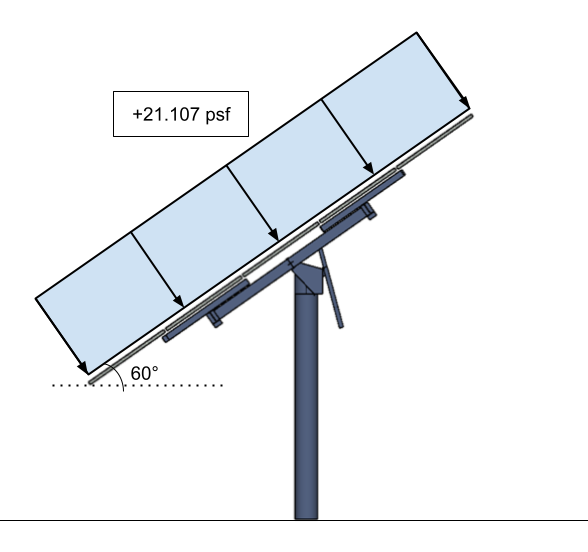
図 16. ソーラーパネルの設計風圧をベタで換算したもの – ソーラーパネルの表面に塗布.
風の計算はすべて、SkyCiv Load Generator for ASCE を使用して実行できます 7-16 (ソーラーパネル風荷重計算機). ユーザーはサイトの場所を入力して、風速と地形データを取得できます, ソーラー パネルのパラメータを入力し、設計風圧を生成します. スタンドアローン版で, このプロセスを合理化し、ソーラー パネルの詳細な風荷重計算レポートを取得できます。!
スノーロード
雪が降る地域向け, ソーラーパネルの積雪量も考慮する必要があります. ソーラーパネルの積雪量を計算するには, 章を使用します 7 ASCEの 7-16. 太陽光パネルの構造をモノスロープ屋根の建物と考え、 バランスの取れた積雪量のみを考慮します (傾斜屋根積雪荷重). 当社のソーラーパネルの積雪量を求める式は次のとおりです。:
平屋根の積雪荷重を計算するには \({p}_{f} \):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \) (7)
どこ:
\({C}_{e} \) = 露出係数
\({C}_{t} \) = 熱係数
\({I}_{s} \) = 積雪荷重の重要度
\({p}_{g} \) =積雪荷重, PSFで
傾斜屋根の積雪荷重を計算するには \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \) (8)
どこ:
\({C}_{s} \) = 屋根勾配係数
\({p}_{r} \) = 雨雪追加料金の負荷
ばく露係数, \({C}_{e} \)
露出係数, \({C}_{e} \), 表から決定できます 7.3-1 ASCEの 7-16 屋根の表面粗さと露出に基づく. Google マップから取得した場所の衛星画像から, 場所が 表面粗さC (障害物が点在する開けた地形で、高さが一般的に 30 フィート) ソーラーパネルが 完全に露出し、障害物がない. したがって, の ばく露係数, \({C}_{e} \), 構造体の 0.9.
熱係数, \({C}_{t} \)
熱的要因, \({C}_{t} \), 表から決定できます 7.3-2 ASCEの 7-16 冬季の構造物の熱条件に基づく. テーブルから, ソーラーパネルを次のように分類できます “加熱されていないオープンエア構造。” したがって, の対応する 熱係数, \({C}_{t} \), は、構造が等しいためです 1.2.
積雪荷重の重要度係数, \({I}_{s} \)
積雪荷重の重要係数, \({I}_{s} \), 表から決定できます 1.5-2 ASCEの 7-16 構造のリスクカテゴリに基づく. 構造物はリスク区分Ⅰに分類されているため, テーブルから, \({I}_{s} \) に等しい 0.8.
地面雪荷重, \({p}_{g} \)
地雪荷重, \({p}_{g} \), 図から決定できます 7.2-1 ASCEの 7-16 以下に示すように. この図から, の 地上積雪量, \({p}_{g} \) 私たちのソーラーパネルは 10 psf.
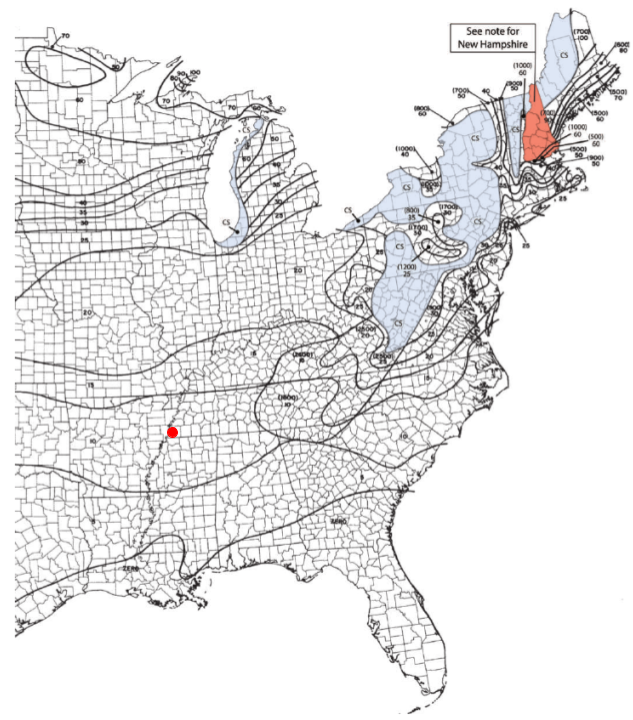
図 17. 図より地上積雪量マップ 7.2-1 ASCEの 7-16 ソーラーパネルの位置を示す赤い点.
SkyCiv はまた、いくつかのパラメーターを使用して地上積雪量の計算を自動化します. 私たちを試してみてください ソーラーパネル風荷重計算機
陸屋根積雪荷重, \({p}_{f} \)
上記のパラメータから, 平屋根の積雪荷重はすでに計算できます, \({p}_{f} \), 式を使用する (7):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \)
\({p}_{f} = 0.7(0.9)(1.2)(0.8)(10) = 6.048 psf \)
\({p}_{f} = 6.048 psf \)
屋根の勾配係数, \({C}_{s} \)
屋根の勾配係数は、次の図から計算できます。 7.4-1 ASCEの 7-16 傾斜角度によって, 屋根面の下の障害物, および熱係数の値 \({C}_{t} \). 私たちのソーラーパネルには, 私たちのソーラーパネルは次のように分類されると仮定します “滑りやすい表面。” 熱的要因から \({C}_{t} \) に等しい 1.2, の値をすでに補間することができます \({C}_{s} \) 7-2cから. グラフから, 既知の値は:
\({C}_{s} = 1.0 \) for 15°
\({C}_{s} = 0.0 \) for 70°
得られるこれらの値を補間する:
\({C}_{s} = 0.727 \) for 30°
したがって, \({C}_{s} = 0.727 \) 私たちのソーラーパネルに.
雨雪割増料金, \({p}_{r} \)
追加の 5 psf レイン オン スノー サーチャージ ロード, \({p}_{r} \), 場所について考慮する必要があります。 \({p}_{g} \) 以下です 20 psf しかしゼロではない, 傾斜角のあるすべての屋根用 (度単位) 未満 \( W/50 \) 度 \( W \) 軒から棟までの水平距離. の値 \({p}_{r} \) 傾斜屋根にのみ適用されます (バランスの取れた) 荷重ケース. この例では:
\(W = 13.33 cos 30° = 11.544 ft \)
\( W/50 =0.231° \)
以来 \({p}_{g} = 10 psf \) ただし、傾斜角 30° はより大きい \( W/50 =0.231° \), \({p}_{r} \) は無視でき、次の値に等しい 0.0
勾配屋根積雪荷重, \({p}_{s} \)
方程式から (8), 傾斜屋根の積雪荷重を計算できます \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \)
\({p}_{s} = (0.727)(6.048) + 0.0 = 4.397 psf \)
\({p}_{s} = 4.397 psf \)
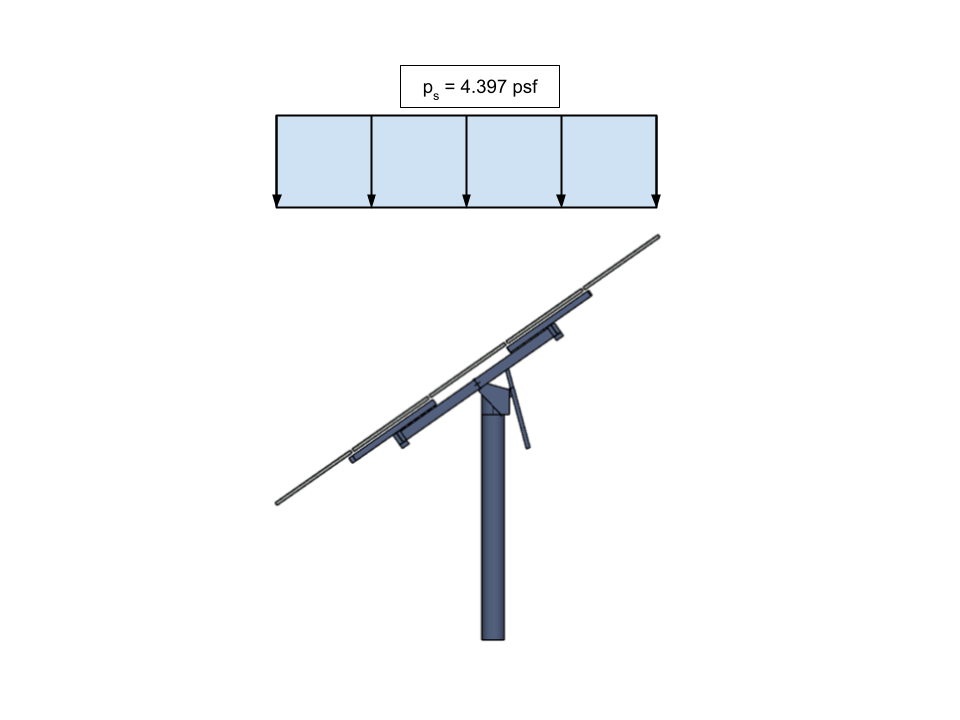
図 18. 計算された平衡積雪量 (傾斜屋根積雪荷重) 構造物の水平投影に適用されるソーラーパネル用.
=建物またはその他の構造物の場所での地面からの高さ \({p}_{s} \) 構造の水平投影に適用されます. モデルに適用できるように、この値を同等の傾斜圧力荷重に変換する必要があります。.
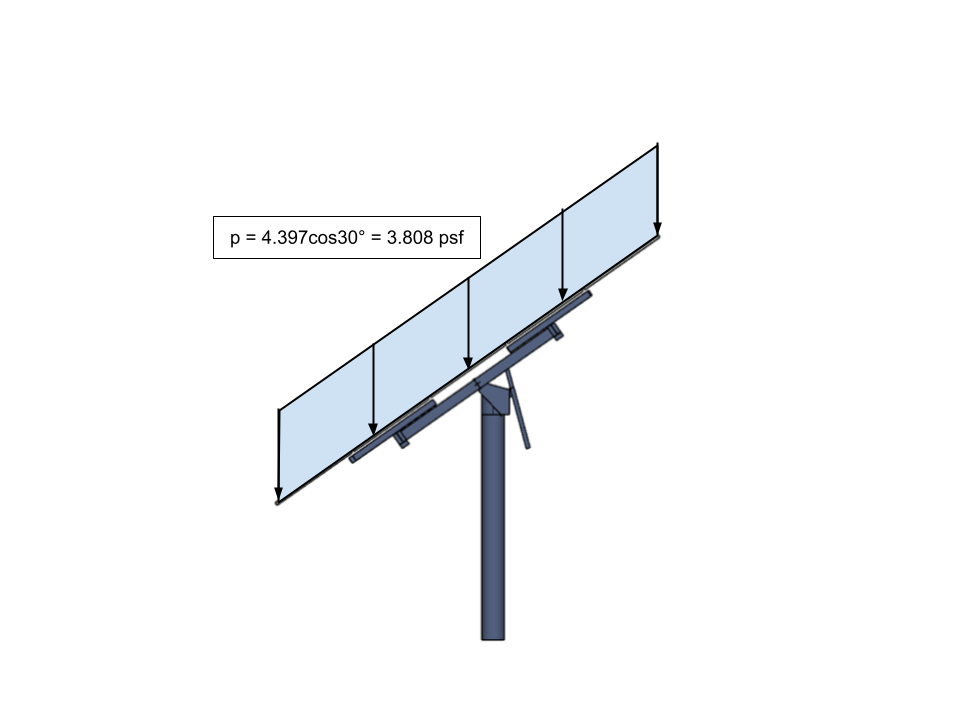
図 19. 換算平衡積雪量 (傾斜屋根積雪荷重) ソーラーパネルをモデルに適用するため.
積雪量の計算は、SkyCiv Load Generator for ASCE でも実行できます 7-16. しかしながら, スタンドアロン バージョンとプロフェッショナル アカウントでのみ利用可能です。.
SkyCiv Load Generator
地上高として, 数回クリックして入力するだけで、地上に取り付けられたソーラーパネルの風荷重と雪荷重を取得できます. スタンドアロン版を購入するか、Professional アカウントにサインアップする場合, ソーラー パネル プロジェクトの詳細な風と雪の計算レポートを生成できます。!
これらのリンクから、ソーラー パネルの詳細な風と雪の負荷レポートを確認できます。:
さらに, また、SkyCiv Load Generator API を使用して独自のソーラー パネル風荷重計算機を作成することもできます。. わずかな入力で, ソーラーパネルシステムを自動的に設計します. こちらからAPIドキュメントを確認できます リンク.
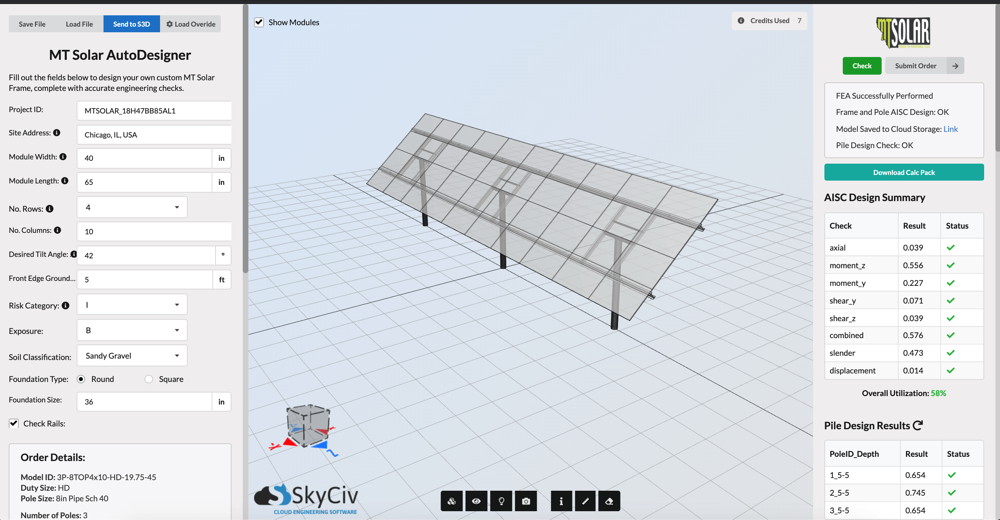
図 20. SkyCiv APIを使用してMTソーラー用に作成されたソーラーパネルのカスタムソリューション.
追加のリソースについて, これらのリンクを使用できます:
- SkyCiv Load Generatorの概要
- ASCE 7-16 風荷重の計算 (ソーラーパネル)
- ASCE 7 積雪荷重の計算
- ASCEで屋根の雪のドリフト荷重を計算して適用する方法 7-10
- ASCEを使用した屋根雪荷重の計算 7-10
構造エンジニア, 製品開発
MS土木工学
参考文献:
- コールボーン, W. L。, & スタッフォード, T. E. (2020, 4月). 風荷重: ASCEの風荷重規定へのガイド 7-16. アメリカ土木学会.
- アメリカ土木学会. (2017, 六月). 建物やその他の構造物の最小設計荷重と関連基準. アメリカ土木学会.
- の計算を説明するために
- MTソーラー



