Structural 3Dで構造の固有振動数を計算します
動的周波数分析, または モーダル分析, 固有振動数を決定するために必要です (または共振周波数) 最大応答を予測するための構造の解析. 構造物に加わる振動荷重が固有振動数と一致する場合, システムの破壊につながる危険な場合があります.
入力
ユーザーは節点質量を簡単に追加できます, 既存の静的荷重を節点質量に変換するだけ. SkyCiv Structural 3Dは自動的に節点質量を計算します (ロードグループに基づく) そしてそれらを構造に適用します, モデルの動的周波数効果を分析できるように. 始めること, クリック 節質量 左メニューから. ユーザーは、既存の荷重から節点質量を変換できます. これは、ユーザーがクリックしたときの例です 荷重の変換 下 節質量 入力:
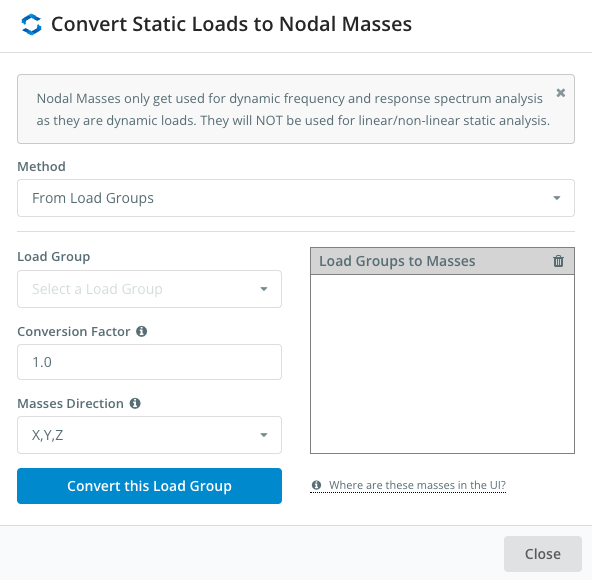
これにより、ユーザーは荷重グループを追加してモーダルマスに変換できます。, 含まれる負荷の完全な制御をユーザーに与える, 質量の方向と因子のコントロール付き.
ユーザーは、Xを入力して、任意のノードで独自の節点質量を指定することもできます。,そして,Z並進および回転質量値:
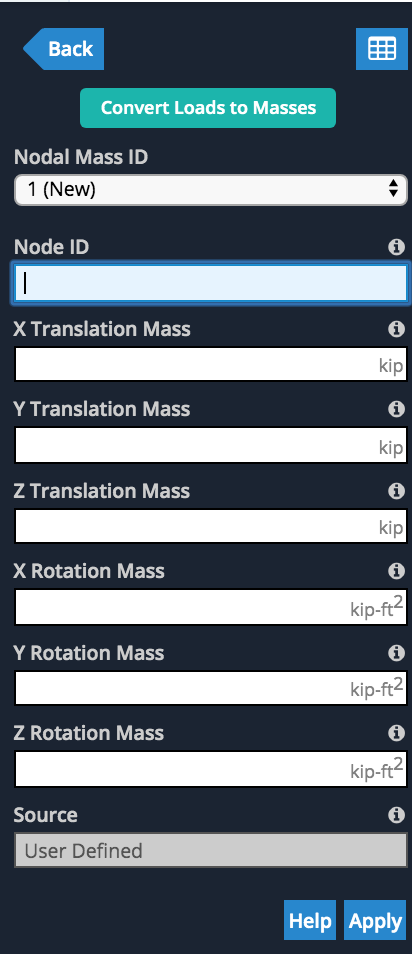
動的周波数分析
SkyCiv動的周波数解析は、構造の最低固有周波数を計算します, 以下の固有値方程式を解くことにより. 静的分析では, システムは時間に依存しないと仮定しています. 動的分析では, 時間依存がある.
動的周波数解析中に、振動下のモード形状と周波数を解決します. 具体的には、振動周波数を解決します (1秒あたりのサイクル) と期間 (1サイクルを完了するのにかかる時間) 構造の各モード形状.
次の式は、周波数解析中に構造3Dによって実行される計算を表します:
[M][U¨]+[K][U]=[0]
[M] = 構造質量行列,
[K] = 構造剛性マトリックス,
[U] = 変位,
[U¨] 時間に関する変位の二階微分です (つまり. 加速度).
ここに, 方程式は解かれません, むしろそれは一般的な固有値問題に還元されます. どこ λ =固有値
[M][U]λ+[K][U]=[0]
結果として得られる固有値は構造の周波数であり、固有ベクトルはモード形状です。. 周波数またはモードが低いほど、1秒あたりのサイクルが少なくなり、発振が遅くなります。.
結果表示
動的周波数分析が完了すると, ユーザーは複数モードの形状の結果を確認できます. モード形状を選択するだけです, そして、構造はモード形状を示すためにアニメーション化します. ユーザーは、構造のすべてのモードの頻度と周期の値も確認できます. これがアニメーションと結果の例です:
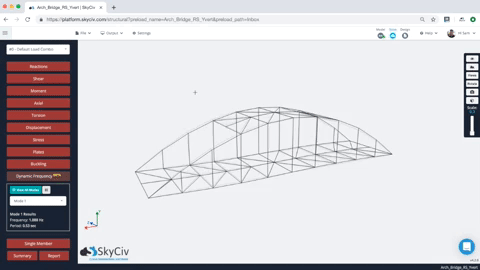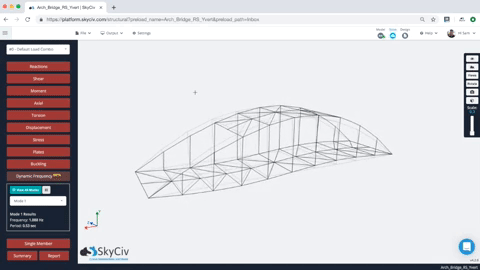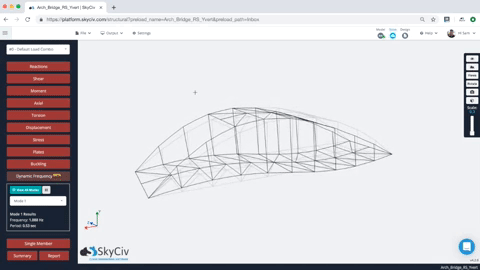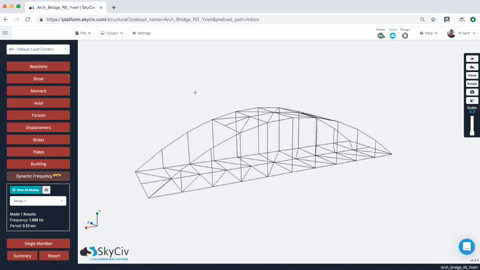
ユーザーには、各モードの結果の一覧表も提供されます, 固有振動数と周期を含む. だから例えば, 上記のモデルには、各結果の頻度と期間があります (簡単にするために注意してください, 最初だけ 10 モードが生成されました – これは以下で制御できます 設定):
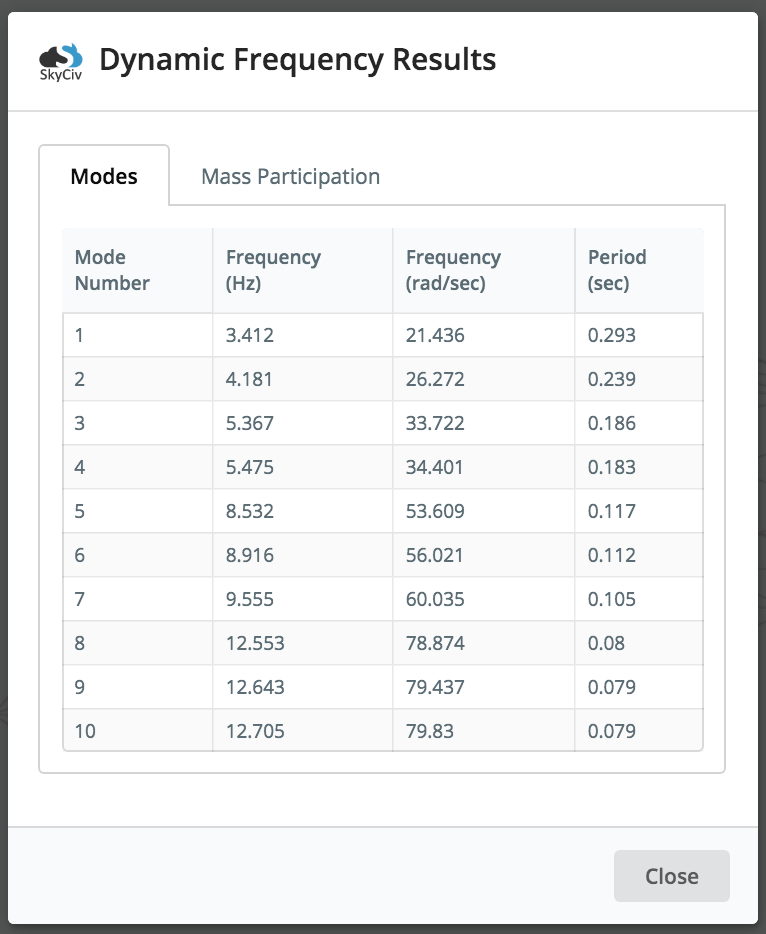
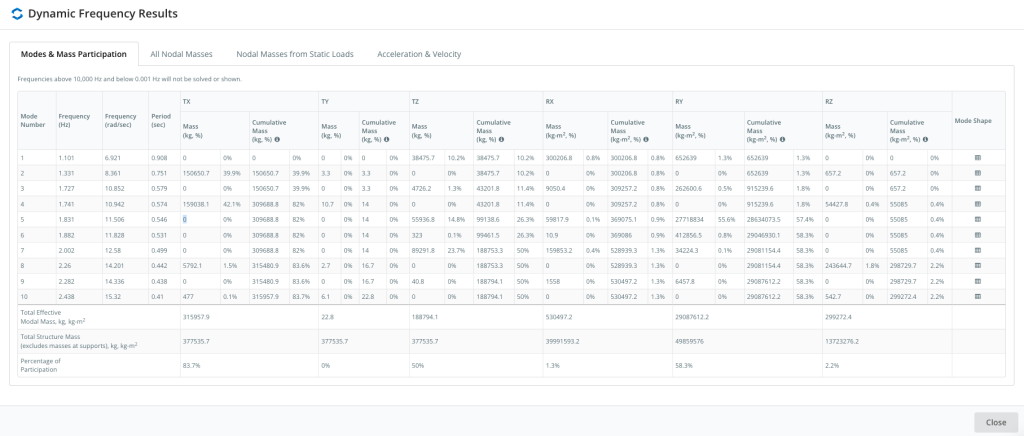
さらに, 構造のモーダルマス参加結果, とそのモードは、 大量参加 タブ. 質量参加係数は、特定の周波数または振動モードに関連する質量の量を表します. 本質的に、ユーザーは、与えられたモードで構造の質量のどれだけが励起されているかを確認できます。. これにより、構造の応答に関する洞察が得られます: マス参加係数が大きいほど, 全体的なレスポンスに対する重要性が大きいほど.
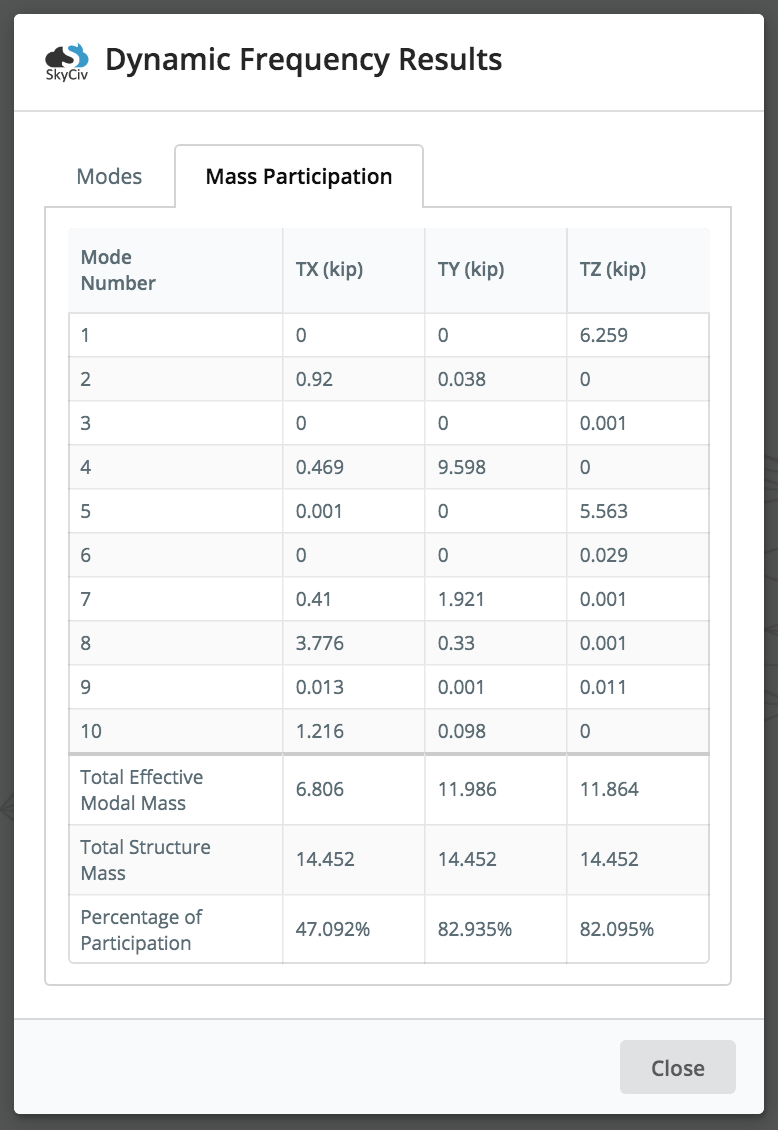
上記のサンプルアニメーションでは (橋の構造), このモードでは、橋がx方向とy方向にのみ移動/振動することがわかります (モード 2), それから, 我々が得る 0 z方向の参加係数 (横向き). 比較的小さな集団参加要因を扱う場合, ユーザーは常に工学的判断を行い、これらの振動モードの影響を分析する必要があります. ほとんどの建築基準法では、少なくとも 90% 分析のための累積質量参加.
