記事上で, ACI-318-19 の最新バージョンを使用して、スラブ設計例を開発します。: “構造コンクリートの建築基準要件,” ACIによって承認された方法によるソフトウェア結果と手計算の比較に焦点を当てた鉄筋コンクリート低層ビルのSkyCivでのモデリングで構成されています: “スラブの直接設計法。” この手順は、建物の主な方向とフレームに沿ったさまざまなストリップに、鉄筋の量とスラブ内の位置を決定するのに便利な要因によって総モーメントを割り当てることから成ります。.
前回の記事を読んでいただければ幸いです, S3D でのプレート設計, SkyCivを使用してプレートのモデリングと設計を紹介する. 検討することをお勧めする別の役立つ情報は、 プレートのモデリング方法? 両方のドキュメントを読み終わったら, 次の完全に機能するスラブの比較例に自由に飛び込んでください!
一般的な建物のレイアウト
次の図は、計算される例の等角図と平面寸法を示しています。. 建物には、柱の支柱の間に梁のない 2 つの高架フラット スラブがあります。.
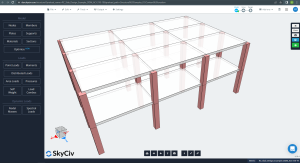
図 1. 建物の例の等角図
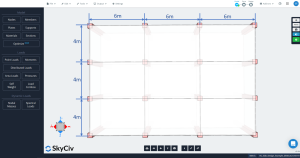
図 2. スラブ平面寸法
二方向スラブの直接設計法 (DDM)
制限事項
ACI 318 DDM を使用して、重力荷重用の鉄筋コンクリート スラブを設計できます。, ジオメトリに従っていくつかの必要条件を収集します, 荷重関係, 対称, 等. これらの制限を次のリストにまとめます。 (PCA ノート):
- “各方向に 3 つ以上の連続するスパンが必要です。”: 図 2 主な方向ごとに 3 つのスパンを示します, 縦と横. OK!
- “スラブ パネルは、長いスパンと短いスパンの比率を持つ長方形でなければなりません (サポートの中心線間) 2以下。”: 図によると 2, 比は等しい \({\フラク{l_1}{4}= frac{6メートル}{4メートル}=1.5 < 2}\). OK!
- “連続スパン長 (サポートの中心線間) 各方向の差を超えてはなりません 1/3 より長いスパンの”. スパン長は各方向とも同じ, 6縦方向に m、横方向に 4 m. OK!
- “列は次の値を超えてオフセットしてはなりません 10% スパンの (オフセット方向) 連続する列の中心線間のいずれかの軸から”. 建物の例には、列にオフセットがありません. OK!
- “荷重は均一に分散する必要があります, ファクタリングされていない、またはサービスのライブ ロードが、ファクタリングされていない、またはサービスのデッド ロードの 2 倍以下である (L/D ≤ 2)”. 各重力荷重の値を取得する, 比率は次のように定義されます \({\フラク{L}{D}= frac{2}{7.8}=0.256 < 2}\). OK!.
- “双方向梁支持スラブ用, 2 つの垂直方向のビームの相対剛性は、コードで指定された最小要件と最大要件を満たさなければなりません。” もう満足; スラブに梁がない. OK!
- “コードによる負のモーメントの再配布は許可されていません。” 例が単純なので, スラブの負のモーメントを再配分する必要はありません. OK!.
縦方向および横方向のストリップの定義
DDM のスラブは、特定のライン グリッドの分析と設計のために 2 つのメイン ストリップに分割する必要があります。: 列と中間のストリップ. 列ストリップの幅は、 \({\フラク {l_1}{4}}\) そして \({\フラク{l_2}{4}}\), どこ \({l_1}\) はライン グリッドに沿ったスパンの長さであり、 \({l_2}\) 横の長さは垂直です.
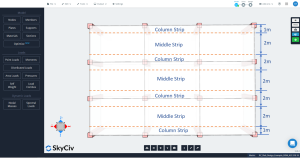
図 3. 縦列と中間ストリップ.
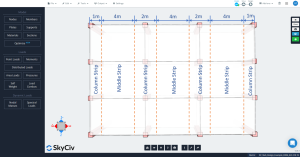
図 4. 横列と中間ストリップ.
最小厚さ
ACI-318 は、式の使用を提案しています: \({t_{分}}= {\フラク{l_n}{30}}={\フラク{6メートル-0.50メートル}{30}}=0.1833m = 0.20m)
予備せん断強度チェック
鉄筋鉄筋を計算する前に, スラブのせん断能力を確認することをお勧めします, 1 つは接続部の直接せん断力用、もう 1 つは接続スラブ柱の打ち抜きせん断力用.
せん断需要を計算するには, 次の重力荷重を使用します:
- 自重スラブ: \({SW={\gamma_c}\回 {t_{スラブ}}={24 {\フラク{kN}{m^3}}}\回 {0.20メートル}=4.8{\フラク{kN}{m^2}} }\)
- 重畳死荷重: \({SD={3 {\フラク{kN}{m^2}}}}\)
- 総死荷重 (SW+SD): \({D={7.8 {\フラク{kN}{m^2}}}}\)
- 活荷重 (住宅占有率) : \({L={2 {\フラク{kN}{m^2}}}}\)
- 考慮された強度荷重 (1.2D+1.6L): \({q_{あなた}={12.56 {\フラク{kN}{m^2}}}}\)
最初のせん断チェックは、 “ビームせん断” タイプ, ここで、次の画像は、総せん断を取得するために考慮される領域を示しています. 各方向を検査します, より広い面積を取る.
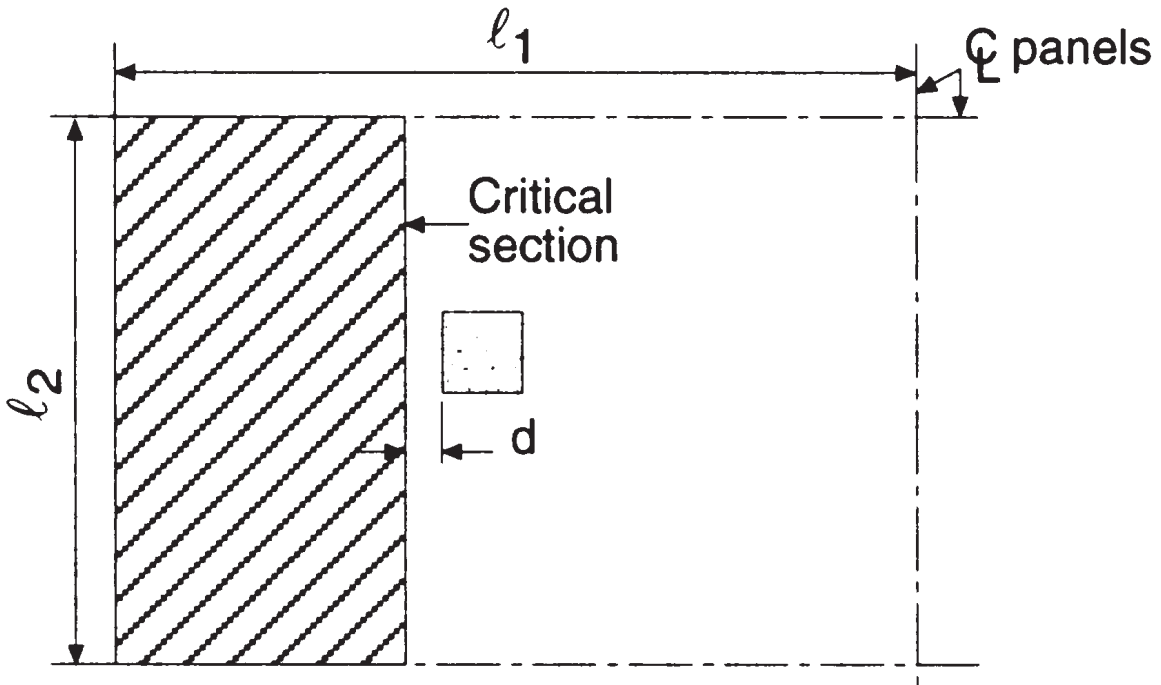
図 5. 柱内部のビームせん断 (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
どこ:
- 縦方向の長さスパン, \({l_1 = 6.0m }\)
- 横方向の長さスパン, \({l_2 = 4.0m}\)
- 総支流面積, 縦方向のせん断 \({A_t = l_2 回 (\フラク{l_1}{2}-\フラク{c_1}{2}-d) = 4.0m 回 (\フラク{6.0メートル}{2}-\フラク{0.50メートル}{2}-0.17メートル) = 10.32 m^2}\) (選択済み)
- 総支流面積, 横方向のせん断, \({A_t = l_1 回 (\フラク{l_2}{2}-\フラク{c_2}{2}-d) = 6.0m 回 (\フラク{4.0メートル}{2}-\フラク{0.50メートル}{2}-0.17メートル) = 9.48 m^2}\)
- 角柱寸法, \({c_1 = c_2 = 0.50m}\)
- 距離d, \({d = h_{スラブ} – カバー = 0.20m – 0.03m = 0.17m }\)
したがって, 内部柱の最大梁せん断は
\({V_u =q_utimes A_t =12.56 {\フラク{kN}{m^2}}\回 10.32 m^2 = 129.62 kN }\)
これをせん断抵抗と比較します, \({\phi_sV_c}\)
- コンクリート強度, \({f'_c = 25 MPa}\)
- 降伏鉄筋強度, \({f_y = 420 MPa}\)
- \({\ファイ_s = 0.75}\)
- \({\phi_sV_c = 0.17phi_s lambda sqrt(f’_c) b_w d; b_w=l_2}\)
\({\phi_sV_c = 0.17回 0.75回 1回sqrt(25 MPa) \回 4000 mm回 170 mm = 433.50 kN }\)
せん断抵抗がせん断需要よりも大きいことがわかります: \({\ファイ_sV_c = 433.50 kN > V_u = 129.62 kN }\) OK!.
以下の画像によると, 内部のスラブと柱の接合部で、打ち抜きせん断力とコンクリートが抵抗する力を計算する必要があります。. 打ち抜きせん断をチェックするコードの意図は、低いせん断応力値を維持することです。.
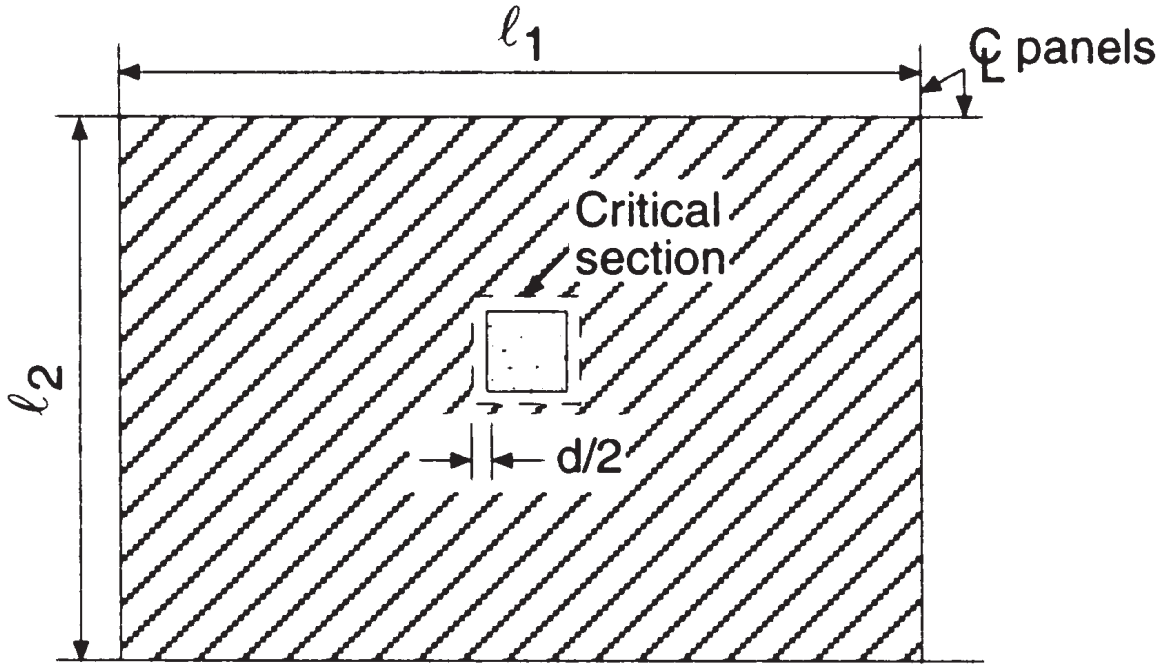
図 6. 内部コラムの双方向せん断 (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
- 総支流面積, パンチングシアー, \({A_t = l_1 times l_2 – (c_1+d)^2 = 6.0m times 4.0m – (0.50m+0.17m)^2 = 23.55 m^2}\) (両方の主方向で同じ面積)
抵抗する総せん断力は
\({V_u =q_utimes A_t =12.56 {\フラク{kN}{m^2}}\回 23.55 m^2 = 295.79 kN }\)
二方向スラブの打ち抜きせん断耐力を求めるには, コード ACI-318 によって確立された経験的方法を使用します。, クリティカル セクションの有効周囲で利用可能な最大せん断応力を考慮する. 内部列のより保守的な式は次のとおりです。
- 打ち抜きせん断能力, \({\phi_sV_c = 0.33phi_s lambda sqrt(f’_c) b_0 日; b_0=4回 (c_1+d)}\)
したがって, せん断抵抗は
\({\phi_sV_c = 0.33回 0.75 \回 1 \平方根(25 MPa) \回 (4\回 (500 mm+170mm)\倍 170mm) = 563.81 kN }\)
せん断抵抗がせん断需要よりも大きいことがわかります: \({\ファイ_sV_c = 563.81 kN > V_u = 295.75 kN }\) OK!.
内部柱接続部での 1 方向および 2 方向のせん断需要を検証しました。. 両方の要求がそれぞれの容量または抵抗よりも小さいため, 次に、スラブの曲げに対する主鉄筋の配筋を計算します。.
あなたがSkyCivで初めての場合, サインアップして自分でソフトウェアをテストする!
スパンあたりの総要素静的モーメント.
二重固定端ビームに展開できる最大モーメントは、に等しいアイソスタティック モーメントです。 \({M = frac{w回 {l_1}^ 2}{8}}\) (図を参照 6).
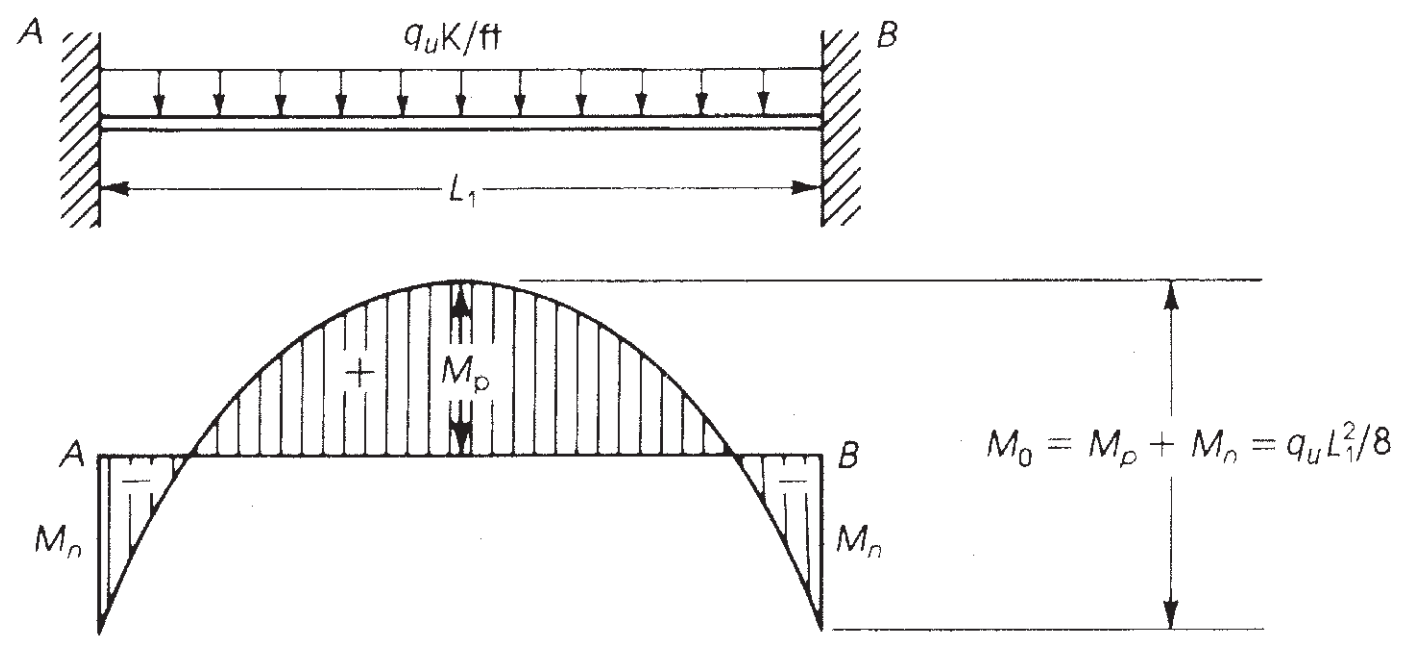
図 7. 固定端ビームの曲げモーメント. (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
ACI-18 はこの原則を採用し、, 直接設計法の場合 (DDM), スパンごとに考慮される最大静的モーメントを確立します \({M_0}\)
縦方向:
- \({M_0 = frac {q_utimes l_2times {l_{ん,1}}^ 2}{8}}\)
- \({M_0 = frac {12.56 {\フラク{kN}{m^2}}\回 4.0m回 (6メートル-0.50メートル)^ 2}{8}=189.97kN-m}\)
横方向:
- \({M_0 = frac {q_utimes l_1times {l_{ん,2}}^ 2}{8}}\)
- \({M_0 = frac {12.56 {\フラク{kN}{m^2}}\回 6.0m回 (4メートル-0.50メートル)^ 2}{8}=115.40kN-m}\)
次のステップは、パネルのタイプを考慮して、この総モーメントを割り当てることです, 内装または外装. (図を参照 7). その後, スパンが連続しているため, 瞬間もプラスとマイナスに分ける必要がある. このラストは画像で示されています 8 そして 9.
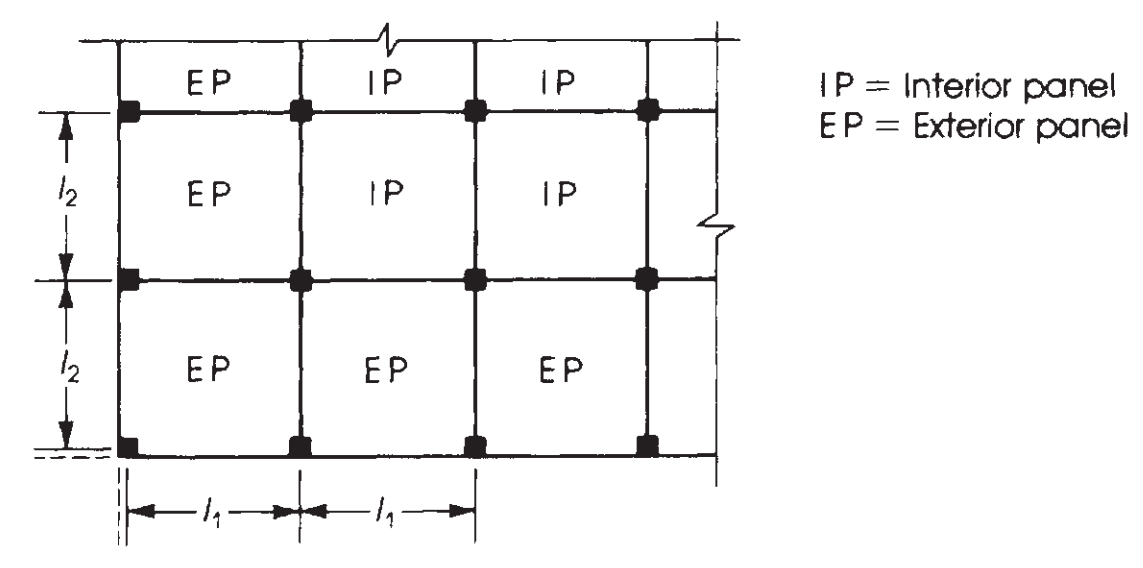
図 8. スラブ プラン内の相対的な位置に応じたパネルの定義. (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
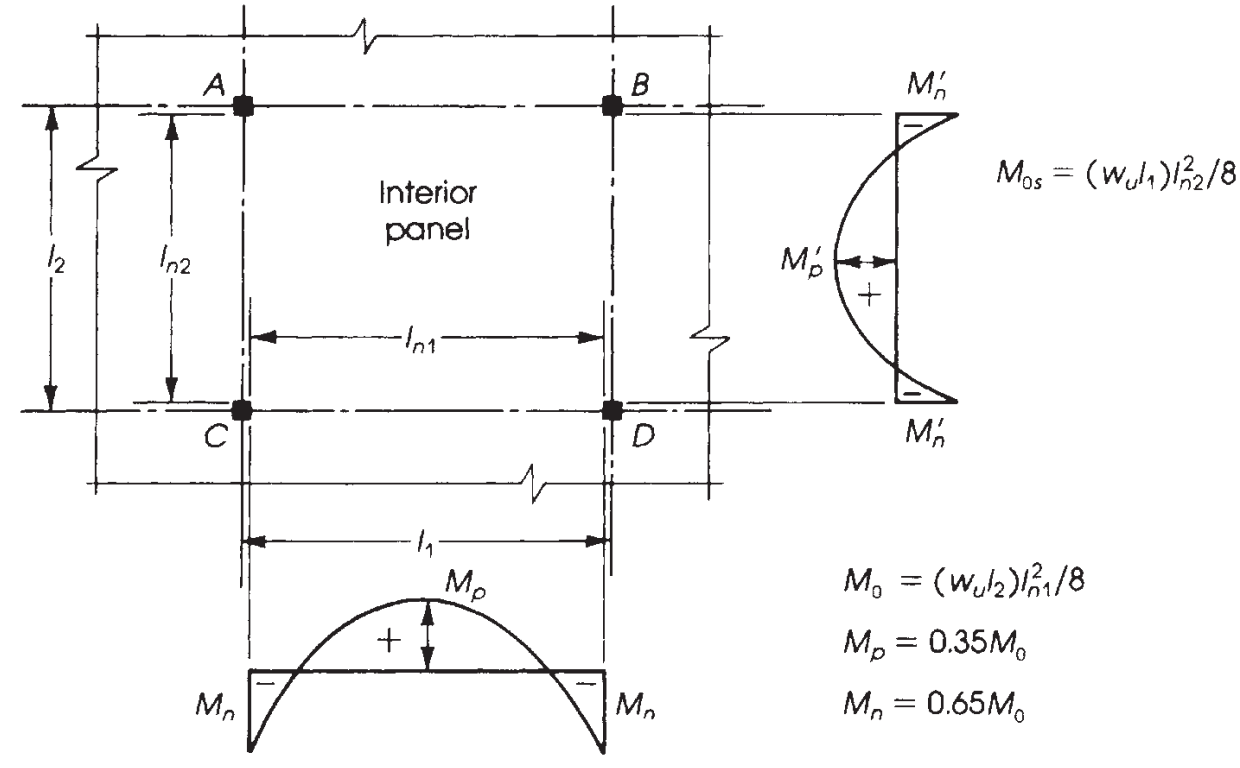
図 9. 内装パネルのモーメント分布. (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
設計しているスラブに応じて、モーメントの正しい分布を知ることが重要です. この例では, 次の画像に最後のケースがあります (図 9), “ビームなし,” 梁のないフラット スラブまたはソリッド スラブに適用される, エッジでもサポート間でもない.
図に示す 5 つのケースの主な違い 9 外部パネルに割り当てられるモーメント分数です。, 最後の相対拘束によって計算される値が変化する.
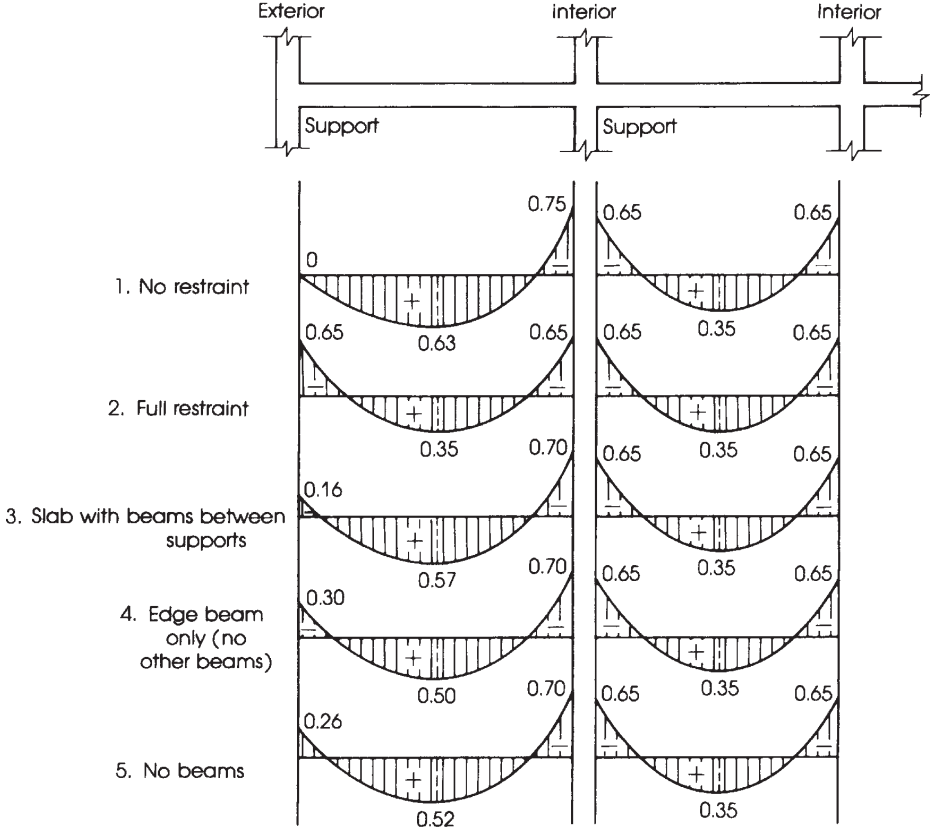
図 10. 負および正のスパン モーメントへの総静的モーメントの分布. (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
合計因数モーメントの分布 \({M_0}\) スパンごとに負の瞬間と正の瞬間に.
一度 \({M_0}\) 計算済み, 各デザイン ストリップでモーメントの割合を正と負に割り当てる時が来ました, あれは, 列と中間のストリップ. より明確にするために, 図 10 合計モーメントの分布で考慮すべき適切な要因を指定するのに役立ちます.
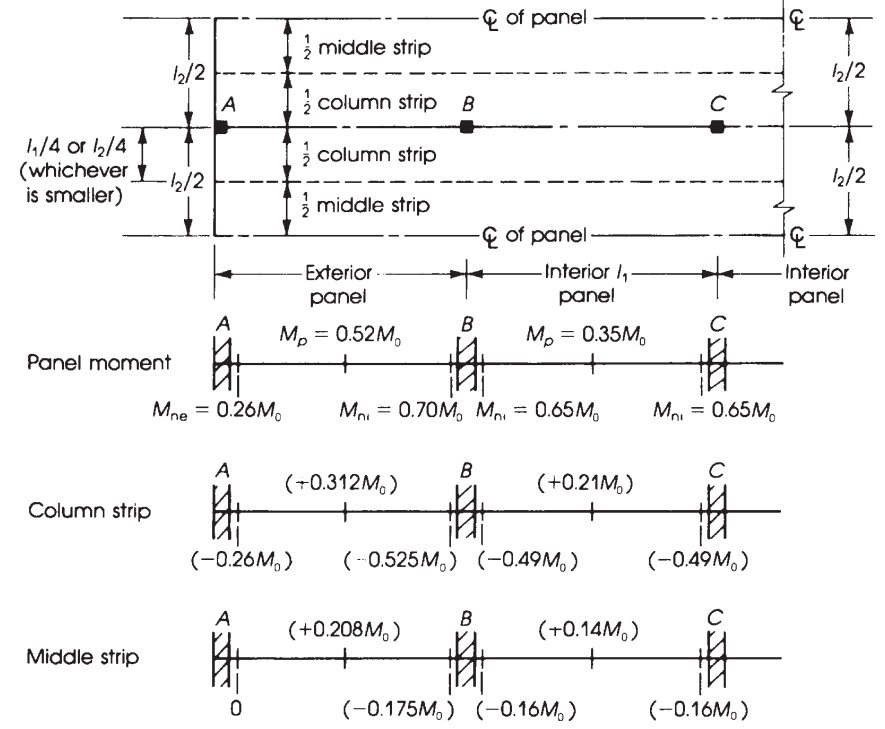
図 11. 等価ラーメンの幅と平面スラブのモーメント分布. (Nadim Hassoun と Akthem AI-Manaseer, “構造コンクリートの理論と設計”)
図に示されている以前の要因を使用して 10, 次の表で最終的な瞬間を取得します.
縦方向: \({M_0 = 189.97 kN-m}\)
| スパン (ES:外観, IS:インテリア) | 総モーメント (kN-m) | コラムストリップモーメント (kN-m) | ミドルストリップモーメント (kN-m) |
|---|---|---|---|
| エクステリア ネガティブES | 0.26M0=49.39 | 0.26M0=49.39 | 0 |
| 正の ES | 0.52M0=98.78 | 0.31M0=58.89 | 0.21M0=39.89 |
| 内部負ES | 0.70M0=132.98 | 0.53M0=100.68 | 0.17M0=32.29 |
| ポジティブIS | 0.35M0=66.49 | 0.21M0=39.89 | 0.14M0=26.60 |
| ネガティブIS | 0.65M0=123.48 | 0.49M0=93.09 | 0.16M0=30.40 |
一度配信した瞬間と, スラブに配置する鉄筋補強材を決定する時が来ました. 計算を 1 つだけ展開し、すべての結果を表にまとめます。.
列ストリップの外部負スパンのモーメント, \({M_u = 49.39 kN-m}\)
- 想定張力制御区間. \({\ファイ_f = 0.9}\)
- 列ストリップ幅, \({b=2.0m}\)
- 鉄筋エリア, \({A_s = frac{ムー}{\phi_ftimes 0.9dtimes fy}= frac{49.39kN-m}{0.9\回 0.9(0.17メートル)\回 420 MPa}=853.996 {んん}^ 2}\)
- \({\曲げモーメントは、セクションで各方向に計算されます{分} = 0.0018}\). 鉄骨最小補強面積, \({A_{s,分}=rho_{分}\回 b回 d = 0.0018 \倍 2.0m 回 0.17m =612 {んん}^ 2}\). 今, セクションが張力制御として動作しているかどうかを確認します.
- \({a = frac{A_stimes f_y}{0.85\回f'c回b} = frac{853.996 {んん}^2回 420 MPa}{0.85\回 25 MPa回 2.0m }= 8.439 んん}\)
- \({c = frac{a}{\beta_1}= frac{8.439 んん}{0.85} = 9.929mm }\)
- \({\varepsilon_t = (\フラク{0.003}{c})\倍d – 0.003 = (\フラク{0.003}{9.929んん})\倍 170mm – 0.003 = 0.048 > 0.005 }\) OK!, テンションコントロールセクションです!.
| スパン(ES:外観, IS:インテリア) | コラムストリップモーメント (kN-m) | \({A_{s,計算} ({んん}^ 2)}\) | \({A_{s,分} ({んん}^ 2)}\) | \({a (んん)}\) | \({c (んん)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| エクステリア ネガティブES | 49.39 | 853.996 | 612.0 | 8.439 | 9.929 | 0.048 > 0.005! |
| 正の ES | 58.89 | 1018.259 | 612.0 | 10.063 | 11.839 | 0.040 > 0.005! |
| 内部負ES | 100.68 | 1740.844 | 612.0 | 17.204 | 20.24 | 0.022 > 0.005! |
| ポジティブIS | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.06 > 0.005! |
| ネガティブIS | 93.09 | 1609.607 | 612.0 | 15.907 | 18.714 | 0.024 > 0.005! |
中央ストリップの外部正スパンのモーメント, \({M_u = 39.89 kN-m}\)
- 想定張力制御区間. \({\ファイ_f = 0.9}\)
- 中間ストリップ幅, \({b=2.0m}\)
- 鉄筋エリア, \({A_s = frac{ムー}{\phi_ftimes 0.9dtimes fy}= frac{39.89kN-m}{0.9\回 0.9(0.17メートル)\回 420 MPa}=689.733 {んん}^ 2}\)
- \({\曲げモーメントは、セクションで各方向に計算されます{分} = 0.0018}\). 鉄骨最小補強面積, \({A_{s,分}=rho_{分}\回 b回 d = 0.0018 \倍 2.0m 回 0.17m =612 {んん}^ 2}\). 今, セクションが張力制御として動作しているかどうかを確認します.
- \({a = frac{A_stimes f_y}{0.85\回f'c回b} = frac{689.766 {んん}^2回 420 MPa}{0.85\回 25 MPa回 2.0m }= 6.816 んん}\)
- \({c = frac{a}{\beta_1}= frac{6.816 んん}{0.85} = 8.019 んん }\)
- \({\varepsilon_t = (\フラク{0.003}{c})\倍d – 0.003 = (\フラク{0.003}{8.019んん})\倍 170mm – 0.003 = 0.0605 > 0.005 }\) OK!, テンションコントロールセクションです!.
| スパン(ES:外観, IS:インテリア) | ミドルストリップモーメント (kN-m) | \({A_{s,計算} ({んん}^ 2)}\) | \({A_{s,分} ({んん}^ 2)}\) | \({a (んん)}\) | \({c (んん)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| エクステリア ネガティブES | 0 | 0.00 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正の ES | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.061 > 0.005! |
| 内部負ES | 32.29 | 558.322 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| ポジティブIS | 26.60 | 459.937 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| ネガティブIS | 30.40 | 525.642 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
横方向: \({M_0 = 115.40 kN-m}\)
| スパン (ES:外観, IS:インテリア) | 総モーメント (kN-m) | コラムストリップモーメント (kN-m) | ミドルストリップモーメント (kN-m) |
|---|---|---|---|
| エクステリア ネガティブES | 0.26M0=30.00 | 0.26M0=30.00 | 0 |
| 正の ES | 0.52M0=60.00 | 0.31M0=35.77 | 0.21M0=24.23 |
| 内部負ES | 0.70M0=80.78 | 0.53M0=61.16 | 0.17M0=19.62 |
| ポジティブIS | 0.35M0=40.39 | 0.21M0=24.23 | 0.14M0=16.16 |
| ネガティブIS | 0.65M0=75.01 | 0.49M0=56.55 | 0.16M0=18.46 |
一度配信した瞬間と, スラブに配置する鉄筋補強材を決定する時が来ました. 計算を 1 つだけ展開し、すべての結果を表にまとめます。.
列ストリップの外部負スパンのモーメント, \({M_u = 30.00 kN-m}\)
- 想定張力制御区間. \({\ファイ_f = 0.9}\)
- 列ストリップ幅, \({b=2.0m}\)
- 鉄筋エリア, \({A_s = frac{ムー}{\phi_ftimes 0.9dtimes fy}= frac{30.00kN-m}{0.9\回 0.9(0.17メートル)\回 420 MPa}=518.726 {んん}^ 2}\)
- \({\曲げモーメントは、セクションで各方向に計算されます{分} = 0.0018}\). 鉄骨最小補強面積, \({A_{s,分}=rho_{分}\回 b回 d = 0.0018 \倍 2.0m 回 0.17m =612 {んん}^ 2}\). 今, セクションが張力制御として動作しているかどうかを確認します.
- \({a = frac{A_stimes f_y}{0.85\回f'c回b} = frac{518.726 {んん}^2回 420 MPa}{0.85\回 25 MPa回 2.0m }= 6.048 んん}\)
- \({c = frac{a}{\beta_1}= frac{6.048 んん}{0.85} = 7.115mm }\)
- \({\varepsilon_t = (\フラク{0.003}{c})\倍d – 0.003 = (\フラク{0.003}{7.115んん})\倍 170mm – 0.003 = 0.069 > 0.005 }\) OK!, テンションコントロールセクションです!.
| スパン(ES:外観, IS:インテリア) | コラムストリップモーメント (kN-m) | \({A_{s,計算} ({んん}^ 2)}\) | \({A_{s,分} ({んん}^ 2)}\) | \({a (んん)}\) | \({c (んん)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| エクステリア ネガティブES | 30.00 | 518.726 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正の ES | 35.77 | 618.494 | 612.0 | 6.112 | 7.191 | 0.068 > 0.005! |
| 内部負ES | 61.16 | 1057.509 | 612.0 | 10.451 | 12.295 | 0.038 > 0.005! |
| ポジティブIS | 24.23 | 418.958 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| ネガティブIS | 56.55 | 977.799 | 612.0 | 9.663 | 11.368 | 0.042 > 0.005! |
中央ストリップの外部正スパンのモーメント, \({M_u = 24.23 kN-m}\)
- 想定張力制御区間. \({\ファイ_f = 0.9}\)
- 列ストリップ幅, \({b=4.0m}\)
- 鉄筋エリア, \({A_s = frac{ムー}{\phi_ftimes 0.9dtimes fy}= frac{24.23 kN-m}{0.9\回 0.9(0.17メートル)\回 420 MPa}=418.958 {んん}^ 2}\)
- \({\曲げモーメントは、セクションで各方向に計算されます{分} = 0.0018}\). 鉄骨最小補強面積, \({A_{s,分}=rho_{分}\回 b回 d = 0.0018 \倍 4.0m 回 0.17m =1224 {んん}^ 2}\). 今, セクションが張力制御として動作しているかどうかを確認します.
- \({a = frac{A_stimes f_y}{0.85\回f'c回b} = frac{1224 {んん}^2回 420 MPa}{0.85\回 25 MPa回 4.0m }= 6.048 んん}\)
- \({c = frac{a}{\beta_1}= frac{6.048 んん}{0.85} = 7.115 んん }\)
- \({\varepsilon_t = (\フラク{0.003}{c})\倍d – 0.003 = (\フラク{0.003}{7.115んん})\倍 170mm – 0.003 = 0.069 > 0.005 }\) OK!, テンションコントロールセクションです!.
| スパン(ES:外観, IS:インテリア) | ミドルストリップモーメント (kN-m) | \({A_{s,計算} ({んん}^ 2)}\) | \({A_{s,分} ({んん}^ 2)}\) | \({a (んん)}\) | \({c (んん)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| エクステリア ネガティブES | 0.00 | 0.00 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正の ES | 24.23 | 418.958 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| 内部負ES | 19.62 | 339.247 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| ポジティブIS | 16.16 | 279.420 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| ネガティブIS | 18.46 | 319.189 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
あなたがSkyCivで初めての場合, サインアップして自分でソフトウェアをテストする!
SkyCiv S3D 設計モジュール
このセクションで, SkyCivに含まれるプレート設計用モジュールを使用して設計結果を記述します. 構造をモデル化して分析する方法を説明していません (これらのために, ドキュメントでこのトピックに関する関連記事を参照してください: SkyCivで構造をモデル化する方法?, 建物モデルに荷重を適用する方法? そして 線形弾性解析の実行方法?)
正確な設計結果を得るために、スラブに細かいメッシュを適用すると便利です. より明確にするために、次の画像を見てください.
図 12. スラブに適用されるより細かいメッシュ
次のステップは、設計モジュールを実行し、最適化された鉄筋面積を計算するオプションを選択することです.
図 13. 設計最適化前のスラブ コンクリート プロパティの定義.
図 14 プレートのローカル軸の向きを表します. ローカル軸なので 3 下向きです, の “上” 底です, そしてその “底” トップになります, したがって、設計からデータを正しく取得します.
もう 1 つの重要な事実は、スラブ メッシュ サイズです。; 平面寸法が 500mm x 500mm のプレート スクエア エレメントです。. SkyCiv S3Dは、有限要素ごとの統合値として補強面積を与えます. したがって, 柱または中間ストリップの総鉄筋面積を取得する場合, 分析対象のストリップ幅を合計した要素数から平均値を計算する必要があります. 例えば, 列ストリップ用, 4つの要素が考慮されます (4×0.5m = 2m).
図 14. スラブの例におけるローカル軸の向き.
最初, 軸の縦方向に沿って必要な補強面積を分析します 1.
列ストリップ
- 外装マイナスモーメント (トップ補強): \({A_{s,上} =(119.09\回 2 + 952.72 + 833.64 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 1012.27 {んん}^ 2}\)
- 外装プラスモーメント (底補強): \({A_{s,ボット} = 4*463.90 \フラク{{んん}^ 2}{メートル}\倍 0.50m = 927.80 {んん}^ 2}\)
- エクステリア インテリア マイナスモーメント (トップ補強): \({A_{s,上} =(1071.82\回 2 +714.54 \回 2 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 1786.36 {んん}^ 2}\)
- インテリアポジティブモーメント(底補強): \({A_{s,ボット} = 4*309.27 \フラク{{んん}^ 2}{メートル}\倍 0.50m = 618.54 {んん}^ 2}\)
- 内部負モーメント (トップ補強): \({A_{s,上} =(714.54\回 2 +952.73 \回 2 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 1667.27 {んん}^ 2}\)
ミドルストリップ
- 外装マイナスモーメント (トップ補強): \({A_{s,上} =(119.09\回 4)\フラク{{んん}^ 2}{メートル} \倍 0.50m = 238.18 {んん}^ 2}\)
- 外装プラスモーメント (底補強): \({A_{s,ボット} = (463.90\回 2 +412.36 \回 2 ) \フラク{{んん}^ 2}{メートル}\倍 0.50m = 876.26 {んん}^ 2}\)
- エクステリア インテリア マイナスモーメント (トップ補強): \({A_{s,上} =(357.27\回 2 +476.36 \回 2 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 833.63 {んん}^ 2}\)
- インテリアポジティブモーメント(底補強): \({A_{s,ボット} = 4*257.72 \フラク{{んん}^ 2}{メートル}\倍 0.50m = 515.44 {んん}^ 2}\)
- 内部負モーメント (トップ補強): \({A_{s,上} =(357.27\回 2 +476.36 \回 2 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 833.63 {んん}^ 2}\)
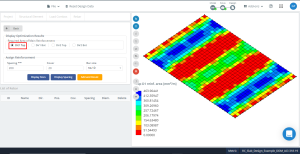
図 15. 方向の最適化結果 “1” そして上側 (底部側, 実際に).
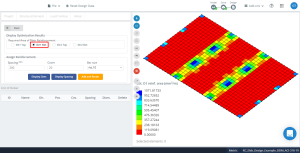
図 16. 方向の最適化結果 “1” そして下側 (上面, 実際に).
最後に, 軸の横方向に沿って必要な補強面積を分析します 2.
列ストリップ
- 外装マイナスモーメント (トップ補強): \({A_{s,上} =(91.55\回 2 + 457.73 + 549.28 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 595.055 {んん}^ 2}\)
- 外装プラスモーメント (底補強): \({A_{s,ボット} = (269.68\回 3+239.72) \フラク{{んん}^ 2}{メートル}\倍 0.50m = 524.38 {んん}^ 2}\)
- エクステリア インテリア マイナスモーメント (トップ補強): \({A_{s,上} =(823.92\回 2 +549.28 +457.73)\フラク{{んん}^ 2}{メートル} \倍 0.50m = 1327.43 {んん}^ 2}\)
- インテリアポジティブモーメント(底補強): \({A_{s,ボット} = (179.79\回 3+149.82) \フラク{{んん}^ 2}{メートル}\倍 0.50m = 344.60 {んん}^ 2}\)
- 内部負モーメント (トップ補強): \({A_{s,上} =(823.92\回 2 +549.28 +457.73)\フラク{{んん}^ 2}{メートル} \倍 0.50m = 1327.43 {んん}^ 2}\)
ミドルストリップ
- 外装マイナスモーメント (トップ補強): \({A_{s,上} =(183.09\倍 2+91.55回 6)\フラク{{んん}^ 2}{メートル} \倍 0.50m = 457.74 {んん}^ 2}\)
- 外装プラスモーメント (底補強): \({A_{s,ボット} = (209.75\回 2 +179.79 \回 2 +149.82 \回 4) \フラク{{んん}^ 2}{メートル}\倍 0.50m = 689.18{んん}^ 2}\)
- エクステリア インテリア マイナスモーメント (トップ補強): \({A_{s,上} =(274.64\倍 2+91.55回 6)\フラク{{んん}^ 2}{メートル} \倍 0.50m = 549.29 {んん}^ 2}\)
- インテリアポジティブモーメント(底補強): \({A_{s,ボット} = (119.86\回 4 + 89.89\回 4) \フラク{{んん}^ 2}{メートル}\倍 0.50m = 419.50 {んん}^ 2}\)
- 内部負モーメント (トップ補強): \({A_{s,上} =(274.64\倍 2+91.55回 6 )\フラク{{んん}^ 2}{メートル} \倍 0.50m = 549.29 {んん}^ 2}\)
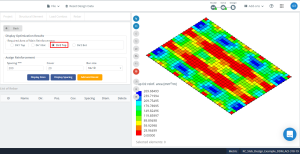
図 17. 方向の最適化結果 “2” そして上側 (底部側, 実際に).
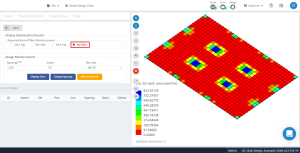
図 18. 方向の最適化結果 “2” そして下側 (上面, 実際に).
結果比較
次の表は、DDM の結果を示しています。 (“直接設計法”) S3D鉄筋の最適化.
| スパン (ES:外観, IS:インテリア) | 列ストリップ (S3D 設計) \({として ({んん}^ 2)}\) | 列ストリップ (ACI-318 DDM) \({として ({んん}^ 2)}\) | % 差分 | ミドルストリップ (S3D 設計) \({として ({んん}^ 2)}\) | ミドルストリップ (ACI-318 DDM) \({として ({んん}^ 2)}\) | % 差分 |
|---|---|---|---|---|---|---|
| エクステリア ネガティブES | 1012.27 | 853.996 | 15.636 | 238.18 | 0 (612.0) | 100.00 |
| 正の ES | 927.80 | 1018.259 | 9.75 | 876.26 | 689.733 | 21.287 |
| 内部負ES | 1786.36 | 1740.844 | 2.48 | 833.63 | 558.322 (612.0) | 26.586 |
| ポジティブIS | 618.54 | 689.733 | 11.51 | 515.44 | 459.937 (612.0) | 18.734 |
| ネガティブIS | 1667.27 | 1609.607 | 3.459 | 833.63 | 525.642 (612.0) | 26.586 |
横方向
| スパン (ES:外観, IS:インテリア) | 列ストリップ (S3D 設計) \({として ({んん}^ 2)}\) | 列ストリップ (ACI-318 DDM) \({として ({んん}^ 2)}\) | % 差分 | ミドルストリップ (S3D 設計) \({として ({んん}^ 2)}\) | ミドルストリップ (ACI-318 DDM) \({として ({んん}^ 2)}\) | % 差分 |
|---|---|---|---|---|---|---|
| エクステリア ネガティブES | 595.055 | 518.726 | 12.827 | 457.74 | 0 (1224) | 100.00 |
| 正の ES | 524.38 | 618.494 | 17.948 | 689.18 | 418.958 | 39.209 |
| 内部負ES | 1327.43 | 1057.509 | 20.334 | 549.29 | 339.247 | 38.239 |
| ポジティブIS | 344.60 | 418.958 | 21.578 | 419.50 | 279.42 | 33.392 |
| ネガティブIS | 1327.43 | 977.799 | 26.339 | 549.29 | 319.189 | 41.891 |
結論
この記事では、プレート設計用のSkyCivモジュールがコードACI-318-19に従って曲げスラブの鉄筋を計算することを示しました. 列ストリップでの分析結果の比較, 相対的な剛性のため, 瞬間は非常に集中しています, 手計算と S3D による最適化の違いは、次の値を丸めます。 10 – 15%. この実用性は、解析手順と設計手順が見事に一致していることを示しています.
ミドルストリップ用, コードは対応する列ストリップを取得した後の残りの部分のみを割り当てるため、結果はもう少し異なります. これは、ソフトウェアからの分析と比較すると、試合に影響を与えます, どちらがより正確です.
SkyCivの新機能? サインアップして自分でソフトウェアを試す!


